Class 8 RD Sharma Solutions- Chapter 16 Understanding Shapes Quadrilaterals – Exercise 16.1 | Set 2
Last Updated :
08 Apr, 2021
Question 13. In Figure, find the measure of ∠MPN.
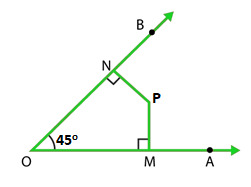
Solution:
As we know that Sum of angles of a quadrilateral is = 360°
In the quadrilateral MPNO
∠NOP = 45°, ∠OMP = ∠PNO = 90° (Given)
Let us assume that angle ∠MPN is x°
∠NOP + ∠OMP + ∠PNO + ∠MPN = 360°
45° + 90° + 90° + x° = 360°
x° = 360° – 225°
x° = 135°
Hence, Measure of ∠MPN is 135°
Question 14. The sides of a quadrilateral are produced in order. What is the sum of the four exterior angles?
Solution:
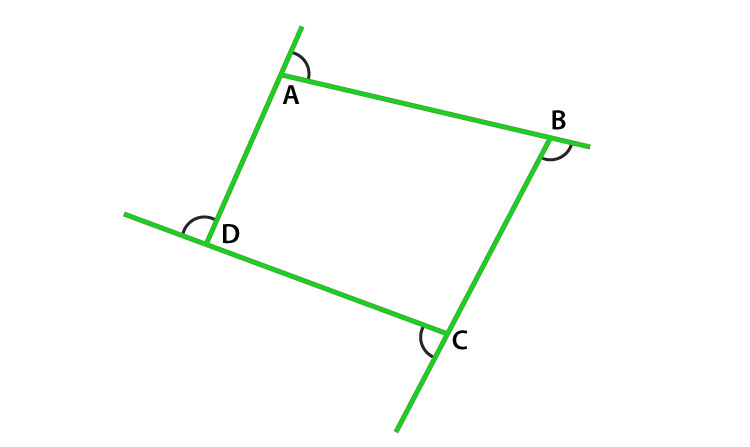
As we know that, exterior angle + interior adjacent angle = 180° (Linear pair)
Applying relation for polygon having n sides
Sum of all exterior angles + Sum of all interior angles = n × 180°
Sum of all exterior angles = n × 180° – Sum of all interior angles
= n × 180° – (n -2) × 180° (Sum of interior angles is = (n – 2) x 180°)
= n × 180° – n × 180° + 2 × 180°
= 180°n – 180°n + 360° = 360°
Hence, Sum of four exterior angles is 360o
Question 15. In Figure, the bisectors of ∠A and ∠B meet at a point P. If ∠C =100° and ∠D = 50°, find the measure of ∠APB.
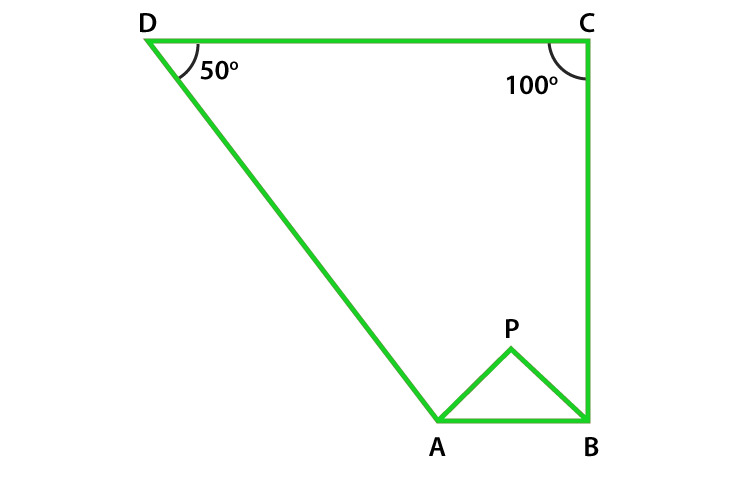
Solution:
As we know that Sum of angles of a quadrilateral is = 360°
In the quadrilateral ABCD
Given that,
∠C =100° and ∠D = 50°
∠A + ∠B + ∠C + ∠D = 360o
∠A + ∠B + 100o + 50o = 360o
∠A + ∠B = 360o – 150o
∠A + ∠B = 210o (Equation 1)
Now in Δ APB
½ ∠A + ½ ∠B + ∠APB = 180o (sum of triangle is 180o)
∠APB = 180o – ½ (∠A + ∠B) (Equation 2)
On substituting value of ∠A + ∠B = 210 from equation (1) in equation (2)
∠APB = 180o – ½ (210o)
= 180o – 105o = 75o
Hence, the measure of ∠APB is 75o.
Question 16. In a quadrilateral ABCD, the angles A, B, C and D are in the ratio 1:2:4:5. Find the measure of each angle of the quadrilateral.
Solution:
As we know that Sum of angles of a quadrilateral is = 360°
Let each angle be xo
Therefore,
xo + 2xo + 4xo + 5xo = 360o
12xo = 360o
xo = 360o/12 = 30o
Value of angles are as x = 30o,
2x = 2 × 30 = 60o
4x = 4 × 30 = 120o
5x = 5 × 30 = 150o
Hence, Value of angles are 30o, 60o, 120o, 150o.
Question 17. In a quadrilateral ABCD, CO and DO are the bisectors of ∠C and ∠D respectively. Prove that ∠COD = 1/2 (∠A +∠B).
Solution:
As we know that sum of angles of a quadrilateral is 360°
In the quadrilateral ABCD
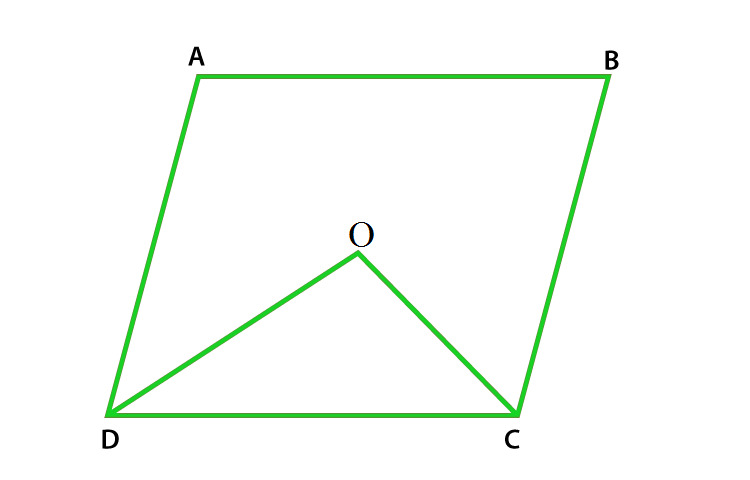
Therefore,
∠A + ∠B + ∠C + ∠D = 360o
∠A + ∠B = 360o – (∠C + ∠D)
½ (∠A + ∠B) = ½ [360o – (∠C + ∠D)]
= 180o – ½ (∠C + ∠D) (Equation 1)
Now in Δ DOC
½ ∠D + ½ ∠C + ∠COD = 180o (We know that sum of triangle = 180o)
½ (∠C + ∠D) + ∠COD = 180o
∠COD = 180o – ½ (∠C + ∠D) (Equation 2)
In equations (1) and (2) RHS is equal then LHS will also equal.
Hence, ∠COD = ½ (∠A + ∠B) is proved.
Question 18. Find the number of sides of a regular polygon, when each of its angles has a measure of
(i) 160°
(ii) 135°
(iii) 175°
(iv) 162°
(v) 150°
Solution:
The sum of interior angle A of a polygon of n sides is given by A = [(n-2) ×180o] /n
(i) 160o
Angle of quadrilateral is 160° (Given)
160o = [(n-2) ×180o]/n
160on = (n-2) ×180o
160on = 180on – 360o
180on – 160on = 360o
20on = 360o
n = 360o/20 = 18
Hence Number of sides are 18
(ii) 135o
Angle of quadrilateral is 135° (Given)
135o = [(n-2) ×180o]/n
135on = (n-2) ×180o
135on = 180on – 360o
180on – 135on = 360o
45on = 360o
n = 360o / 45 = 8
Hence Number of sides are 8
(iii) 175o
Angle of quadrilateral is 175° (Given)
175o = [(n-2) ×180o]/n
175on = (n-2) ×180o
175on = 180on – 360o
180on – 175on = 360o
5on = 360o
n = 360o/5 = 72
Hence Number of sides are 72
(iv) 162o
Angle of quadrilateral is 162° (Given)
162o = [(n-2) ×180o]/n
162on = (n-2) ×180o
162on = 180on – 360o
180on – 162on = 360o
18on = 360o
n = 360o/18 = 20
Hence Number of sides are 20
(v) 150o
Angle of quadrilateral is 160° (Given)
150o = [(n-2) ×180o]/n
150on = (n-2) ×180o
150on = 180on – 360o
180on – 150on = 360o
30on = 360o
n = 360o/30 = 12
Hence Number of sides are 12
Question 19. Find the numbers of degrees in each exterior angle of a regular pentagon.
Solution:
As we know that the sum of exterior angles of a polygon is 360°
Sum of each exterior angle of a polygon = 360o/n (n is the number of sides)
As we know that number of sides in a pentagon is 5
Sum of each exterior angle of a pentagon = 360o/5 = 72o
Hence Measure of each exterior angle of a pentagon is 72o
Question 20. The measure of angles of a hexagon are x°, (x-5)°, (x-5)°, (2x-5)°, (2x-5)°, (2x+20)°. Find value of x.
Solution:
As we know that the sum of interior angles of a polygon = (n – 2) × 180° (n = number of sides of polygon)
As we know that hexagon has 6 sides therefore,
The sum of interior angles of a hexagon = (6 – 2) × 180° = 4 × 180° = 720°
x°+ (x-5)°+ (x-5)°+ (2x-5)°+ (2x-5)°+ (2x+20)° = 720°
x°+ x°- 5°+ x° – 5°+ 2x° – 5°+ 2x° – 5°+ 2x° + 20° = 720°
9x° = 720°
x = 720o/9 = 80o
Hence Value of x is 80o
Question 21. In a convex hexagon, prove that the sum of all interior angle is equal to twice the sum of its exterior angles formed by producing the sides in the same order.
Solution:
As we know that the sum of interior angles of a polygon = (n – 2) × 180°
The sum of interior angles of a hexagon = (6 – 2) × 180° = 4 × 180° = 720°
Sum of exterior angle of a polygon is 360°
Hence Sum of interior angles of a hexagon = Twice the sum of interior angles.
Hence proved.
Question 22. The sum of the interior angles of a polygon is three times the sum of its exterior angles. Determine the number of sides of the polygon.
Solution:
As we know that the sum of interior angles of a polygon = (n – 2) × 180° (i)
The Sum of exterior angle of a polygon is 360°
therefore,
Sum of Interior Angles = 3 × sum of exterior angles
= 3 × 360° = 1080° (ii)
Now by equating (i) and (ii) we get,
(n – 2) × 180° = 1080°
n – 2 = 1080o/180o
n – 2 = 6
n = 6 + 2 = 8
Hence Number of sides of a polygon is 8.
Question 23. Determine the number of sides of a polygon whose exterior and interior angles are in the ratio 1 : 5.
Solution:
As we know that the sum of interior angles of a polygon = (n – 2) × 180° (i)
The Sum of exterior angle of a polygon is 360°
As we know that Sum of exterior angles / Sum of interior angles = 1/5 (ii)
By equating (i) and (ii) we get,
360o/(n – 2) × 180° = 1/5
(n – 2) × 180° = 360o × 5
(n – 2) × 180° = 1800o
(n – 2) = 1800o/180o
(n – 2) = 10
n = 10 + 2 = 12
Hence Numbers of sides of a polygon is 12.
Question 24. PQRSTU is a regular hexagon, determine each angle of ΔPQT.
Solution:
As we know that the sum of interior angles of a polygon = (n – 2) × 180°
The sum of interior angles of a hexagon = (6 – 2) × 180° = 4 × 180° = 720°
Sum of each angle of hexagon = 720o/6 = 120o
∠PUT = 120o Proved.
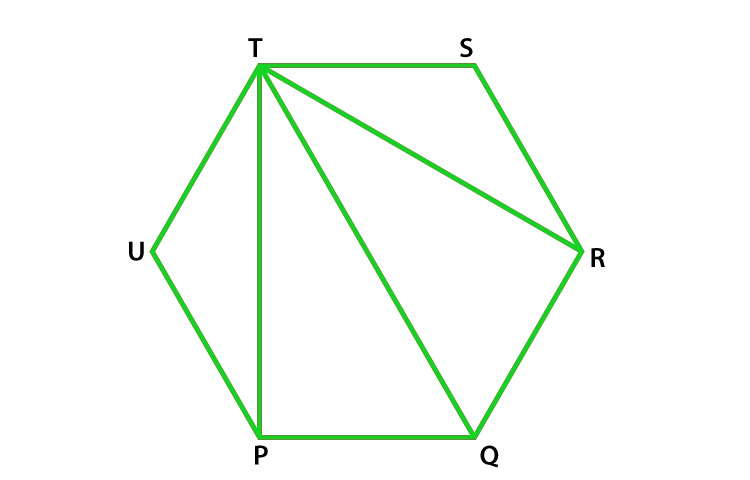
In Δ PUT
∠PUT + ∠UTP + ∠TPU = 180o (sum of triangles)
120o + 2∠UTP = 180o (Since Δ PUT is an isosceles triangle )
2∠UTP = 180o – 120o
2∠UTP = 60o
∠UTP = 60o/2 = 30o
∠UTP = ∠TPU = 30o similarly ∠RTS = 30o
therefore ∠PTR = ∠UTS – ∠UTP – ∠RTS
= 120o – 30o – 30o = 60o
∠TPQ = ∠UPQ – ∠UPT
= 120o – 30o = 90o
∠TQP = 180o – 150o = 30o (By using angle sum property of triangle in ΔPQT)
Hence ∠P = 90o, ∠Q = 60o, ∠T = 30o
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...