Divisibility Rules are the tests that were developed to make the division process simple and quicker. If we have to check whether a number is divisible by some other number, we can use these rules and check the same without the long division method.
Let’s learn what are divisibility tests in mathematics and their rules in detail.
Divisibility Rules in Math
Divisibility rules are some shortcuts to find if an integer is divisible by a number without actually doing the whole division process. These rules can help us determine the prime factorization relatively fast or in simplifying fractions.
For example, let’s suppose a boy has 531 chocolates, and he has to distribute them among his 9 friends. Dividing 531 by 9, we get no remainder, which means 531 is perfectly divisible by 9. If that boy knows divisibility rules he can easily tell whether or not he can divide the chocolates equally. Let’s check all important divisibility rules.
Here are divisibility rules of numbers from 1 to 19.
|
Table for the Divisibility Test
|
|
Divisibility by number
|
Divisibility rule
|
|
Divisibility by 2
|
The last digit should be even. |
|
Divisibility by 3
|
The sum of the digits should be divisible by 3. |
|
Divisibility by 4
|
The last two digits should be divisible by 4. |
|
Divisibility by 5
|
The last digit should either be 0 or 5. |
|
Divisibility by 6
|
The number should be divisible by both 2 and 3. |
|
Divisibility by 7
|
The double of the last digit, when subtracted by
the rest of the number, the difference obtained
should be divisible by 7. |
|
Divisibility by 8
|
The last three digits should be divisible by 8. |
|
Divisibility by 9
|
The sum of the digits should be divisible by 9. |
|
Divisibility by 10
|
The last digit should be 0. |
|
Divisibility by 11
|
The difference of the alternating sum of digits
should be divisible by 12. |
|
Divisibility by 12
|
The number should be divisible by both 3 and 4. |
|
Divisibility by 13
|
The four times of the last digit, when added to
the rest of the number, the result obtained
should be divisible by 13. |
|
Divisibility by 17
|
The five times of the last digit, when subtracted by
the rest of the number, the difference obtained
should be divisible by 17. |
|
Divisibility by 19
|
The double of the last digit, when added to
the rest of the number, the result obtained
should be divisible by 19. |
Divisibility Rule of 1
As all the numbers are divisible by 1 so it doesn’t need any test to determine that. Any number k can be written as k×1, thus we can divide k by 1 and still have k left. For example, if 2341 is divided by 1, we have 2341 as the quotient and 0 as the remainder.
Divisibility Rule of 2
A number is divisible by 2 if the last digit of the number is any of the following digits 0, 2, 4, 6, 8. The numbers with the last digits 0, 2, 4, 6, and 8 are called even numbers.
Example: 2580, 4564, 90032 etc. are divisible by 2.
Divisibility Rule of 3
A number is divisible by 3 if the sum of its digits is divisible by 3.
Example: 90453 (9 + 0 + 4 +5 + 3 = 21) 21 is divisible by 3. 21 = 3 × 7. Therefore, 90453 is also divisible by 3.
Divisibility Rule of 4
A number is divisible by 4 if the last two digits are divisible by 4.
Example: 456832960, here the last two digits are 60 that are divisible by 4 i.e.15 × 4 = 60. Therefore, the total number is divisible by 4.
Divisibility Rule of 5
A number is divisible by five if the last digit of that number is either 0 or 5.
Example: 500985, 3456780, 9005643210, 12345678905 etc.
Divisibility Rule of 6
A number is divisible by 6 if it is divisible by both 2 and 3.
Example: 10008, have 8 at one’s place so is divisible by 2 and the sum of 1, 0, 0, 0 and 8 gives the total 9 which is divisible by 3. Therefore, 10008 is divisible by 6.
Divisibility Rule of 7
Following are the steps to check the divisibility rule for 7,
- Take the last digit and then double the last digit.
- Subtract the result from the remaining number.
- If the number is 0 or a multiple of 7, then the original number is divisible by 7. Else, it is not divisible by 7.
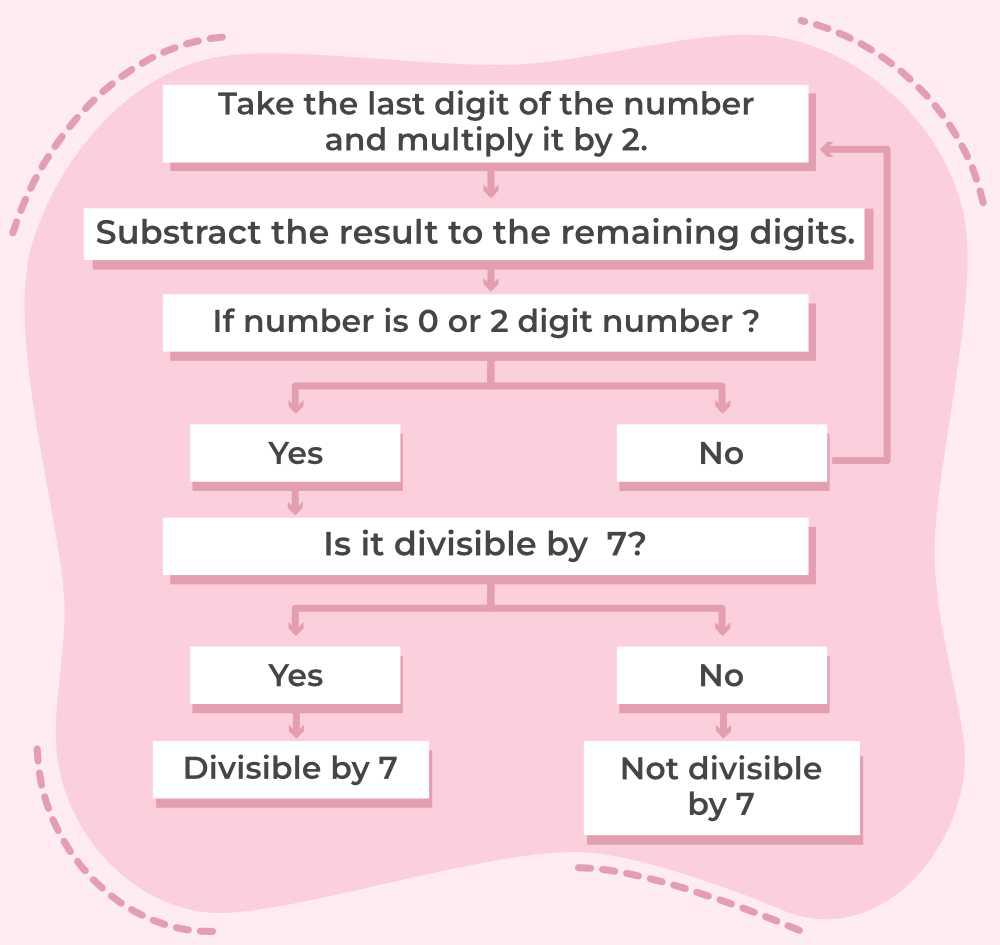
Example: Consider the number 5497555 to test if it is divisible by 7 or not. Add the last two digits to twice the remaining number and repeat the same process until it reduces to a two-digit number. If the result obtained is divisible by 7 the number is divisible by 7.
55 + 2(54975) = 109950 + 55 = 110005
05 + 2(1100) = 2200 + 05 = 2205
05 + 2(22) = 44 + 5 = 49
Reduced to the two-digit number 49, which is divisible by 7 i.e, 49 = 7 × 7
Divisibility Rule of 8
To check the divisibility rule for 11, if a number is divisible by 8 its last three digits should be divisible by 8.
Example: 008 which is divisible by 8, therefore, the total number is divisible by 8.
Divisibility Rule of 9
A number is divisible by 9 if the sum of its digits is divisible by 9. In example 90453, when we add the digits, we get the result as 21, which is not divisible by 9.
Example: 909, 5085, 8199, 9369 etc are divisible by 9. Consider 909 (9 + 0 + 9 = 18). 18 is divisible by 9(18 = 9 × 2). Therefore, 909 is also divisible by 9.
Note A number that is divisible by 9 also divisible by 3, but a number that is divisible by 3 does not have surety that it is divisible by 9.
Example: 18 is divisible by both 3 and 9 but 51 is divisible only by 3, can’t be divisible by 9.
Divisibility Rule of 10
A number is divisible by 10 if it has only 0 as its last digit. A number that is divisible by 10 is divisible by 5, but a number that is divisible by 5 may or may not be divisible by 10.10 is divisible by both 5 and 10, but 55 is divisible only by 5, not by 10.
Example: 89540, 3456780, 934260, etc are all divisible by 10.
Divisibility Test for the Number 10
Divisibility Tips and Tricks
Following table is the best way to understand the shortcut of the divisibility rules from 2 to 10,

Divisibility Test Tips and Tricks Chart
Divisibility Rule of 11
To check the divisibility rule for 11, if the difference of the sum of alternative digits of a number is divisible by 11, then that number is divisible by 11 completely.
Example: Let us consider a number to test the divisibility with 11, 264482240 mark the even place values and odd place values. Sum up the digits in even place values together and sum up the digits in odd place values together.
|
Digits
|
Place Value
|
|
2
|
0
|
|
6
|
1
|
|
4
|
2
|
|
4
|
3
|
|
8
|
4
|
|
2
|
5
|
|
2
|
6
|
|
4
|
7
|
|
0
|
8
|
Now sum up the digits in even place values i.e., 0th + 2th + 4th + 6th + 8th = 2 + 4 + 8 + 2 + 0 = 14. To add up the digits in odd place values i.e., 1th+ 3th + 5th + 7th = 6 + 4 + 2 + 4 = 14
Now calculate the difference between the sum of digits in even place values and the sum of digits in odd place values if the difference is divisible by 11 the complete number i.e., 264482240 is divisible by 11. Here the difference is 0, (14-14) which is divisible by 11. Therefore, 264482240 is divisible by 11.
Divisibility Rule of 12
For any number to be divisible by 12, it must be divisible by 3 as well as 4 simultaneously. So, the divisibility rule of 3 and 4 is used together to check whether a number is divisible by 12 or not.
For example, let’s check whether 3276 is divisible by 12 or not.
Divisibility by 3, 3 + 2 + 7 + 6 = 18, which is divisible by 3.
Thus 3276 is divisible by 3.
As 76 is the last two digits of 3276, and 76 is divisible by 4 (76 = 4×19).
Thus, 3276 is divisible by 4 as well.
As 3276 is divisible by 3 and 4 simultaneously, thus 3276 is divisible by 12 as well.
Note: For all the composite numbers such as 14, 16, 18, 20, etc., we can check their divisibility using the divisibility rule of their constituents factors.
Divisibility Rule For 13
To check, if a number is divisible by 13, add 4 times the last digit to the rest of the number and repeat this process until the number becomes two digits. If the result is divisible by 13, then the original number is divisible by 13.

Divisibility Test For the Number 13
Example: Check whether 333957 is divisible by 13 or not.
Solution:
Unit digit of 333957 is 7,
(4 × 7) + 33395 = 33423
(4 × 3) + 3342 = 3354
(4 × 4) + 335 = 351
(1 × 4) + 35 = 39
(1 × 4) + 35 = 39
Reduced to two-digit number 39 is divisible by 13.
Therefore, 33957 is divisible by 13.
Divisibility Rule of 17
A number is divisible by 17, when dividing it by 17 there is no remainder left. To check, if a number is divisible by 17, subtract 5 times the last digit from the rest of the number and repeat this process until the number becomes two digits.
If the result is divisible by 17, then the original number is also divisible by 17.

Divisibility Test for the number 17
Example: Is 28730 divisible by 17 or not?
Solution:
Unit digit of 28730 is 0,
2873 – (5 × 0) = 2873
287 – (5 × 3) = 272
27 – (5 × 2) = 17
Reduced to two-digit number 17 is divisible by 17.
Therefore, 28730 is divisible by 17.
Divisibility Rule of 19
To check, if a number is divisible by 19, take its unit digit and multiply it by 2, then add the result to the rest of the number, and repeat this step until the number is reduced to two digits.
If the result is divisible by 19, then the original number is also divisible by 19. Otherwise, the original number is not divisible by 19.
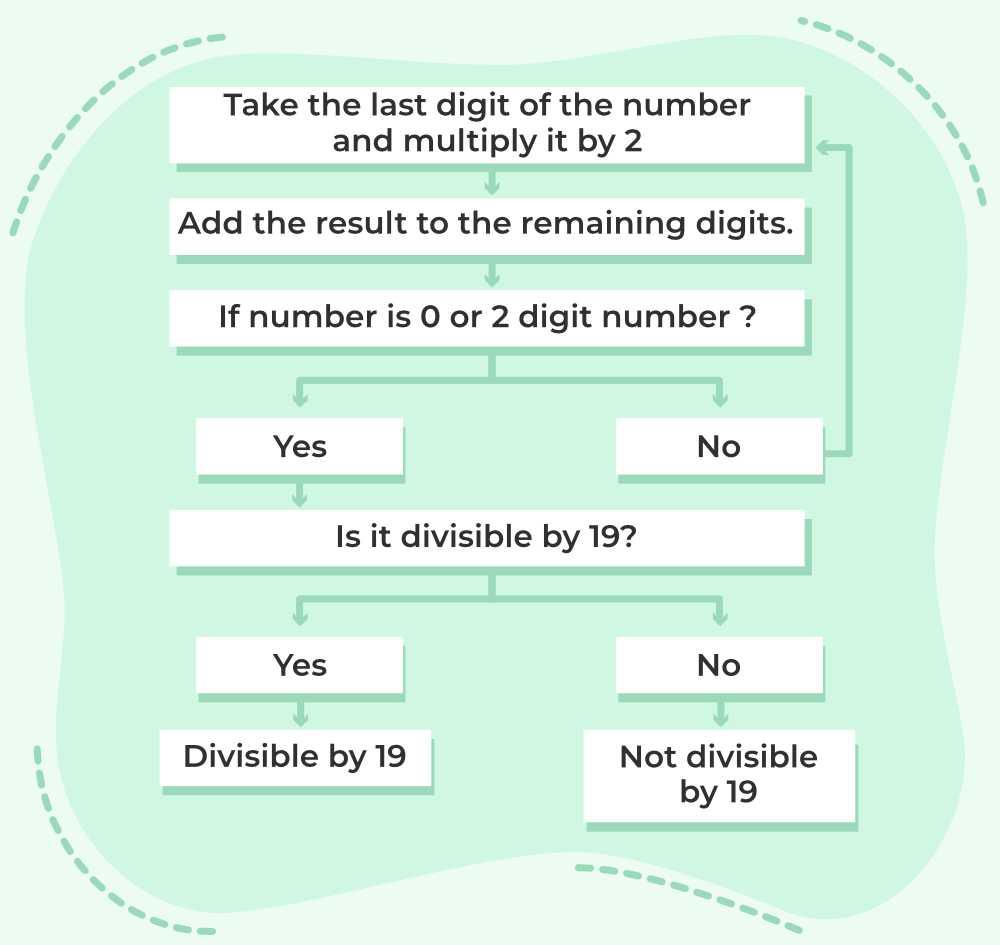
Divisibility Test for the number 19
Example: Is 12635 divisible by 19 or not?
Solution:
Unit digit of 12635 is 5,
1263 + (2× 5) = 1273
127 + (2 × 3) = 133
13 + (2 × 3) = 19
Reduced to two-digit number 19 is divisible by 19.
Therefore, 12635 is divisible by 19.

Also, Read:
Divisibility Rules Examples
Example 1: Determine the number divisible by 718531.
Solution:
Since, the given number contains 1 in the one’s-place, therefore it is clear that it must be divisible either by 3, 7, 9 or 11.
First add all the digits of the given number, 7 + 1 + 8 + 5 + 3 + 1 = 25 which is not divisible by 3 or 9, so 718531 is also not divisible by 3 or 9.
Lets sum up all the even places digits, 3 + 8 + 7 = 18
and now sum up all odd places digits, 1 + 5 + 1 = 7
Now subtract them as:
18 – 7 = 11
Therefore, the given number 718531 is divisible by 11.
Example 2: Use divisibility rules to check whether 572 is divisible by 4 and 8.
Solution:
Divisibility rule for 4 – The last two digits of 572 is 72 (i.e. 4 x 18) is divisible by 4.
Therefore, the given number 572 is divisible by 4.
Divisibility rule for 8 – The last three digits of 572 is,
572 = 2 × 2 × 11 × 13
This implies that, the given number does not contain 8 as its factor, so 572 is not divisible by 8.
Example 3: Check whether the number 21084 is divisible by 8 or not. If not, then find what that number is?
Solution:
The last three digits of the given number 21084 is,
084 or 84 = 2 × 2 × 3 × 7
This implies that, the given number does not contain 8 as its factor, so 21084 is not divisible by 8.
Since, the one’s place digit of 21084 is 4 therefore it is clear that 21084 is divisible by 2.
Now, to check the divisibility rule for 4, consider its last two-digits: 84 i.e. 4 × 21.
This implies that, 21084 is divisible by 4.
Hence, 21084 is divisible by 2 and 4.
FAQs on Divisibility Rules
What are Divisibility Rules?
Divisibility rules are the trick to finding out whether a number is divisible by another number without doing the actual calculation.
What are the Divisibility Rule of 3 and 9?
A number is divisible by 3 if the sum of its digits is divisible by 3. Similarly, A number is divisible by 9 if the sum of its digits is divisible by 9. For example, 39 is divisible by 3, as 3 + 9 = 12, which is divisible by 3. Therefore, 39 is divisible by 3. 2397 is divisible by 9, as 2 + 3 + 9 + 7 = 21, which is divisible by 9.
What is the Divisibility Rule of 13?
The divisibility rule for 13 is to add four times the last digit of the number to the remaining number until a two-digit number is obtained. If the two-digit number is divisible by 13, the number too is divisible by 13.
For example, Take 1001
Adding 4 to 100, 100 + 4 = 104
Adding 16 to 10, 10 + 16 = 26
Now since 26 is divisible by 13, 1000 is divisible by 13.
What is the Divisibility Rule of 7?
The divisibility rule for 7 is to subtract 4 times the unit digit from the rest of the number, until the result is either 0 or a two-digit number. If the result is 0 or a two-digit number that is divisible by 7, then the original is also divisible by 7. Otherwise, the original number is not divisible by 7.
What is the DIvisibility Rule of 11?
To check if the given number is divisible by 11 or not, we find the difference between the alternating digits of the number. If the difference is divisible by 11 or 0, then the original number is also divisible by 11. Otherwise, the original number is not divisible by 11.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...