Faces, Edges and Vertices are the three basic properties that are used to define various 3D objects. They have different dimensions like length, width, and height.
In this article, we are going to learn about the vertices, faces, and edges of different 3D shapes in detail.
What are Faces
A face is defined as the flat surface of a solid. It can be referred to as the outer surface of a solid object, whether it be a curved face or a straight face.
The figure given below is a cuboid that has six faces, i.e., ABCD, EFGH, ADHE, AEFB, BFGC, and DHGC.

What are Edges
An edge is defined as the line segment where the faces of a solid meet. Even though many shapes have straight edges and lines, some shapes, like hemispheres, have curved edges.

What are Vertices
In geometry, a vertex is a point of intersection of two or more curves, lines, or edges. They are represented as points and denoted by letters such as A, B, C, D, etc.
The figure given below is a cuboid that has eight vertices, i.e., A, B, C, D, E, F, G, and H.

Types of Polyhedron
Polyhedron is referred to as a three-dimensional solid that is made up of polygons. It consists of flat polygonal faces, straight edges, and sharp corners called vertices.
Some examples of polyhedrons are cubes, pyramids, prisms, etc. Different types of polyhedrons have been discussed in the table below :
| Types of Polyhedron |
Description |
Examples |
| Regular Polyhedron |
A polyhedron whose faces are regular, congruent polygons. |
Tetrahedron, Cube, Regular Octahedron, Regular Dodecahedron, Regular Icosahedron |
| Irregular Polyhedron |
A polyhedron made up of irregular polygonal faces that are not congruent to each other. |
Pentagonal Pyramid, Triangular Prism, Octagonal Prism |
| Convex Polyhedron |
A polyhedron where the line segment joining any two points lies within its interior or surface, and the surface does not intersect itself. |
Cube, Regular Tetrahedron, Prism |
| Concave Polyhedron |
A non-convex polyhedron where at least one line segment joining two points of the polyhedron lies outside its surface. |
Star-shaped Polyhedrons, Concave Cubes |
Note : As cones, cylinders, and spheres do not have polygonal faces and curved surfaces, they are non-polyhedrons.
Vertices, Faces and Edges of 3D Shapes
Now we will find the vertices, faces and edges of various solid shapes with the help of a table given below.
|
Shape
|
Figure |
Vertices
|
Edges
|
Faces
|
|
Cube
|
 |
8
|
12
|
6
|
|
Cuboid
|
 |
8
|
12
|
6
|
|
Cone
|
 |
1
|
1
|
2
|
|
Cylinder
|
 |
0
|
0
|
3
|
|
Sphere
|
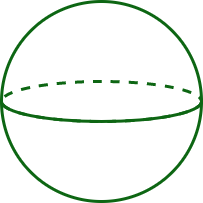 |
0
|
0
|
1
|
|
Triangular Prism
|
 |
6
|
9
|
5
|
|
Rectangular Prism
|
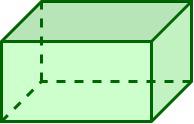 |
8
|
12
|
6
|
|
Square Prism
|
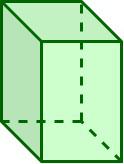 |
8
|
12
|
6
|
|
Pentagonal Prism
|
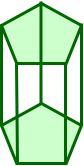 |
10
|
15
|
7
|
|
Hexagonal Prism
|
 |
12
|
18
|
8
|
|
Triangular Pyramid
|
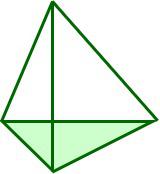 |
4
|
6
|
4
|
|
Rectangular Pyramid
|
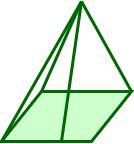 |
5
|
8
|
5
|
|
Square Pyramid
|
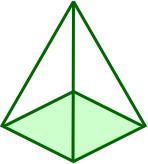 |
5
|
8
|
5
|
|
Pentagonal Pyramid
|
 |
6
|
10
|
6
|
|
Hexagonal Pyramid
|
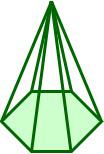 |
7
|
12
|
7
|
Euler’s Formula
The relationship between vertices, faces, and edges can be determined using Euler’s formula. Euler’s formula states that for any convex polyhedron, the sum of the number of faces (F) and vertices (V) is exactly two greater than the number of edges (E).
Relation Between Faces, Edges And Vertices :
F + V = 2 + E
where,
F is the number of faces,
V is the number of vertices,
E is the number of edges
Euler’s formula is applicable for closed solids that have flat sides and straight edges, such as cuboids. It is not applied to solids that have curved edges, such as cylinders, spheres, etc.
Related :
Faces, Edges And Vertices Examples
Example 1: Verify Euler’s formula for the heptahedron.
Solution:
A heptahedron has 7 faces, 10 vertices, and 15 edges.
From Euler’s formula, we have,
F + V = 2 + E
⇒ 7 + 10 = 2 + 15
⇒ 17 = 17
Hence, Euler’s formula is verified for the heptahedron.
Example 2: Calculate the number of edges of a polyhedron if it has 6 vertices and 9 faces.
Solution:
Given data,
V = 6 and F = 5
From Euler’s formula, we have,
F + V = 2 + E
⇒ 5 + 6 = 2 + E
⇒ 11 = 2 + E
⇒ E = 11 – 2 = 9
Hence, the given polyhedron has 9 edges.
Example 3: Calculate the number of vertices of a polyhedron if it has 5 faces and 8 edges.
Solution:
Given data,
F = 5 and E = 8
From Euler’s formula, we have,
F + V = 2 + E
⇒ 5 + V = 2 + 8
⇒ 5 + V = 10
⇒ V = 10 – 5 = 5
Hence, the given polyhedron has 5 vertices.
FAQs on Faces, Edges And Vertices
What is polyhedron?
In geometry, a polyhedron is referred to as a three-dimensional solid that is made up of polygons. A polyhedron consists of flat polygonal faces, straight edges, and sharp corners called vertices. Some examples of polyhedrons are cubes, pyramids, prisms, etc.
What are Vertices, Faces and Edges?
A vertex (plural: vertices) is a point where two or more lines meet. An edge is the line segment that connects two vertices, forming the skeleton or outline of a shape. A face is a flat surface enclosed by edges. In a three-dimensional object, such as a cube, the vertices are the corners, the edges are the lines connecting these corners, and the faces are the flat surfaces bounded by these edges.
How Many Vertices, Faces and Edges does a Cone have?
A cone has 1 vertex, 2 faces, and 1 edge.
How Many Vertices, Faces and Edges does a Cylinder have?
A cylinder has 0 vertices, 3 faces, and 2 edges.
How Many Vertices, Faces and Edges does a Cube have?
A cube has 8 vertices, 6 faces, and 12 edges.
How Many Vertices, Faces and Edges does a Cuboid have?
A cuboid has 8 vertices, 6 faces, and 12 edges.
What is a face of a solid?
A face is defined as the flat surface of a solid. It can be referred to as the outer surface of a solid object, whether it be a curved face or a straight face. For example, a cube has six faces, a tetrahedron has four faces, a cylinder has three faces, i.e., a curved face and two circular faces, a cone has two faces, i.e., a curved face and a flat face, whereas a sphere has a curved surface.
State Euler’s Formula.
The relationship between vertices, faces, and edges can be determined using Euler’s formula. Euler’s formula states that for any convex polyhedron, the sum of the number of faces (F) and vertices (V) is exactly two greater than the number of edges (E).
Euler’s Formula:
F + V = 2 + E
where,
F is the number of faces,
V is the number of vertices,
E is the number of edges
Share your thoughts in the comments
Please Login to comment...