Mensuration – Volume of Cube, Cuboid, and Cylinder | Class 8 Maths
Last Updated :
08 Apr, 2024
Mensuration is the branch of mathematics which deals with the study of different geometrical shapes, their areas, and volume. It uses geometric calculations and algebraic equations to compute the measurement of various aspects of objects like Surface Area, Volume, etc.
Volume is the measurement of the amount of space inside a 3D object that can be filled. It can be the measurement of any solid object like cube, square, cylinder, sphere, pyramid, etc. Volume of an object is usually measured using cubic units. By finding out the volume of an object it also helps us find the amount required to fill an object
The S.I. unit of volume is m3. Other units are ml or L.
Note: 1m3 = 1000 Litre
How to Find Volumes of 3D Objects
Till now you must have understood the meaning of volume, let’s move to find the volume of various 3D geometrical figures like cubes, cuboids, and cylinders.
Finding Volume of a Cuboid
A cuboid is a three-dimensional structure having six rectangular faces. The volume of a cuboid is equal to the product of length, breadth, and height of the cuboid. In rectangular cuboid, all the angles are at right angles and the opposite faces of a cuboid are equal.
Let l is the length, b is the breadth and h is the height of the cuboid.

Let’s consider some example related to the calculation of volume of cuboid.
Example 1: Calculate the volume of the cuboid where length, breadth, and height are 12, 8, and 4 meters respectively.
Solution:
Given, Length=12m
Breadth = 8m
Height = 4m
Applying the Formula,
Volume of cuboid = length × breadth × height
⇒ Volume of cuboid = 12 × 8 × 4 = 384 m3
Thus, volume of the given cuboid is 383 m3.
Example 2: Calculate the breadth of the cuboid whose volume is given as 350-meter cube. And length and height are 7 and 5 meters respectively.
Solution:
Given Volume of cuboid = length × breadth × height
350 = 7 × breadth × 5
⇒ 350/35 = breadth
⇒ 10m = breadth
Thus, breadth of the given cuboid is 10 m.
Volume of a Cube
Firstly the question arises what is cube? So, Cube is a three-dimensional shape with equal width, height, and length measurements. Basically, a cuboid whose length, width, and height are equal is called a cube.
Since we know the volume of cuboid = length × breadth × height and the cube is a special case of cuboid where all length, breadth, and height are equal. Let’s assume length = breadth = height = a
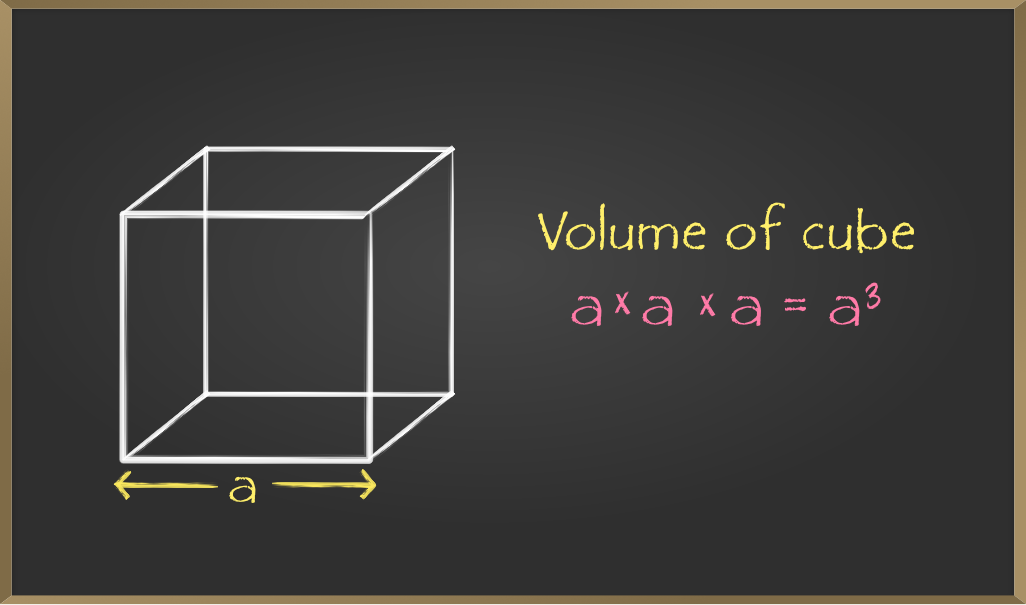
Let’s consider some example related to the calculation of volume of cube.
Example 1: Find the volume of a cube with sides of length 10 cm.
Solution:
We know, V = (a3)
⇒ V = (103) cm3
So, Volume of the given cube is 300 centimeter cube
Example 2: Find the length of the sides of the cube whose volume is 343centimeter cube
Solution :
As we know, Volume of cube = side3
343= (side)3
⇒ 7 cm = side
Thus, side of the cube with volume 343 is 7 cm.
Volume of Cylinder
A cylinder is a three-dimensional solid that contains two parallel bases connected by a curved surface. The bases are usually circular in shape. The perpendicular distance between the bases is denoted as the height “h” of the cylinder and “r” is the radius of the cylinder.

Let’s consider some example related to the calculation of volume of cylinder.
Example 1: Calculate the volume of the cylindrical container having a radius of 4 cm and height of 35 cm.
(Take pi = 22/7)
Solution:
Radius = 4cm
Height = 35cm
Putting the values in the formulae,
Volume of cylinder = π × 4 × 4 × 35
⇒ Volume of cylinder = π × 560 (pi = 22/7)
⇒ Volume of cylinder = 1760 cm3
Example 2: Calculate the radius of the cylinder whose height is 21 cm and volume of the cylinder is 1100 centimeter cube?(Take pi = 22/7)
Solution:
Volume of cylinder = πr2h cubic units
⇒ 1100 = 22/7 × r2 × 21
⇒ r2 = (1100 x7) ÷ (22 x21)
⇒ r2 = 7700 ÷ 462
⇒ r2 = 16.66
⇒ r = √16.66
⇒ r = 4.0825
radius of the cylinder is approximately = 4.0825 cm.
Share your thoughts in the comments
Please Login to comment...