Percentage– Percentage in mathematics is a number or ratio that represents a fractional part of a per cent, i.e., per 100. The word “Percentage” was coined from the Latin word “Percentum” which means “by hundred“. It is a dimensionless relation between two numbers. It is often denoted by the sign “%” or per cent or pct.
Examples of percentages are:
- 10% is 10/100, that is, 1/10 of the number
- 20% is 20/100, that is, 1/5 of the number
In this article, will learn about Percentages, Percentage Formulas, How to Calculate Percentages, and others in detail.
What is Percentage?
A fraction whose denominator is 100 is called a Percent i.e. in all the fractions where the denominator is 100 we can remove the denominator and put the % sign.
For example, the fraction 23/100 can be written as 23%. The opposite of this is also true i.e. any percentage sign can be easily replaced by converting the number into a fraction with the denominator 100. For example, 45% can be converted to a fraction as 45/100.
- Percentages are also called dimensionless numbers, as they have no dimension. They are the ratio of two numbers with the same dimensions. If we say 10% of a number that means 10 per cent of its whole.
- Percentages can also be represented in decimal Values like 0.5%, 0.75%, etc.
Check: Percentages – Aptitude Questions and Answers
Examples of Percentage
Some examples of fractions include,
- If Kabir scores 95 marks out of 100 in the mathematics examination then it is changed in fraction as, 95/100 = 95%
- If candidate A scores 2450 votes out of 10000 votes then it is represented in percentage as, 2450/1000 = 24.5/100 = 24.5%
Similarly,
- 10/100 in percentage = 10%
- 50/100 in percentage = 50%
- 100/100 in percentage = 100%
The image given below shows us some examples where the percentage is used.
.jpg)
Percentage formula is a formula that is used to find the amount or share of a quantity in terms of a hundred. So, for calculating the percentage, we basically need three variables. First, the total value V1, the present value V2, and the percentage value P. The algebraic equation for this will be:
Percentage (P%) = (Parts (V2) / Whole (V1)) × 100

How to Calculate Percentage of a Number?
Calculating percentage of a number is very simple, you just need to use the formula mentioned below:
Percent of a Number = Percentage/100 × Number
Example:
Calculate 5% of 50
5% of 50 = 5/100 × 50
5% of 50 = 0.05 × 50
5% of 50 = 2.50
Percentage difference or the percentage change formula is calculated when the difference between two values is divided by the average of the same values. We can say that the percentage difference is used to calculate the change in the value over the given period. Mathematically, we can be written as,
Check: Basic Concept of Percentage
Percentage Difference = (Absolute difference / Average) × 100
Example: Percentage difference between 50 and 100 will be:
= |50-100|/ {(50+100)/2} × 100
= 50/75 ×100
= 66.66%
It is expressed as a ratio and is a unitless number
We can use the percentage difference formula to find the change in the value when it increases over a time period. The percentage increase formula is given below,
Percentage Increase = (Increase value – Original value / Average) × 100
We can use the percentage difference formula to find the change in the value when it decreases over a time period. The percentage decrease formula is given below,
Percentage Decrease = (Original value – Decrease value / Average) × 100
Note:
- If the value obtained is negative while calculating percentage increase formula, then it is actually percentage decrease.
- If the value obtained is negative while calculating percentage decrease formula, then it is actually percentage increase.
- Percentage change is also used to find the percentage errors in maths, physics and chemistry.
How To Calculate Percentage?
The most important question is how to calculate percentage. So, percentages can easily be calculated when the values are given as fractions with a denominator of 100. If not, we have to convert the given fraction into a fraction with a denominator of 100, and then the percentage is easily calculated.
Check: How to Calculate Percentage?
For example, if 65/100 is to be calculated as a percentage then the answer can easily be calculated by removing the denominator 100 and applying the % symbol i.e 65%.
Example: Convert 0.76 into the percentage.
Solution:
0.76 = 0.76/1
0.76 = 76/100
0.76 = 76 %
How To Calculate Percentage when Total is 100?
If the total value in any scenario adds up to 100 then calculating the percentage is very easy as the number (in the numerator of the value) itself represent the percentage and the % symbol is added.
Example: Suppose in the election of a class representative if student A got 69 votes and student B got 31 votes then find the percentage of votes A got.
Solution:
Total votes = 69 + 31 = 100
A got votes = 69
Votes of A (in percentage) = 69/100 = 69%
How To Calculate Percentage when Total is NOT 100?
If the total value in any scenario does not add up to 100 then the percentage is calculated by making the total 100 in the fraction and then the numerator values become the percentage.
Example: Suppose Kabir got 6 blue balls, 8 red balls, and 6 yellow balls the percentage of red balls he has?
Solution:
Total balls = red balls + blue balls + yellow balls
= 8 + 6 + 6 = 20 balls
Red balls = 8 balls
Percentage of red balls = 8/20
= (8/20) × (5/5) = 40/100 = 40%
Converting Percentage to Fraction
In some cases, we are provided with the percentage and need to convert it to a fraction number. For converting percentages to fractions, some calculations are required. We can use the formula,
Check: Problems on Percentage
Fraction = Percentage/100
After getting it to reduce it further. For example,
- Fraction of 25% = 25/100 = 1/4
- Fraction of 50% = 50/100 = 1/2
- Fraction of 75% = 75/100 = 3/4
- Fraction of 90% = 90/100 = 9/10
Converting Fraction to Percentage
For converting fraction to a percentage, let’s assume the fraction is represented by a/b, where “a” is part of the whole “b”. Multiplying numerator and denominator by 100.
[Tex]\frac{a}{b} \times \frac{100}{100}= (\frac{a}{b} \times 100) \times \frac{1}{100}
[/Tex]
We know that 1/100 = 1%
Therefore, the equation can be written as,
a/b × 100%.
Hence, to convert a fraction to a percentage, multiply the fraction by 100.
Percentage Chart
Let’s see the percentage chart of fractions converted into percentages,
Percentage Chart
|
|---|
| Fraction | Percentage | Fraction | Percentage |
|---|
1/1
| 100%
| 1/11
| 9.09%
|
1/2
| 50%
| 1/12
| 8.33%
|
1/3
| 33.33%
| 1/13
| 7.69%
|
1/4
| 25%
| 1/14
| 7.14%
|
1/5
| 20%
| 1/15
| 6.66%
|
1/6
| 16.66%
| 1/16
| 6.25%
|
1/7
| 14.28%
| 1/17
| 5.88%
|
1/8
| 12.5%
| 1/18
| 5.55%
|
1/9
| 11.11%
| 1/19
| 5.26%
|
1/10
| 10%
| 1/20
| 5%
|
Percent Table
The image added below shows the percentage table,

Difference between Percentage and Percent
The words percentage and percent are related to each other, but there is a difference between both them. Percent is always accompanied by a number, for example, 25%.
While percentage does not need a number to be accompanied by the term.
For example, the percentage of people who participated in the voting in 2022 is more than the percentage of people who participated in 2021.
Fractions, decimals, ratios and percentages are also related to each other.
Percentage in Maths
In mathematics, the percentage is written with three possible unknowns and variables. The three terms are known:
For instance, 50% of 400 is 200. Here, 50 is the percentage, 400 is the base, and 200 is part.
Example: If 25% of 200 is 50, explain the different terms in the calculation.
25% of 400 is 50. Here 25 is the percentage, 200 is the base, and 50 is the part.
In fraction, it can be written as,
Part/Base = 25/200 = 1/4
1/4 is the fraction obtained. However, we have learned how to convert fractions into percentages. Therefore, multiply 1/4 by 100,
1/4 × 100 = 25%.
Percentage Tricks
There are percentage tricks that can be used while calculating the percentage of numbers. Below given trick is the most used,
% x of y = % y of x
Example: Solve 300% of 50.
Here, solving 300% of 50 can be a little lengthy and tricky. However, using the trick it can be easily solved,
%x of y = %y of x
300% of 50 = 50% of 300
Now, solving 50% of 300 is relatively is. 50% of 300 is just half of 300. Therefore, 50% of 300 is 150.
Therefore, 300% of 50 is 150.
How to Calculate percentage of marks
The percentage is mostly used when marks are calculated for students. The marks of students are with respect to the total marks. That fraction is converted into a percentage by multiplying it by 100. In this way, we can calculate the marks in percentage. Let’s see some examples of marks obtained in percentage,
| Marks obtained | Total marks | Marks in Percentage (%) |
|---|
| 50 | 100 | 50/100 × 100 = 50% |
| 25 | 50 | 25/50 × 100 = 50% |
| 80 | 100 | 80/100 × 100 = 80% |
| 33 | 100 | 33/100 × 100 = 33% |
Percentage Calculator
Percentage calculator is a free tool prepared at GeeksforGeeks that is used to find the percentage if two or more numbers are given. The percentage calculator for the same is added on our website.
Read More,
Solved Example of percentage
Some examples on the percentages are,
Example 1: Find 15 % of 500.
Solution:
We can find the percentage by formula,
V2 = P × V1
V2 = 15% × 500
V2 = (15 × 500) / 100
V2 = 75.
Thus, 15% of 500 is 75.
Check: Percentage Questions
Example 2: Find 4% of 1300.
Solution:
We can find the percentage by formula,
V2 = P × V1
V2 = 4% × 1300
V2 = (4 × 1300) / 100
V2 = 52.
Thus, 4% of 1300 is 52.
Example 3: What percentage is 1 of 3000?
Solution:
We can find the percentage by formula,
V2 = P × V1
P = V2 / V1
P = 1 / 3000
Thus, P% = 1/3000 × 100
P% = (1/30)%
Thus, (1/30)% of 2000 is 500.
Example 4: If 10% of x is 900. Find x.
Solution:
We can find the percentage by the formula,
V2 = P × V1
V1 = V2 / P
V1 = (V2 × 100 ) / P%
V1 = (900 × 100) / 10
V1 = 9000
Thus, the value of x is 9000.
Example 5: Find the value of the percentage of green blocks in each case.
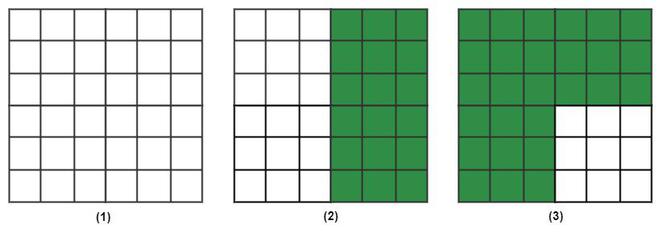
Solution:
In first case, the green blocks are 0, and the total blocks are 36.
Therefore,
Percentage of green Blocks = 0/36 × 100 = 0%.
In second case, the green blocks are 18, and the total blocks are 36.
Therefore,
Percentage of green Blocks = 18/36 × 100 = 50%.
In third case, the green blocks are 27 and the total bricks are 36.
Therefore,
Percentage of green Blocks = 27/36 × 100 = 75%.
Example 6: What percentage is 15 out of 50?
Original value = 15
Total value = 50
Percentage Formula is,
Percentage = (Original Value/Total value) × 100
= 15/ 50 × 100
= 30%
Example 7: What percentage of 80 is 20?
Original value = 20
Total value = 80
Percentage Formula is,
Percentage = (Original Value/Total value) × 100
= 20/ 80 × 100
= 25%
Practice Questions on Percentage
Q1: A boy obtained 450 Marks out of 500 in total. Find the Percentage of Marks.
Q2: Find the percentage of pure Gold Particles in 18 Carat of Gold given that 24 Carat is pure gold.
Q3: A 5 litre Acid bottle has concentration of 10%. Find the concentration of pure acid in the solution.
Q4: Ram obtained 223 marks out of 600 and failed the exam by 17 marks. Find the Passing Percentage of Marks.
Conclusion of Percentage
Percentages are like a universal language for proportions. Instead of wrestling with fractions or decimals, we can use percentages to express any part of a whole out of 100. This makes comparing things a breeze, whether it’s understanding discounts on a sale, visualizing survey results, or following a recipe. From everyday tasks to complex data analysis, percentages are a powerful tool for making sense of our world, one part at a time.
Percentage-FAQs
What is a percentage of 100%?
A percentage of 100% is actually 100 itself
How do you define percentage?
A percentage is a way of expressing a part of something compared to the whole, written as a fraction of 100.
What percent of 1 year is 1 day?
To calculate the percentage of 1 year that 1 day represents, we can divide the number of days in 1 day by the number of days in 1 year and then multiply by 100% (to express it as a percentage).
What is CGPA percentage?
The CGPA to percentage conversion is as simple as multiplying your CGPA by 9.5.
What is Percentage?
Percentage is the representation of numbers the literal meaning of the word percentage is out of 100. In percentage, the value is represented out of 100.
What is the symbol of Percentage?
The symbol of percentage is %. It is also known as per cent.
How to Calculate Percentage?
To calculate the percentage of a number, just divide the number obtained by the total numbers and multiply the fraction by 100
What is Percentage Change?
Percentage change of a number is the change in percentage from the old value to the new value. It is calculated using the formula,
Percentage Change = {(Difference between old value and new value) / Old value} × 100.
What are Examples of Percentages?
Percentage is very often used in our everyday lives, here are some examples of the real life usage of percentage.
- Percentage of different types of nutrients present is shown at the back of the food packets.
- Battery shows its power in percentage in our phones.
- Percentage of marks obtained by students in exam.
Can the percentage exceed 100?
Yes, the value of percentage can be more than 100, if the value given is more than the original value. For example, 40/20 is 200%.
Share your thoughts in the comments
Please Login to comment...