Theorem – There is one and only one circle passing through three given non-collinear points | Class 9 Maths
Last Updated :
06 May, 2021
Theorem Statement: There is one and only one circle passing through three given non-collinear points.
Required Diagram:

Given: Three non-collinear points P, Q, and R.
To Prove: There is one and only one circle passing through P, Q, and R.
Construction: Join PQ and QR. Draw perpendicular bisectors AL and BM of PQ and RQ respectively. Since P, Q, R is not collinear. Therefore, the perpendicular bisectors AL and BM are not parallel. Let AL and BM intersect at O. Join OP, OQ, and OR.
Proof
Since O lies on the perpendicular bisector of PQ. Therefore,
OP = OQ
Again, O lies on the perpendicular bisector of QR. Therefore,
OQ = OR
Thus, OP = OQ = OR = r (say).
Taking O as the centre draw a circle of radius s. Clearly, C (0, s) passes through P, Q, and R. This proves that there is a circle passing through the points P, Q, and R. We shall now prove that this is the only circle passing through P. Q and R. If possible, let there be another circle with centre O’ and radius r, passing through the points P, Q and R. Then, O’ will lie on the perpendicular bisectors AL of PQ and BM of QR. Since two lines cannot intersect at more than one point, so O’ must coincide with O. Since OP = r, O’P = s and O and O’ coincide, which means that,
r = s
Therefore,
C(O, r) ≅ (O’, s)
Hence, there is one and only one circle passing through three non-collinear points P, Q and R.
Examples
Example 1: Write down the step-by-step construction procedures to find out the centre of the circle?
Solution:
Let the circle be C1. We need to find its centre.
Step 1: Take points P, Q, R on the circle
Step 2: Join PR and RQ.
We know that the perpendicular bisector of a chord passes through the centre. So, we construct perpendicular bisectors of PR and RQ.
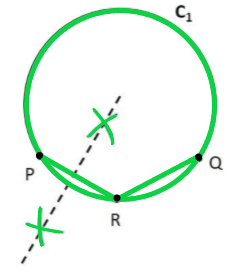
Step 3: Take a compass. With point P as the pointy end and R as the pencil end of the compass, mark an arc above and below PR. Do the same with R as pointy end P as pencil end of the compass.
Step 4: Join points intersected by the arcs. The line formed is the perpendicular bisector of PR.
Step 5: Take a compass, with point R as the pointy end and Q as pencil end of the compass mark an arc above and below RQ. Do the same with Q as the pointy end and R as the pencil end of the compass.
Step 6: Join the points intersected by the arcs. The line formed is the perpendicular bisector of RQ.
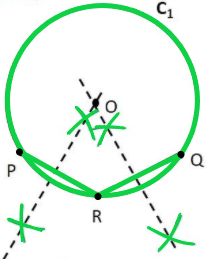
Step 7: The point where two perpendicular bisectors intersect is the centre of the circle. Mark it as point O. Thus, O is the centre of the given circle.
Example 2: Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
Solution:
(i) No point common:


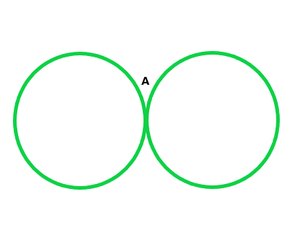
(ii) One point common:

(iii) Two points common:
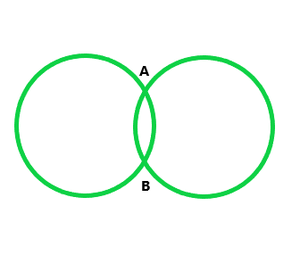
As we can analyze from above, two circles can cut each other maximum at two points.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...