Number of smaller circles that can be inscribed in a larger circle
Last Updated :
22 Apr, 2021
Given two positive integers R1 and R2, where R1 and R2 represent the radius of the larger and smaller circles respectively, the task is to find out the number of smaller circles that can be placed inside the larger circle such that the smaller circle touches the boundary of the larger circle.
Examples:
Input: R1 = 3, R2 = 1
Output: 6
Explanation: The radii of the circles are 3 and 1. Therefore, the circle of radius 1 can be inscribed in the circle of radius 3.

From the above representation, the total number of smaller circles that can be inscribed with touching of the boundary of the larger circle is 6.
Input: R1 = 5, R2 = 4
Output: 1
Approach: The given problem can be solved by finding the angle that the smaller circle of radius R2 makes at the centre of the circle with radius R1 and then divide it by 360 degrees.
Follow the steps below to solve the given problem:
- If the value of R1 is less than R2, then it is impossible to inscribe a single circle. Therefore, print 0.
- If the value of R1 is less than 2 * R2, i.e. if the diameter of the smaller circle is greater than the radius of the larger circle, then only one circle can be inscribed. Therefore, print 1.
- Otherwise, find the angle made by the smaller circle at the centreof the larger circle using the below formula and then, divide by 360 degrees to get the total number of circles that can be inscribed and print that value.
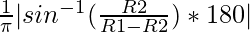
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int countInscribed(int R1, int R2)
{
if (R2 > R1)
return 0;
double angle;
double ratio;
int number_of_circles = 0;
ratio = R2 / (double)(R1 - R2);
if (R1 < 2 * R2) {
number_of_circles = 1;
}
else {
angle = abs(asin(ratio) * 180)
/ 3.14159265;
number_of_circles = 360
/ (2
* floor(angle));
}
return number_of_circles;
}
int main()
{
int R1 = 3;
int R2 = 1;
cout << countInscribed(R1, R2);
return 0;
}
|
Java
import java.util.*;
class GFG{
static int countInscribed(int R1, int R2)
{
if (R2 > R1)
return 0;
double angle;
double ratio;
int number_of_circles = 0;
ratio = R2 / (double)(R1 - R2);
if (R1 < 2 * R2)
{
number_of_circles = 1;
}
else
{
angle = Math.abs(Math.asin(ratio) * 180) /
3.14159265;
number_of_circles = (int)(360 /
(2 * Math.floor(angle)));
}
return number_of_circles;
}
public static void main(String args[])
{
int R1 = 3;
int R2 = 1;
System.out.println(countInscribed(R1, R2));
}
}
|
Python3
import math
def countInscribed(R1, R2):
if (R2 > R1):
return 0
angle = 0
ratio = 0
number_of_circles = 0
ratio = R2 / (R1 - R2)
if (R1 < 2 * R2):
number_of_circles = 1
else:
angle = (abs(math.asin(ratio) * 180) /
3.14159265)
number_of_circles = (360 / (2 *
math.floor(angle)))
return number_of_circles
if __name__ == "__main__":
R1 = 3
R2 = 1
print (int(countInscribed(R1, R2)))
|
C#
using System;
class GFG{
static int countInscribed(int R1, int R2)
{
if (R2 > R1)
return 0;
double angle;
double ratio;
int number_of_circles = 0;
ratio = R2 / (double)(R1 - R2);
if (R1 < 2 * R2)
{
number_of_circles = 1;
}
else
{
angle = Math.Abs(Math.Asin(ratio) * 180) /
3.14159265;
number_of_circles = (int)(360 /
(2 * Math.Floor(angle)));
}
return number_of_circles;
}
public static void Main()
{
int R1 = 3;
int R2 = 1;
Console.WriteLine(countInscribed(R1, R2));
}
}
|
Javascript
<script>
function countInscribed(R1, R2)
{
if (R2 > R1)
return 0;
let angle;
let ratio;
let number_of_circles = 0;
ratio = R2 / (R1 - R2);
if (R1 < 2 * R2) {
number_of_circles = 1;
}
else {
angle = Math.abs(Math.asin(ratio) * 180)
/ 3.14159265;
number_of_circles = 360
/ (2
* Math.floor(angle));
}
return number_of_circles;
}
let R1 = 3;
let R2 = 1;
document.write(countInscribed(R1, R2))
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...