Prerequisite – Designing finite automata, previous article: Designing Deterministic Finite Automata (Set 1)
In this article, we will see some designing of Deterministic Finite Automata (DFA).
Problem-1: Construction of a DFA for the set of string over {a, b} such that length of the string |w| is divisible by 2 i.e, |w| mod 2 = 0.
Explanation – The desired language will be like:
L = {?, aa, ab, ba, bb, aaaa, bbbb, ............} The state transition diagram of the language will be like:
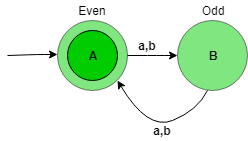
Here, state A represent set of all string of length even (0, 2, 4, …), and state B represent set of all string of length odd (1, 3, 5, …).
Number of states: n
If |W| mod n = 0
def stateA(n):
if(len(n)==0):
print("Accepted")
else:
if (n[0]=='0' or n[0]=='1'):
stateB(n[1:])
def stateB(n):
if(len(n)==0):
print("Not Accepted")
else:
if (n[0]=='0' or n[0]=='1'):
stateA(n[1:])
n=input()
stateA(n)
|
The above automata will accept all the strings having the length of the string divisible by 2. When the length of the string is 1, then it will go from state A to B. When the length of the string is 2, then it will go from state B to A and so on. State A is the final state i.e, it accept all the string having length divisible by 2.
Problem-2: Construction of a DFA for the set of string over {a, b} such that length of the string |w| is not divisible by 2 i.e, |w| mod 2 = 1.
Explanation – The desired language will be like:
L = {a, b, aaa, aab, aba, abb, aaaaa, bbbb, .......} The state transition diagram of the language will be like:
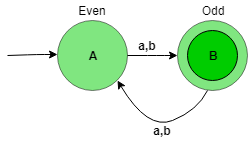
Here, state A represent set of all string of length even (0, 2, 4, …), and state B represent set of all string of length odd (1, 3, 5, …).
def stateA(n):
if(len(n)==0):
print("Not Accepted")
else:
if (n[0]=='0' or n[0]=='1'):
stateB(n[1:])
def stateB(n):
if(len(n)==0):
print("Accepted")
else:
if (n[0]=='0' or n[0]=='1'):
stateA(n[1:])
n=input()
stateA(n)
|
The above automata will accept all the strings having the length of the string not divisible by 2. When the length of the string is 1, then it will go from state A to B. When the length of the string is 2, then it will go from state B to A and so on. State B is the final state i.e, it accept all the string having length not divisible by 2.
Problem-3: Construction of a DFA for the set of string over {a, b} such that length of the string |w| is divisible by 3 i.e, |w| mod 3 = 0.
Explanation – The desired language will be like:
L = {?, aaa, aab, aba, abb, aaaaaa, bbbbbb, .......} The state transition diagram of the language will be like:
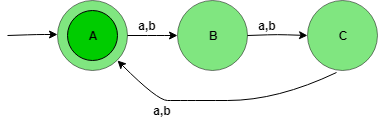
Here, state A represents set for which string’s length divided by 3 then remainder is zero (0), state B represents set for which string’s length divided by 3 then the remainder is one (1), and state C represents set for which string’s length divided by 3 then the remainder is two (2).
Number of states: n
If |W| mod n = 0
def stateA(n):
if(len(n)==0):
print("Accepted")
else:
if (n[0]=='0' or n[0]=='1'):
stateB(n[1:])
def stateB(n):
if(len(n)==0):
print("Not Accepted")
else:
if (n[0]=='0' or n[0]=='1'):
stateC(n[1:])
def stateC(n):
if(len(n)==0):
print("Not Accepted")
else:
if (n[0]=='0' or n[0]=='1'):
stateA(n[1:])
n=input()
stateA(n)
|
The above automata will accept all the strings having the length of the string divisible by 3. When the length of the string is 1, then it will go from state A to B. When the length of the string is 2, then it will go from state B to C and When the length of the string is 3, then it will go from state C to A (final state). State A is the final state i.e, it accepts all the string having the length divisible by 3.
Problem-4: Construction of a DFA for the set of string over {a, b} such that length of the string |w| is not divisible by 3 i.e, |w| mod 3 = 1.
Explanation – The desired language will be like:
L = {a, b, aa, ab, ba, bb, aaaa, bbbb, ........} The state transition diagram of the language will be like:
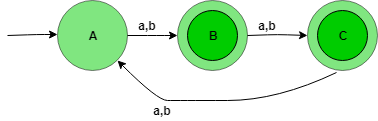
Here, state A represents set for which string’s length divided by 3 then remainder is zero (0), state B represents set for which string’s length divided by 3 then the remainder is one (1), and state C represents set for which string’s length divided by 3 then the remainder is two (2).
def stateA(n):
if(len(n)==0):
print("Not Accepted")
else:
if (n[0]=='0' or n[0]=='1'):
stateB(n[1:])
def stateB(n):
if(len(n)==0):
print("Accepted")
else:
if (n[0]=='0' or n[0]=='1'):
stateC(n[1:])
def stateC(n):
if(len(n)==0):
print("Not Accepted")
else:
if (n[0]=='0' or n[0]=='1'):
stateA(n[1:])
n=input()
stateA(n)
|
The above automata will accept all the strings having the length of the string not divisible by 3. When the length of the string is 1, then it will go from state A to B. When the length of the string is 2, then it will go from state B to C and When the length of the string is 3, then it will go from state C to A. State B and C are the final state i.e, it accepts all the string having the length not divisible by 3.