Ambiguity in Context free Grammar and Context free Languages
Last Updated :
23 Feb, 2022
Prerequisite – Pushdown Automata and Context Free Languages .
Suppose we have a context free grammar G with production rules: S->aSb|bSa|SS|?
Left most derivation (LMD) and Derivation Tree: Leftmost derivation of a string from starting symbol S is done by replacing leftmost non-terminal symbol by RHS of corresponding production rule. For example: The leftmost derivation of string abab from grammar G above is done as:
S => aSb => abSab => abab
The symbols underlined are replaced using production rules.
Derivation tree: It tells how string is derived using production rules from S and has been shown in Figure 1.
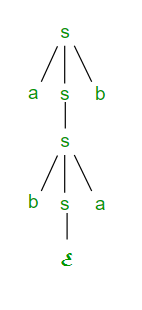
Figure 1
Right most derivation (RMD): Rightmost derivation of a string from starting symbol S is done by replacing rightmost non-terminal symbol by RHS of corresponding production rule. For Example: The rightmost derivation of string abab from grammar G above is done as:
S => SS => SaSb => Sab => aSbab => abab
The symbols underlined are replaced using production rules. The derivation tree for abab using rightmost derivation has been shown in Figure 2.
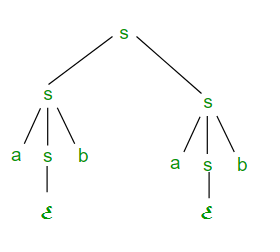
Figure 2
A derivation can be either LMD or RMD or both or none. For Example:
S => aSb => abSab => abab is LMD as well as RMD
but S => SS => SaSb => Sab => aSbab => abab is RMD but not LMD.
Ambiguous Context Free Grammar: A context free grammar is called ambiguous if there exists more than one LMD or more than one RMD for a string which is generated by grammar. There will also be more than one derivation tree for a string in ambiguous grammar. The grammar described above is ambiguous because there are two derivation trees (Figure 1 and Figure 2). There can be more than one RMD for string abab which are:
S => SS => SaSb => Sab => aSbab => abab
S => aSb => abSab => abab
Ambiguous Context Free Languages: A context free language is called ambiguous if there is no unambiguous grammar to define that language and it is also called inherently ambiguous Context Free Languages.
Note:
- If a context free grammar G is ambiguous, language generated by grammar L(G) may or may not be ambiguous
- It is not always possible to convert ambiguous CFG to unambiguous CFG. Only some ambiguous CFG can be converted to unambiguous CFG.
- There is no algorithm to convert ambiguous CFG to unambiguous CFG.
- There always exist a unambiguous CFG corresponding to unambiguous CFL.
- Deterministic CFL are always unambiguous.
Question: Consider the following statements about the context free grammar
G = {S->SS, S->ab, S->ba, S->?}
- I G is ambiguous
- II G produces all strings with equal number of a’s and b’s
- III G can be accepted by a deterministic PDA
Which combination below expresses all the true statements about G?
- I only
- I and III only
- II and III only
- I, II and III
Solution: There are different LMD’s for string abab which can be
S => SS => SSS => abSS => ababS => abab
S => SS => abS => abab
So the grammar is ambiguous. So statement I is true.
Statement II states that the grammar G produces all strings with equal number of a’s and b’s but it can’t generate aabb string. So statement II is incorrect.
Statement III is also correct as it can be accepted by deterministic PDA. So correct option is (B).
Question: Which one of the following statements is FALSE?
- There exist context-free languages such that all the context-free grammars generating them are ambiguous.
- An unambiguous context free grammar always has a unique parse tree for each string of the language generated by it.
- Both deterministic and non-deterministic pushdown automata always accept the same set of languages.
- A finite set of string from one alphabet is always a regular language.
Solution: (A) is correct because for ambiguous CFL’s, all CFG corresponding to it are ambiguous.
(B) is also correct as unambiguous CFG has a unique parse tree for each string of the language generated by it.
(C) is false as some languages are accepted by Non- deterministic PDA but not by deterministic PDA.
(D) is also true as finite set of string is always regular.
So option (C) is correct option.
This article is contributed by Sonal Tuteja.
Share your thoughts in the comments
Please Login to comment...