Chomsky Hierarchy in Theory of Computation

According to Chomsky hierarchy, grammar is divided into 4 types as follows: 

1. Type 0 is known as unrestricted grammar.
2. Type 1 is known as context-sensitive grammar.
3. Type 2 is known as a context-free grammar.
4. Type 3 Regular Grammar.

Type 0: Unrestricted Grammar: 

Type-0 grammars include all formal grammar. Type 0 grammar languages are recognized by turing machine. These languages are also known as the Recursively Enumerable languages. 

Grammar Production in the form of 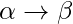   where 

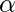 is ( V + T)* V ( V + T)* 
V : Variables 
T : Terminals. 

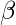 is ( V + T )*. 

In type 0 there must be at least one variable on the Left side of production. 

For example: 

Sab --> ba 
A --> S

Here, Variables are S, A, and Terminals a, b. 

Type 1: Context-Sensitive Grammar

Type-1 grammars generate context-sensitive languages. The language generated by the grammar is recognized by the Linear Bound Automata

In Type 1 

• First of all Type 1 grammar should be Type 0. 
• Grammar Production in the form of 

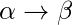
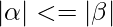
That is the count of symbol in 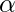is less than or equal to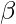 

Also β  ∈ (V + T)⁺

i.e. β can not be ε

For Example:

S --> AB
AB --> abc 
B --> b  

Type 2: Context-Free Grammar: Type-2 grammars generate context-free languages. The language generated by the grammar is recognized by a Pushdown automata.  In Type 2:

• First of all, it should be Type 1. 
• The left-hand side of production can have only one variable and there is no restriction on 

.  

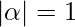For example:

S --> AB 
A --> a 
B --> b 

Type 3: Regular Grammar: Type-3 grammars generate regular languages. These languages are exactly all languages that can be accepted by a finite-state automaton. Type 3 is the most restricted form of grammar. 

Type 3 should be in the given form only : 

V --> VT / T          (left-regular grammar)
(or)
V --> TV /T          (right-regular grammar)

For example:

S --> a

The above form is called strictly regular grammar.

There is another form of regular grammar called extended regular grammar. In this form:

V --> VT* / T*.        (extended left-regular grammar)
(or) 
V --> T*V /T*          (extended right-regular grammar)

For example : 

S --> ab. 

Please write comments if you find anything incorrect, or if you want to share more information about the topic discussed above.