Designing Deterministic Finite Automata (Set 1)
Last Updated :
20 Feb, 2024
C++
#include <iostream>
#include <string>
using namespace std;
int dfa = 0;
void stateA(char n)
{
if ((n == 'a') || (n == 'A') || (n == 'b')
|| (n == 'B'))
dfa = 1;
}
void stateB(char n)
{
if ((n == 'a') || (n == 'A') || (n == 'b')
|| (n == 'B'))
dfa = 2;
}
void stateC(char n)
{
if ((n == 'a') || (n == 'A') || (n == 'b')
|| (n == 'B'))
dfa = 2;
}
bool isAccept(string strr)
{
char* str = new char[strr.length() + 1];
str[strr.length()] = '\0';
for (int i = 0; i < strr.length(); i++) {
str[i] = strr[i];
if (dfa == 0)
stateA(str[i]);
else if (dfa == 1)
stateB(str[i]);
else
stateC(str[i]);
}
return (dfa == 2);
}
int main()
{
string str1 = "a";
if (isAccept(str1) == true)
cout << "Accepted" << endl;
else
cout << "not Accepted" << endl;
string str2 = "abababab";
if (isAccept(str2) == true)
cout << "Accepted" << endl;
else
cout << "not Accepted" << endl;
return 0;
}
|
Java
import java.util.*;
public class Main {
static int dfa = 0;
static void stateA(char n)
{
if ((n == 'a') || (n == 'A') || (n == 'b')
|| (n == 'B'))
dfa = 1;
}
static void stateB(char n)
{
if ((n == 'a') || (n == 'A') || (n == 'b')
|| (n == 'B'))
dfa = 2;
}
static void stateC(char n)
{
if ((n == 'a') || (n == 'A') || (n == 'b')
|| (n == 'B'))
dfa = 2;
}
static boolean isAccept(String strr)
{
char str[] = strr.toCharArray();
for (int i = 0; i < str.length; i++) {
if (dfa == 0)
stateA(str[i]);
else if (dfa == 1)
stateB(str[i]);
else
stateC(str[i]);
}
return (dfa == 2);
}
public static void main(String[] args)
{
String str1 = "a";
if (isAccept(str1) == true)
System.out.println("Accepted");
else
System.out.println("not Accepted");
String str2 = "abababab";
if (isAccept(str2) == true)
System.out.println("Accepted");
else
System.out.println("not Accepted");
}
}
|
Python3
dfa = 0
def stateA(n):
if n.lower() in {'a', 'b'}:
global dfa
dfa = 1
def stateB(n):
if n.lower() in {'a', 'b'}:
global dfa
dfa = 2
def stateC(n):
if n.lower() in {'a', 'b'}:
global dfa
dfa = 2
def is_accept(input_str):
global dfa
for char in input_str:
if dfa == 0:
stateA(char)
elif dfa == 1:
stateB(char)
else:
stateC(char)
return dfa == 2
def main():
str1 = "a"
if is_accept(str1):
print("Accepted")
else:
print("Not Accepted")
str2 = "abababab"
if is_accept(str2):
print("Accepted")
else:
print("Not Accepted")
if __name__ == "__main__":
main()
|
Prerequisite – Designing finite automata In this article, we will see some designing of Deterministic Finite Automata (DFA).
Prob
lem-1: Construction of a DFA for the set of string over {a, b} such that length of the string |w|=2 i.e, length of the string is exactly 2. Explanation – The desired language will be like:
L = {aa, ab, ba, bb}
The state transition diagram of the language will be like: 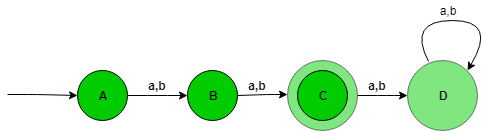 Here, State A represent set of all string of length zero (0), state B represent set of all string of length one (1), state C represent set of all string of length two (2). State C is the final state and D is the dead state it is so because after getting any alphabet as input it will not go into final state ever.
Here, State A represent set of all string of length zero (0), state B represent set of all string of length one (1), state C represent set of all string of length two (2). State C is the final state and D is the dead state it is so because after getting any alphabet as input it will not go into final state ever.
Number of states: n+2
Where n is |w|=n
The above automata will accept all the strings having the length of the string exactly 2. When the length of the string is 1, then it will go from state A to B. When the length of the string is 2, then it will go from state B to C and when the length of the string is greater than 2, then it will go from state C to D (Dead state) and after it from state D TO D itself.
C++
#include <iostream>
#include <string>
void checkStateA(const std::string& n);
void stateB(const std::string& n);
void stateC(const std::string& n);
int main() {
std::string n;
std::cout << "Enter a string: ";
std::cin >> n;
checkStateA(n);
return 0;
}
void checkStateA(const std::string& n) {
if (n.length() == 1) {
std::cout << "string not accepted" << std::endl;
} else {
if (n[0] == 'a' || n[0] == 'b') {
stateB(n.substr(1));
}
}
}
void stateB(const std::string& n) {
if (n.length() != 1) {
std::cout << "string not accepted" << std::endl;
} else {
stateC(n.substr(1));
}
}
void stateC(const std::string& n) {
if (n.empty()) {
std::cout << "string accepted" << std::endl;
} else {
std::cout << "string not accepted" << std::endl;
}
}
|
Java
import java.util.Scanner;
public class StateMachine {
public static void main(String[] args) {
String inputString = "aa";
checkStateA(inputString);
}
static void checkStateA(String n) {
if (n.length() == 1) {
System.out.println("string not accepted");
} else {
if (n.charAt(0) == 'a' || n.charAt(0) == 'b') {
stateB(n.substring(1));
}
}
}
static void stateB(String n) {
if (n.length() != 1) {
System.out.println("string not accepted");
} else {
stateC(n.substring(1));
}
}
static void stateC(String n) {
if (n.isEmpty()) {
System.out.println("string accepted");
} else {
System.out.println("string not accepted");
}
}
}
|
Python3
def checkStateA(n):
if(len(n)==1):
print("string not accepted")
else:
if(n[0]=='a' or n[0]=='b'):
stateB(n[1:])
def stateB(n):
if(len(n)!=1):
print("string not accepted")
else:
stateC(n[1:])
def stateC(n):
if (len(n)==0):
print("string accepted")
else:
print("string not accepted")
n=input()
checkStateA(n)
|
C#
using System;
class StateMachine
{
static void Main()
{
string inputString = "aa";
CheckStateA(inputString);
}
static void CheckStateA(string n)
{
if (n.Length == 1)
{
Console.WriteLine("string not accepted");
}
else
{
if (n[0] == 'a' || n[0] == 'b')
{
StateB(n.Substring(1));
}
}
}
static void StateB(string n)
{
if (n.Length != 1)
{
Console.WriteLine("string not accepted");
}
else
{
StateC(n.Substring(1));
}
}
static void StateC(string n)
{
if (string.IsNullOrEmpty(n))
{
Console.WriteLine("string accepted");
}
else
{
Console.WriteLine("string not accepted");
}
}
}
|
Javascript
function checkStateA(n) {
if (n.length === 1) {
console.log("string not accepted");
} else {
if (n[0] === 'a' || n[0] === 'b') {
stateB(n.substring(1));
}
}
}
function stateB(n) {
if (n.length !== 1) {
console.log("string not accepted");
} else {
stateC(n.substring(1));
}
}
function stateC(n) {
if (n.length === 0) {
console.log("string accepted");
} else {
console.log("string not accepted");
}
}
function main() {
const readline = require('readline');
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
rl.question("Enter a string: ", function (n) {
checkStateA(n);
rl.close();
});
}
main();
|
Problem-2: Construction of a DFA for the set of string over {a, b} such that length of the string |w|>=2 i.e, length of the string should be at least 2. Explanation – The desired language will be like:
L = {aa, ab, ba, bb, aaa, aab, aba, abb........}
The state transition diagram of the language will be like:  Here, State A represent set of all string of length zero (0), state B represent set of all string of length one (1), and state C represent set of all string of length two (2).
Here, State A represent set of all string of length zero (0), state B represent set of all string of length one (1), and state C represent set of all string of length two (2).
Number of states: n+1
Where n is |w|>=n
The above automata will accept all the strings having the length of the string at least 2. When the length of the string is 1, then it will go from state A to B. When the length of the string is 2, then it will go from state B to C and lastly when the length of the string is greater than 2, then it will go from state C to C itself.
Python3
def checkStateA(n):
if(len(n)==1):
print("string not accepted")
else:
if(n[0]=='a' or n[0]=='b'):
stateB(n[1:])
def stateB(n):
if(len(n)<1):
print("string not accepted")
else:
stateC(n[1:])
def stateC(n):
if (len(n)>=0):
print("string accepted")
else:
print("string not accepted")
n=input()
checkStateA(n)
|
Problem-3: Construction of a DFA for the set of string over {a, b} such that length of the string |w|<=2 i.e, length of the string is atmost 2.
Explanation – The desired language will be like:
L = {?, aa, ab, ba, bb}
The state transition diagram of the language will be like: 
Here, State A represent set of all string of length zero (0), state B represent set of all string of length one (1), state C represent set of all string of length two (2), state A, B, C is the final state and D is the dead state it is so because after getting any alphabet as input it will not go into final state ever.
Number of states: n+2
Where n is |w|<=n
The above automata will accept all the strings having the length of the string at most 2. When the length of the string is 1, then it will go from state A to B. When the length of the string is 2, then it will go from state B to C and lastly when the length of the string is greater than 2, then it will go from state C to D (Dead state).
Python3
def checkStateA(n):
if(n[0]=='a' or n[0]=='b'):
stateB(n[1:])
def stateB(n):
if(len(n)==0):
print("string accepted")
else:
stateC(n[1:])
def stateC(n):
if (len(n)==0):
print("string accepted")
else:
print("string not accepted")
n=input()
checkStateA(n)
|
Share your thoughts in the comments
Please Login to comment...