Kleene’s Theorem in TOC | Part-1
Last Updated :
04 Sep, 2023
A language is said to be regular if it can be represented by using Finite Automata or if a Regular Expression can be generated for it. This definition leads us to the general definition that; For every Regular Expression corresponding to the language, a Finite Automata can be generated.
For certain expressions like:- (a+b), ab, (a+b)*; It’s fairly easier to make the Finite Automata by just intuition as shown below. The problem arises when we are provided with a longer Regular Expression. This brings about the need for a systematic approach towards Finite Automata generation, which Kleene has put forward in Kleene’s Theorem.
For any Regular Expression r that represents Language L(r), there is a Finite Automata that accepts same language.

Regular Expression
To understand Kleene’s Theorem-I, Let’s take into account the basic definition of Regular Expression where we observe that 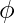 ,
, 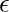 and a single input symbol “a” can be included in a Regular Language and the corresponding operations that can be performed by the combination of these are: Say,
and a single input symbol “a” can be included in a Regular Language and the corresponding operations that can be performed by the combination of these are: Say, 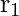 and
and 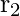 be two regular expressions. Then,
be two regular expressions. Then,
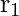 +
+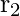 is a regular expression too, whose corresponding language is L(
is a regular expression too, whose corresponding language is L(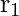 ) U L(
) U L(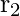 )
)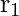 .
.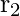 is a regular expression too, whose corresponding language is L(
is a regular expression too, whose corresponding language is L(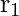 ).L(
).L(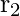 )
)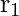 * is a regular expression too, whose corresponding language is L(
* is a regular expression too, whose corresponding language is L(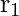 )*
)*
Observations From Kleene Theorem
We can further use this definition in association with Null Transitions to give rise to a FA by the combination of two or smaller Finite Automata (each corresponding to a Regular Expression). Let S accept L = {a} and T accept L = {b}, then R can be represented as a combination of S and T using the provided operations:
Union Operation
R = S + T

Union Operation
Observations:
- In the case of union operation, we can have a new start state, from which, the null transition proceeds to the starting state of both the Finite State Machines.
- The final states of both the Finite Automata are converted to intermediate states. The final state is unified into one which can be traversed by null transitions.
Concatenation Operation
R = S.T

Concatenation Operation
Observations:
- In the case of a concatenation operation we can have the same starting state as that of S, the only change occurs in the end state of S, which is converted to an intermediate state followed by a Null Transition.
- The Null transition is followed by the starting state of T, and the final state of T is used as the end state of R.
Exponential Operation
R = S*

Exponential Operation
Observations:
- A new starting state is added, and S has been put as an intermediate state so that the self-looping condition could be incorporated.
- Starting and Ending states have been defined separately so that the self-looping condition is not disturbed.
Now that we are aware of the general operations. Let’s see how Kleene’s Theorem-I can be used to generate a FA for the given Regular Expression.
Example: Make a Finite Automata for the expression (ab+a)*

Kleene Algorithm
We see that using Kleene’s Theorem – Gives a systematic approach towards the generation of Finite Automata for the provided Regular Expression.
FAQs on Kleene’s Theorem
Q. 1: Does Kleene Theoram only restricted to Turing Machine?
Answer:
Kleene Theoram is primarily for Turing Machines only, but some similar self reference concepts can be formed in other machine models also.
Q. 2: Is it possible to implement Kleene Theoram practically?
Answer:
Kleene Theoram is basically a theoretical concept that does not have any direct practical applications. Computer Scientists understand the boundations, limitations with respect to this algorithm.
Q. 3: Is there any relation between Kleene Theoram and Halting Algorithm?
Answer:
Kleene Theoram and Halting Problem are closely related to each other as these both concepts involve self-reference and highlight the algorithmic solution limitation.
Share your thoughts in the comments
Please Login to comment...