Check if the language is Context Free or Not
Last Updated :
10 Aug, 2018
Prerequisite –
Pumping Lemma,
How to identify if a language is regular or not
We typically face questions to identify which of the given languages are context free. In case of regular languages, it is comparatively easy to answer this, but for Context Free languages, it is tricky sometimes. Pumping Lemma provides us with ability to perform negative test, i.e. if a language doesn’t satisfy pumping lemma, then we can definitely say that it is not context free, but if it satisfies, then the language may or may not be context free. Pumping Lemma is more of a mathematical proof, takes more time and to apply it on context free languages is a tedious task and finding out counter example for complex language expressions is not much handful. We can address this problem very quickly, based on common observations and analysis:
- Every regular language is context free.
Example – {
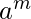
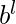
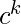
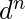 | m, l, k, n >= 1 } is context free, as it is regular too.
| m, l, k, n >= 1 } is context free, as it is regular too.
- Given an expression such that it is possible to obtain a center or mid point in the strings, so we can carry out comparison of left and right sub-parts using stack.
Example 1 – L = {
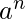
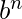 | n >= 1} is context free, as we can push a’s and then we can pop a’s for each occurrence of b.
Example 2 – L = {
| n >= 1} is context free, as we can push a’s and then we can pop a’s for each occurrence of b.
Example 2 – L = { 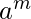
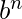
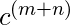 } is context free. We can rewrite it as {
} is context free. We can rewrite it as { 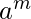
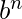
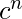
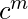 }.
Example 3 – L = {
}.
Example 3 – L = { 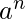
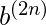 } is context free, as we can push two a’s and pop an a for each occurrence of b. Hence, we get a mid-point here as well.
Example 4 – L = {
} is context free, as we can push two a’s and pop an a for each occurrence of b. Hence, we get a mid-point here as well.
Example 4 – L = { 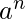
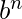
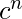 } is not context free.
} is not context free.
- Given expression is a combination of multiple expressions with mid-points in them, such that each sub-expression is independent of other sub-expressions, then it is context free.
Example 1 – L = {
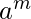
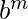
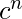
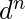 } is context free. It contains multiple expressions with a mid-point in each of them.
Example 2 – L = {
} is context free. It contains multiple expressions with a mid-point in each of them.
Example 2 – L = { 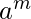
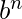
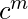
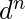 } is not context free.
} is not context free.
- Given expression consists of an operation where mid-point could be found along with some independent regular expressions in between, results into context free language.
Example – L = {
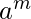
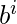
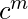
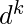 } is a context free language.
Here, we have b^i and d^k as independent regular expressions in between, which doesn’t affect the stack.
} is a context free language.
Here, we have b^i and d^k as independent regular expressions in between, which doesn’t affect the stack.
- An expression that doesn’t form a pattern on which linear comparison could be carried out using stack is not context free language.
Example 1 – L = { a^m b^n^2 } is not context free.
Example 2 – L = { a^n b^2^n } is not context free.
Example 3 – L = { a^n^2 } is not context free.
Example 4 – L = {
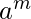 | m is prime } is not context free.
| m is prime } is not context free.
- An expression that involves counting and comparison of three or more variables independently is not context free language, as stack allows comparison of only two variables at a time.
Example 1 – L = {
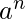
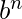
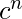 } is not context free.
Example 2 – L = { w | na(w) = nb(w) = nc(w) } is not context free.
Example 3 – L = {
} is not context free.
Example 2 – L = { w | na(w) = nb(w) = nc(w) } is not context free.
Example 3 – L = { 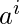
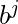
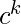 | i > j > k } is not context free.
| i > j > k } is not context free.
- A point to remember is counting and comparison could only be done with the top of stack and not with bottom of stack in Push Down Automata, hence a language exhibiting a characteristic that involves comparison with bottom of stack is not a context free language.
Example 1 – L = {
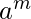
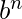
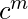
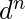 } is not context free.
Pushing a’s first then b’s. Now, we will not be able to compare c’s with a’s as the top of the stack has b’s.
Example 2 – L = { WW | W belongs to {a, b}* } is not context free.
One might think to draw a non-deterministic push down automaton, but it will not help as first symbol will be at bottom of the stack and when the second W starts, we will not be able to compare it with the bottom of stack.
} is not context free.
Pushing a’s first then b’s. Now, we will not be able to compare c’s with a’s as the top of the stack has b’s.
Example 2 – L = { WW | W belongs to {a, b}* } is not context free.
One might think to draw a non-deterministic push down automaton, but it will not help as first symbol will be at bottom of the stack and when the second W starts, we will not be able to compare it with the bottom of stack.
- If we can find mid-point in the expression even in a non-deterministic way, then it is context free language.
Example 1 – L = { W
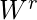 | W belongs to {a, b}* } is context free language.
Example 2 – L = {
| W belongs to {a, b}* } is context free language.
Example 2 – L = { 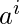
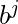
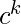
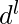 | i=k or j=l } is a context free language.
| i=k or j=l } is a context free language.
Share your thoughts in the comments
Please Login to comment...