Having gained the knowledge of how to draw a basic Finite State Machine ( DFA, NFA or 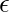 -NFA ). We head to deriving a Regular Expression from the provided state machine.
-NFA ). We head to deriving a Regular Expression from the provided state machine.
For certain examples provided below, it’s fairly simple to derive them.

But for the following example, it’s fairly hard to derive the Regular Expression by just observing the Finite State Machine. For this purpose, we make use of Arden’s Theorem to simplify our Individual State Equations and come up with our final state equation ( which may or may not be the simplified version)

Arden’s Theorem states that, if P & Q are two regular expressions over 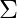 , and if P does not contain
, and if P does not contain 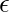 , then the following equation R given by R = Q + RP has a unique solution ; R = QP*
, then the following equation R given by R = Q + RP has a unique solution ; R = QP*
PROOF :-
R = Q + RP
R = Q + QP*P ( Substituting the value of R )
R = Q(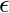 + P*P)R = QP *( P*P =
+ P*P)R = QP *( P*P = 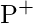 ,
, 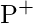 +
+ 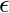 = P* )
= P* )
Let’s solve the provided automata above with the help of Arden’s Theorem.
We see, that on state C, there is a state transition coming from B when a is the input
C = Ba
On state B, There is a self loop on input b, a transition from A when input is a, a transition from state C when input is b
B = Bb + Cb + Aa
On state A, There is a 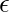 transition ( being the start state,
transition ( being the start state, 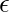 transition must be included), a self loop on input a, a transition from B when input is b.
transition must be included), a self loop on input a, a transition from B when input is b.
A = 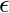 + Aa + Bb
+ Aa + Bb
Putting (2) in (1), we get
C = Ba
C = (Aa + Bb + Cb)a
C = Aaa + Bba + Cba
Putting (1) in (2), we get
B = Bb + Cb + Aa
B = Aa + Bb + (Ba)b
B = Aa + B(b + ab)
B = Aa(b + ab)* (Using R = QP*)
Putting (2) in (3), we get
A = 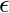 [Tex]+ Aa + Bb[/Tex]A =
[Tex]+ Aa + Bb[/Tex]A = 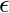 [Tex]+ Aa + Aa(b + ab)*b[/Tex]A =
[Tex]+ Aa + Aa(b + ab)*b[/Tex]A = 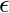 [Tex]+ A(a + a(b + ab)*b)[/Tex]A =
[Tex]+ A(a + a(b + ab)*b)[/Tex]A = 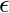 [Tex](a + a(b + ab)*b)*[/Tex]A = (a + a(b + ab)*b)*
[Tex](a + a(b + ab)*b)*[/Tex]A = (a + a(b + ab)*b)*
As a final step, Let’s combine all the simplified equations onto the final state C
C = Ba
C = Aa(b + ab)*a
C = (a + a(b + ab)*b)* a (b + ab)* a
Now, this example corresponded to direct derivation from a provided NFA to a Regular Expression.
STEPS TO CONVERT NFA/DFA TO RE:
- Let N be the given NFA/DFA with a state and transition without ε (epsilon).
- Now, write the transition function for every state [which contains incoming symbols and the state]
- Using reverse substitution method find the equation i.e. RE for the final state.
Let’s say, we are provided with a problem’s that goes like –
Problem 1: Derive a regular expression to represent a language having even no. of a’s
For this case, it’s difficult to arrive at a regular expression with just trial and error methodology.
We might come across sample solutions like :-
which might satisfy some cases, but also leads to unwanted cases and missing cases with alternate a’s and b’s.
The best way to solve this problem is to first draw a finite state machine for the same, and then derive the regular expression from the same.
The figure below shows the DFA for the provided problem

Now that we have the DFA, let’s solve it using Arden’s Theorem of Individual State Equations.
We see that on state A, there is a self loop with input b and transition from B with input a
A = 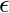 [Tex]+ Ab + Ba[/Tex]
[Tex]+ Ab + Ba[/Tex]
We see that on state B, there is a self loop on input b and transition from A when input is a.
B = Aa + Bb
Taking equation for B, we can apply Arden’s theorem
B = Aa + Bb
B = Aab*
Substituting the value of B in A we get
A = 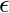 [Tex]+ Ab + Ba[/Tex]A =
[Tex]+ Ab + Ba[/Tex]A = 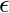 [Tex]+ Ab + (Aab*)a[/Tex]A =
[Tex]+ Ab + (Aab*)a[/Tex]A = 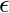 [Tex]( b + ab*a )*[/Tex]A = ( b + ab*a )*
[Tex]( b + ab*a )*[/Tex]A = ( b + ab*a )*
Hence, the regular expression for the provided problem is RE : ( b + ab*a )*
We see that Arden’s theorem can be used as a powerful simplification tool to determine the Regular Expressions and also to design the desired Finite State Machine from the same.
Please refer for Set 1
Problem 2: Construct R.E for the given NFA/DFA
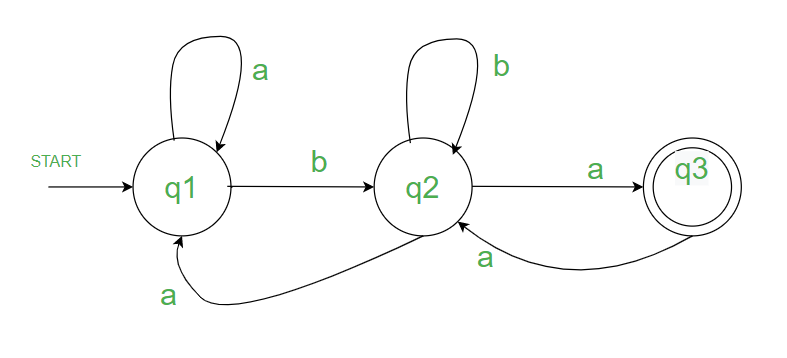
Problem 2
SOLUTION:
q1 if the start state and the double circle i.e. q3 indicates final state.
First write all the states and write all the incoming states to that particular state along with the input signal (step 2) i.e.
on,
q1 = q1.a + q2.a + ε (start symbol epsilon)
q2 = q1.b + q2.b + q3.a
q3 = q2.a
[NOTE: SO FROM THE ABOVE THREE STATES WE NEED TO FIND THE EQUATION FOR FINAL STATE i.e. q3 TO GET THE R.E FROM THE GIVEN NFA/DFA]
Now using reverse substitution method.
Substituting, q3 in q2 i.e. q2 will now become
q2 = q1.b + q2.b + q2.aa ———————->(subst. q3 in q2)
Now taking q2 common, that will be
q2 = q1.b + q2[b+aa]
Applying ARDEN’S THEOREM as shown in fig.(EXAMPLE 2.1)
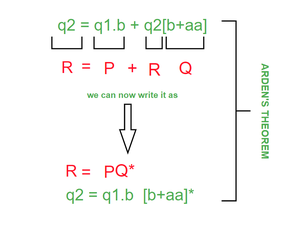
EXAMPLE 2.1
q2 = q1.b [b+aa]* ——————————–(equation 1)
Now, Substituting equation 1 in q1
q1 = q1.a + q1.b [b+aa]* a + ε
Now, taking q1 common,
q1 = q1. [a + b (b+aa)* a] + ε
Applying ARDEN’S THEOREM as shown in fig.(EXAMPLE 2.2)

EXAMPLE 2.2
q1 = [a + b (b+aa)* a]* ——————————–(equation 2)
As there is no use of ε (epsilon) we can simply remove it from our equation as shown above.
Now, Substituting equation 2 in q2,
q2 = [a + b (b+aa)* a]* b (b+aa)* ——————————–(equation 3)
Now, Substituting equation 3 in q3 to get our final answer,
q3 = [a + b (b+aa)* a]* b (b+aa)* a
FINAL ANSWER: q3 = [a + b (b+aa)* a]* b (b+aa)* a
Advantages of Arden’s Theorem:
Simple and systematic solution: Arden’s theorem offers a straightforward and systematic approach to finding the solution to a system of equations involving regular expressions. It provides a step-by-step procedure that can be followed to compute the unique solution efficiently.
Applicability to regular languages: Arden’s theorem is specifically designed for regular languages and regular expressions. It is particularly useful when dealing with problems related to regular languages, such as constructing finite automata, defining lexical analyzers, or solving regular expression-based pattern matching problems.
Guarantees uniqueness of solutions: Arden’s theorem guarantees that the system of equations has a unique solution, given that the equations satisfy certain conditions. This uniqueness property ensures that the computed solution is unambiguous and reliable for the given system of equations.
Disadvantages of Arden’s Theorem:
Limited to regular expressions: Arden’s theorem is limited in its applicability to regular expressions and regular languages. It cannot be directly used for solving systems of equations involving more complex formalisms, such as context-free or context-sensitive grammars.
May not apply to all cases: Arden’s theorem relies on certain conditions being satisfied by the system of equations. In some cases, these conditions may not be met, making the theorem inapplicable. It is essential to ensure that the system of equations conforms to the required properties for Arden’s theorem to be effectively used.
Computationally expensive: While Arden’s theorem provides a systematic solution, it may involve computationally expensive steps for large systems of equations. The process of iteratively substituting and simplifying equations can become time-consuming and resource-intensive, particularly when dealing with complex regular expressions or a significant number of equations.
Limited expressive power: Arden’s theorem is specifically designed for regular languages and regular expressions, which have limited expressive power compared to more complex language classes. It cannot be used to solve equations involving context-free or context-sensitive languages, which require more powerful computational models.
Share your thoughts in the comments
Please Login to comment...