Cycles of length n in an undirected and connected graph
Last Updated :
27 Jan, 2023
Given an undirected and connected graph and a number n, count total number of cycles of length n in the graph. A cycle of length n simply means that the cycle contains n vertices and n edges. And we have to count all such cycles that exist.
Example :
Input : n = 4
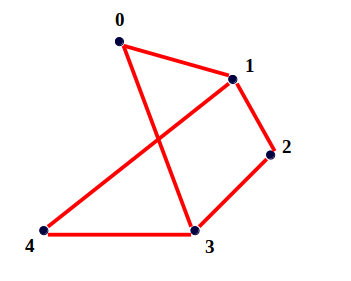
Output : Total cycles = 3
Explanation : Following 3 unique cycles
0 -> 1 -> 2 -> 3 -> 0
0 -> 1 -> 4 -> 3 -> 0
1 -> 2 -> 3 -> 4 -> 1
Note* : There are more cycles but
these 3 are unique as 0 -> 3 -> 2 -> 1
-> 0 and 0 -> 1 -> 2 -> 3 -> 0 are
same cycles and hence will be counted as 1.
To solve this Problem, DFS(Depth First Search) can be effectively used. Using DFS we find every possible path of length (n-1) for a particular source (or starting point). Then we check if this path ends with the vertex it started with, if yes then we count this as the cycle of length n. Notice that we looked for path of length (n-1) because the nth edge will be the closing edge of cycle.
Every possible path of length (n-1) can be searched using only V – (n – 1) vertices (where V is the total number of vertices).
For above example, all the cycles of length 4 can be searched using only 5-(4-1) = 2 vertices. The reason behind this is quite simple, because we search for all possible path of length (n-1) = 3 using these 2 vertices which include the remaining 3 vertices. So, these 2 vertices cover the cycles of remaining 3 vertices as well, and using only 3 vertices we can’t form a cycle of length 4 anyways.
One more thing to notice is that, every vertex finds 2 duplicate cycles for every cycle that it forms. For above example 0th vertex finds two duplicate cycle namely 0 -> 3 -> 2 -> 1 -> 0 and 0 -> 1 -> 2 -> 3 -> 0. Hence the total count must be divided by 2 because every cycle is counted twice.
Implementation:
C++
#include <bits/stdc++.h>
using namespace std;
const int V = 5;
void DFS(bool graph[][V], bool marked[], int n, int vert,
int start, int& count)
{
marked[vert] = true;
if (n == 0) {
marked[vert] = false;
if (graph[vert][start] && graph[start][vert]) {
count++;
return;
}
else
return;
}
for (int i = 0; i < V; i++)
if (!marked[i] && graph[vert][i])
DFS(graph, marked, n - 1, i, start, count);
marked[vert] = false;
}
int countCycles(bool graph[][V], int n)
{
bool marked[V];
memset(marked, 0, sizeof(marked));
int count = 0;
for (int i = 0; i < V - (n - 1); i++) {
DFS(graph, marked, n - 1, i, i, count);
marked[i] = true;
}
return count / 2;
}
int main()
{
bool graph[][V] = { { 0, 1, 0, 1, 0 },
{ 1, 0, 1, 0, 1 },
{ 0, 1, 0, 1, 0 },
{ 1, 0, 1, 0, 1 },
{ 0, 1, 0, 1, 0 } };
int n = 4;
cout << "Total cycles of length " << n << " are "
<< countCycles(graph, n);
return 0;
}
|
Java
public class Main {
public static final int V = 5;
static int count = 0;
static void DFS(int graph[][], boolean marked[],
int n, int vert, int start) {
marked[vert] = true;
if (n == 0) {
marked[vert] = false;
if (graph[vert][start] == 1) {
count++;
return;
} else
return;
}
for (int i = 0; i < V; i++)
if (!marked[i] && graph[vert][i] == 1)
DFS(graph, marked, n-1, i, start);
marked[vert] = false;
}
static int countCycles(int graph[][], int n) {
boolean marked[] = new boolean[V];
for (int i = 0; i < V - (n - 1); i++) {
DFS(graph, marked, n-1, i, i);
marked[i] = true;
}
return count / 2;
}
public static void main(String[] args) {
int graph[][] = {{0, 1, 0, 1, 0},
{1, 0, 1, 0, 1},
{0, 1, 0, 1, 0},
{1, 0, 1, 0, 1},
{0, 1, 0, 1, 0}};
int n = 4;
System.out.println("Total cycles of length "+
n + " are "+
countCycles(graph, n));
}
}
|
Python3
V = 5
def DFS(graph, marked, n, vert, start, count):
marked[vert] = True
if n == 0:
marked[vert] = False
if graph[vert][start] == 1:
count = count + 1
return count
else:
return count
for i in range(V):
if marked[i] == False and graph[vert][i] == 1:
count = DFS(graph, marked, n-1, i, start, count)
marked[vert] = False
return count
def countCycles( graph, n):
marked = [False] * V
count = 0
for i in range(V-(n-1)):
count = DFS(graph, marked, n-1, i, i, count)
marked[i] = True
return int(count/2)
graph = [[0, 1, 0, 1, 0],
[1 ,0 ,1 ,0, 1],
[0, 1, 0, 1, 0],
[1, 0, 1, 0, 1],
[0, 1, 0, 1, 0]]
n = 4
print("Total cycles of length ",n," are ",countCycles(graph, n))
|
C#
using System;
class GFG
{
public static int V = 5;
static int count = 0;
static void DFS(int [,]graph, bool []marked,
int n, int vert, int start)
{
marked[vert] = true;
if (n == 0)
{
marked[vert] = false;
if (graph[vert, start] == 1)
{
count++;
return;
}
else
return;
}
for (int i = 0; i < V; i++)
if (!marked[i] && graph[vert, i] == 1)
DFS(graph, marked, n - 1, i, start);
marked[vert] = false;
}
static int countCycles(int [,]graph, int n)
{
bool []marked = new bool[V];
for (int i = 0; i < V - (n - 1); i++)
{
DFS(graph, marked, n - 1, i, i);
marked[i] = true;
}
return count / 2;
}
public static void Main()
{
int [,]graph = {{0, 1, 0, 1, 0},
{1, 0, 1, 0, 1},
{0, 1, 0, 1, 0},
{1, 0, 1, 0, 1},
{0, 1, 0, 1, 0}};
int n = 4;
Console.WriteLine("Total cycles of length "+
n + " are "+
countCycles(graph, n));
}
}
|
Javascript
<script>
var V = 5;
var count = 0;
function DFS(graph, marked, n, vert, start)
{
marked[vert] = true;
if (n == 0)
{
marked[vert] = false;
if (graph[vert][start] == 1)
{
count++;
return;
}
else
return;
}
for (var i = 0; i < V; i++)
if (!marked[i] && graph[vert][i] == 1)
DFS(graph, marked, n - 1, i, start);
marked[vert] = false;
}
function countCycles(graph, n)
{
var marked = Array(V).fill(false);
for (var i = 0; i < V - (n - 1); i++)
{
DFS(graph, marked, n - 1, i, i);
marked[i] = true;
}
return parseInt(count / 2);
}
var graph = [[0, 1, 0, 1, 0],
[1, 0, 1, 0, 1],
[0, 1, 0, 1, 0],
[1, 0, 1, 0, 1],
[0, 1, 0, 1, 0]];
var n = 4;
document.write("Total cycles of length "+
n + " are "+
countCycles(graph, n));
</script>
|
Output
Total cycles of length 4 are 3
Time Complexity: O(V*V)
Space Complexity: O(V)
Share your thoughts in the comments
Please Login to comment...