Program to count Number of connected components in an undirected graph
Last Updated :
03 Apr, 2023
Given an undirected graph g, the task is to print the number of connected components in the graph.
Examples:
Input:
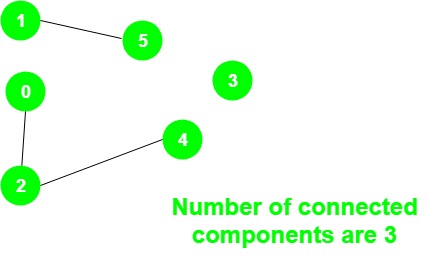
Output: 3
There are three connected components:
1 – 5, 0 – 2 – 4 and 3
Approach:
DFS visit all the connected vertices of the given vertex.
When iterating over all vertices, whenever we see unvisited node, it is because it was not visited by DFS done on vertices so far.
That means it is not connected to any previous nodes visited so far i.e it was not part of previous components.
Hence this node belongs to new component.
This means, before visiting this node, we just finished visiting all nodes previous component and that component is now complete.
So we need to increment component counter as we completed a component.
The idea is to use a variable count to store the number of connected components and do the following steps:
Initialize all vertices as unvisited.
For all the vertices check if a vertex has not been visited, then perform DFS on that vertex and increment the variable count by 1.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
class Graph {
int V;
list<int>* adj;
void DFSUtil(int v, bool visited[]);
public:
Graph(int V);
void addEdge(int v, int w);
int NumberOfconnectedComponents();
};
int Graph::NumberOfconnectedComponents()
{
bool* visited = new bool[V];
int count = 0;
for (int v = 0; v < V; v++)
visited[v] = false;
for (int v = 0; v < V; v++) {
if (visited[v] == false) {
DFSUtil(v, visited);
count += 1;
}
}
return count;
}
void Graph::DFSUtil(int v, bool visited[])
{
visited[v] = true;
list<int>::iterator i;
for (i = adj[v].begin(); i != adj[v].end(); ++i)
if (!visited[*i])
DFSUtil(*i, visited);
}
Graph::Graph(int V)
{
this->V = V;
adj = new list<int>[V];
}
void Graph::addEdge(int v, int w)
{
adj[v].push_back(w);
adj[w].push_back(v);
}
int main()
{
Graph g(5);
g.addEdge(1, 0);
g.addEdge(2, 3);
g.addEdge(3, 4);
cout << g.NumberOfconnectedComponents();
return 0;
}
|
Java
import java.util.*;
class Graph {
private int V;
private LinkedList<Integer>[] adj;
ArrayList<ArrayList<Integer> > components
= new ArrayList<>();
@SuppressWarnings("unchecked") Graph(int v)
{
V = v;
adj = new LinkedList[v];
for (int i = 0; i < v; i++)
adj[i] = new LinkedList();
}
void addEdge(int u, int w)
{
adj[u].add(w);
adj[w].add(u);
}
void DFSUtil(int v, boolean[] visited,
ArrayList<Integer> al)
{
visited[v] = true;
al.add(v);
System.out.print(v + " ");
Iterator<Integer> it = adj[v].iterator();
while (it.hasNext()) {
int n = it.next();
if (!visited[n])
DFSUtil(n, visited, al);
}
}
void DFS()
{
boolean[] visited = new boolean[V];
for (int i = 0; i < V; i++) {
ArrayList<Integer> al = new ArrayList<>();
if (!visited[i]) {
DFSUtil(i, visited, al);
components.add(al);
}
}
}
int ConnectedComponents() { return components.size(); }
}
public class Main {
public static void main(String[] args)
{
Graph g = new Graph(6);
g.addEdge(1, 5);
g.addEdge(0, 2);
g.addEdge(2, 4);
System.out.println("Graph DFS:");
g.DFS();
System.out.println(
"\nNumber of Connected Components: "
+ g.ConnectedComponents());
}
}
|
Python3
class Graph:
def __init__(self, V):
self.V = V
self.adj = [[] for i in range(self.V)]
def NumberOfconnectedComponents(self):
visited = [False for i in range(self.V)]
count = 0
for v in range(self.V):
if (visited[v] == False):
self.DFSUtil(v, visited)
count += 1
return count
def DFSUtil(self, v, visited):
visited[v] = True
for i in self.adj[v]:
if (not visited[i]):
self.DFSUtil(i, visited)
def addEdge(self, v, w):
self.adj[v].append(w)
self.adj[w].append(v)
if __name__=='__main__':
g = Graph(5)
g.addEdge(1, 0)
g.addEdge(2, 3)
g.addEdge(3, 4)
print(g.NumberOfconnectedComponents())
|
C#
using System;
using System.Collections.Generic;
class Graph
{
int V;
List<int>[] adj;
public Graph(int v)
{
V = v;
adj = new List<int>[ V ];
for (int i = 0; i < V; i++) {
adj[i] = new List<int>();
}
}
public void addEdge(int v, int w)
{
adj[v].Add(w);
adj[w].Add(v);
}
private void DFSUtil(int v, bool[] visited)
{
visited[v] = true;
foreach(int i in adj[v])
{
if (!visited[i]) {
DFSUtil(i, visited);
}
}
}
public int NumberOfConnectedComponents()
{
bool[] visited = new bool[V];
int count = 0;
for (int v = 0; v < V; v++) {
if (!visited[v]) {
DFSUtil(v, visited);
count++;
}
}
return count;
}
}
class Program {
static void Main(string[] args)
{
Graph g = new Graph(5);
g.addEdge(1, 0);
g.addEdge(2, 3);
g.addEdge(3, 4);
Console.WriteLine(g.NumberOfConnectedComponents());
}
}
|
Javascript
<script>
class Graph{
constructor(V){
this.V = V
this.adj = new Array(this.V);
for(let i=0;i<V;i++){
this.adj[i] = new Array()
}
}
NumberOfconnectedComponents(){
let visited = new Array(this.V).fill(false);
let count = 0
for(let v=0;v<this.V;v++){
if (visited[v] == false){
this.DFSUtil(v, visited)
count += 1
}
}
return count
}
DFSUtil(v, visited){
visited[v] = true;
for(let i of this.adj[v]){
if (visited[i] == false){
this.DFSUtil(i, visited)
}
}
}
addEdge(v, w){
this.adj[v].push(w)
this.adj[w].push(v)
}
}
let g = new Graph(5)
g.addEdge(1, 0)
g.addEdge(2, 3)
g.addEdge(3, 4)
document.write(g.NumberOfconnectedComponents(),"</br>")
</script>
|
Complexity Analysis:
Time complexity: O(V + E), where V is the number of vertices and E is the number of edges in the graph.
Space Complexity: O(V), since an extra visited array of size V is required.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...