Count Unique Paths in matrix

The problem is to count all unique possible paths from the top left to the bottom right of a M X N matrix with the constraints that from each cell you can either move only to the right or down

Examples:

Input: M = 2, N = 2
Output: 2
Explanation: There are two paths
(0, 0) -> (0, 1) -> (1, 1)
(0, 0) -> (1, 0) -> (1, 1)
Input: M = 2, N = 3
Output: 3
Explanation: There are three paths
(0, 0) -> (0, 1) -> (0, 2) -> (1, 2)
(0, 0) -> (0, 1) -> (1, 1) -> (1, 2)
(0, 0) -> (1, 0) -> (1, 1) -> (1, 2)

Count all possible paths from top left to the bottom right of a M X N matrix using Recursion:

To solve the problem follow the below idea:

We can recursively move to right and down from the start until we reach the destination and then add up all valid paths to get the answer.

Follow the below steps to solve the problem:

Create a recursive function with parameters as row and column index
Call this recursive function for N-1 and M-1
In the recursive function
- If N == 1 or M == 1 then return 1
- else call the recursive function with (N-1, M) and (N, M-1) and return the sum of this
Print the answer

Below is the implementation of the above approach:

C++

// A C++  program to count all possible paths
// from top left to bottom right
 
#include <bits/stdc++.h>
using namespace std;
 
// Returns count of possible paths to reach cell at row
// number m and column number n from the topmost leftmost
// cell (cell at 1, 1)
int numberOfPaths(int m, int n)
{
    // If either given row number is first or given column
    // number is first
    if (m == 1 || n == 1)
        return 1;
 
    // If diagonal movements are allowed then the last
    // addition is required.
    return numberOfPaths(m - 1, n)
           + numberOfPaths(m, n - 1);
    // + numberOfPaths(m-1, n-1);
}
 
// Driver code
int main()
{
    cout << numberOfPaths(3, 3);
    return 0;
}

Java

// A Java program to count all possible paths
// from top left to bottom right
 
class GFG {
 
    // Returns count of possible paths to reach
    // cell at row number m and column number n
    // from the topmost leftmost cell (cell at 1, 1)
    static int numberOfPaths(int m, int n)
    {
        // If either given row number is first or
        // given column number is first
        if (m == 1 || n == 1)
            return 1;
 
        // If diagonal movements are allowed then
        // the last addition is required.
        return numberOfPaths(m - 1, n)
            + numberOfPaths(m, n - 1);
        // + numberOfPaths(m-1, n-1);
    }
 
      // Driver code
    public static void main(String args[])
    {
        System.out.println(numberOfPaths(3, 3));
    }
}
 
// This code is contributed by Sumit Ghosh

Python3

# Python program to count all possible paths
# from top left to bottom right
 
# function to return count of possible paths
# to reach cell at row number m and column
# number n from the topmost leftmost
# cell (cell at 1, 1)
 
 
def numberOfPaths(m, n):
    # If either given row number is first
    # or given column number is first
    if(m == 1 or n == 1):
        return 1
 
# If diagonal movements are allowed
# then the last addition
# is required.
    return numberOfPaths(m-1, n) + numberOfPaths(m, n-1)
 
 
# Driver program to test above function
if __name__ == '__main__':
  m = 3
  n = 3
  print(numberOfPaths(m, n))
 
# This code is contributed by Aditi Sharma

C#

// A C# program to count all possible paths
// from top left to bottom right
 
using System;
 
public class GFG {
    // Returns count of possible paths to reach
    // cell at row number m and column number n
    // from the topmost leftmost cell (cell at 1, 1)
    static int numberOfPaths(int m, int n)
    {
        // If either given row number is first or
        // given column number is first
        if (m == 1 || n == 1)
            return 1;
 
        // If diagonal movements are allowed then
        // the last addition is required.
        return numberOfPaths(m - 1, n)
            + numberOfPaths(m, n - 1);
        // + numberOfPaths(m-1, n-1);
    }
 
      // Driver code
    static public void Main()
    {
        Console.WriteLine(numberOfPaths(3, 3));
    }
}
 
// This code is contributed by ajit

Javascript

<script>
// A Javascript program to count all possible paths
// from top left to bottom right
     
    // Returns count of possible paths to reach
    // cell at row number m and column number n
    // from the topmost leftmost cell (cell at 1, 1)
    function numberOfPaths(m, n)
    {
     
        // If either given row number is first or
        // given column number is first
        if (m == 1 || n == 1)
            return 1;
         
        // If diagonal movements are allowed then
        // the last addition is required.
        return numberOfPaths(m - 1, n) + numberOfPaths(m, n - 1);
        
       // + numberOfPaths(m - 1, n - 1);
    }
     
    document.write(numberOfPaths(3, 3)+"<br>");
     
    // This code is contributed by rag2127
</script>

PHP

<?php
 
// Returns count of possible paths
// to reach cell at row number m
// and column number n from the
// topmost leftmost cell (cell at 1, 1)
function numberOfPaths($m, $n)
{
     
    // If either given row number
    // is first or given column
    // number is first
    if ($m == 1 || $n == 1)
            return 1;
     
    // If diagonal movements
    // are allowed then the last
    // addition is required.
    return numberOfPaths($m - 1, $n) +
           numberOfPaths($m, $n - 1);
}
 
// Driver Code
echo numberOfPaths(3, 3);
     
// This code is contributed by akt_mit
?>

Output

Time Complexity: O(2^N)
Auxiliary Space: O(N + M)

Count all possible paths from top left to the bottom right of a M X N matrix using Memoization:

To solve the problem follow the below idea:

As the above recursive solution has overlapping subproblems so we can declare a 2-D array to save the values for different states of the recursive function and later on use the values of this dp array to get the answer for already solved subproblems

Follow the below steps to solve the problem:

Declare a 2-D array of size N X M
Create a recursive function with parameters as row and column index and 2-D array
Call this recursive function for N-1 and M-1
In the recursive function
- If N == 1 or M == 1 then return 1
- If the value of this recursive function is not stored in the 2-D array then call the recursive function for (N-1, M, dp) and (N, M-1, dp) and assign the sum of answers of these functions in the 2-D array and return this value
- else return the value of this function stored in the 2-D array
Print the answer

Below is the implementation of the above approach:

C++

// A C++ program to count all possible paths from
// top left to top bottom right using
// Recursive Dynamic Programming
#include <bits/stdc++.h>
using namespace std;
 
// Returns count of possible paths to reach
// cell at row number m and column number n from
// the topmost leftmost cell (cell at 1, 1)
int numberOfPaths(int n, int m, int DP[4][4])
{
 
    if (n == 1 || m == 1)
        return DP[n][m] = 1;
 
    // Add the element in the DP table
    // If it was not computed before
    if (DP[n][m] == 0)
        DP[n][m] = numberOfPaths(n - 1, m, DP)
                   + numberOfPaths(n, m - 1, DP);
 
    return DP[n][m];
}
 
// Driver code
int main()
{
    // Create an empty 2D table
    int DP[4][4] = { 0 };
    memset(DP, 0, sizeof(DP));
 
    cout << numberOfPaths(3, 3, DP);
 
    return 0;
}
// This code is contributed
// by Gatea David

Java

// Java program to count all possible paths from
// top left to top bottom right using
// Recursive Dynamic Programming
import java.util.*;
public class GFG {
 
    // Returns count of possible paths to reach
    // cell at row number m and column number n from
    // the topmost leftmost cell (cell at 1, 1)
    static int numberOfPaths(int n, int m, int DP[][])
    {
 
        if (n == 1 || m == 1)
            return DP[n][m] = 1;
 
        // Add the element in the DP table
        // If it was not computed before
        if (DP[n][m] == 0)
            DP[n][m] = numberOfPaths(n - 1, m, DP)
                       + numberOfPaths(n, m - 1, DP);
 
        return DP[n][m];
    }
 
    // Driver code
    public static void main(String args[])
    {
        // Create an empty 2D table
        int DP[][] = new int[4][4];
        for (int i = 0; i < 4; i++) {
            for (int j = 0; j < 4; j++) {
                DP[i][j] = 0;
            }
        }
 
        System.out.println(numberOfPaths(3, 3, DP));
    }
}
 
// This code is contributed
// by Samim Hossain Mondal.

Python3

# Python program to count all possible paths from
# top left to top bottom right using
# Recursive Dynamic Programming
 
# Returns count of possible paths to reach
# cell at row number m and column number n from
# the topmost leftmost cell (cell at 1, 1)
 
 
def numberOfPaths(n, m, DP):
 
    if (n == 1 or m == 1):
        DP[n][m] = 1
        return 1
 
    # Add the element in the DP table
    # If it was not computed before
    if (DP[n][m] == 0):
        DP[n][m] = numberOfPaths(n - 1, m, DP) + numberOfPaths(n, m - 1, DP)
 
    return DP[n][m]
 
 
# Driver code
if __name__ == '__main__':
 
    # Create an empty 2D table
    DP = [[0 for i in range(4)] for j in range(4)]
 
    print(numberOfPaths(3, 3, DP))
 
# This code is contributed by gauravrajput1

C#

// C# program to count all possible paths from
// top left to top bottom right using
// Recursive Dynamic Programming
using System;
class GFG {
 
    // Returns count of possible paths to reach
    // cell at row number m and column number n from
    // the topmost leftmost cell (cell at 1, 1)
    static int numberOfPaths(int n, int m, int[, ] DP)
    {
 
        if (n == 1 || m == 1)
            return DP[n, m] = 1;
 
        // Add the element in the DP table
        // If it was not computed before
        if (DP[n, m] == 0)
            DP[n, m] = numberOfPaths(n - 1, m, DP)
                       + numberOfPaths(n, m - 1, DP);
 
        return DP[n, m];
    }
 
    // Driver code
    public static void Main()
    {
        // Create an empty 2D table
        int[, ] DP = new int[4, 4];
        for (int i = 0; i < 4; i++) {
            for (int j = 0; j < 4; j++) {
                DP[i, j] = 0;
            }
        }
 
        Console.WriteLine(numberOfPaths(3, 3, DP));
    }
}
 
// This code is contributed
// by Samim Hossain Mondal.

Javascript

<script>
// Javascript program to count all possible paths from
// top left to top bottom right using
// Recursive Dynamic Programming
 
// Create an empty 2D table
let DP = new Array(4);
for(let i = 0; i < 4; i++) {
     
    DP[i] = new Array(4);
    for(let j = 0; j < 4; j++) {
        DP[i][j] = 0;
    }
}
 
// Returns count of possible paths to reach
// cell at row number m and column number n from
// the topmost leftmost cell (cell at 1, 1)
function numberOfPaths(n, m, DP){
 
    if(n == 1 || m == 1)
        return DP[n][m] = 1;
     
    // Add the element in the DP table
    // If it was not computed before
    if(DP[n][m] == 0)
        DP[n][m] = numberOfPaths(n - 1, m,DP) + numberOfPaths(n, m - 1,DP);
 
    return DP[n][m];
}
 
// Driver code
 
document.write(numberOfPaths(3, 3,DP));
 
// This code is contributed
// by Samim Hossain Mondal.
 
</script>

Output

Time Complexity: O(N * M)
Auxiliary Space: (N * M)

Count all possible paths from the top left to the bottom right of a M X N matrix using DP:

To solve the problem follow the below idea:

So this problem has both properties (see this and this) of a dynamic programming problem. Like other typical Dynamic Programming(DP) problems, recomputations of the same subproblems can be avoided by constructing a temporary array count[][] in a bottom-up manner using the above recursive formula

Follow the below steps to solve the problem:

Declare a 2-D array count of size M * N
Set value of count[i][0] equal to 1 for 0 <= i < M as the answer of subproblem with a single column is equal to 1
Set value of count[0][j] equal to 1 for 0 <= j < N as the answer of subproblem with a single row is equal to 1
Create a nested for loop for 0 <= i < M and 0 <= j < N and assign count[i][j] equal to count[i-1][j] + count[i][j-1]
Print value of count[M-1][N-1]

Below is the implementation of the above approach:

C++

// A C++ program to count all possible paths
// from top left to bottom right
#include <bits/stdc++.h>
using namespace std;
 
// Returns count of possible paths to reach cell at
// row number m and column  number n from the topmost
// leftmost cell (cell at 1, 1)
int numberOfPaths(int m, int n)
{
    // Create a 2D table to store results of subproblems
    int count[m][n];
 
    // Count of paths to reach any cell in first column is 1
    for (int i = 0; i < m; i++)
        count[i][0] = 1;
 
    // Count of paths to reach any cell in first row is 1
    for (int j = 0; j < n; j++)
        count[0][j] = 1;
 
    // Calculate count of paths for other cells in
    // bottom-up manner using the recursive solution
    for (int i = 1; i < m; i++) {
        for (int j = 1; j < n; j++)
 
            // By uncommenting the last part the code
            // calculates the total possible paths if the
            // diagonal Movements are allowed
            count[i][j]
                = count[i - 1][j]
                  + count[i][j - 1]; //+ count[i-1][j-1];
    }
    return count[m - 1][n - 1];
}
 
// Driver code
int main()
{
    cout << numberOfPaths(3, 3);
    return 0;
}

Java

// A Java program to count all possible paths
// from top left to bottom right
 
import java.io.*;
 
class GFG {
    // Returns count of possible paths to reach
    // cell at row number m and column number n from
    // the topmost leftmost cell (cell at 1, 1)
    static int numberOfPaths(int m, int n)
    {
        // Create a 2D table to store results
        // of subproblems
        int count[][] = new int[m][n];
 
        // Count of paths to reach any cell in
        // first column is 1
        for (int i = 0; i < m; i++)
            count[i][0] = 1;
 
        // Count of paths to reach any cell in
        // first row is 1
        for (int j = 0; j < n; j++)
            count[0][j] = 1;
 
        // Calculate count of paths for other
        // cells in bottom-up manner using
        // the recursive solution
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++)
 
                // By uncommenting the last part the
                // code calculates the total possible paths
                // if the diagonal Movements are allowed
                count[i][j]
                    = count[i - 1][j]
                      + count[i]
                             [j - 1]; //+ count[i-1][j-1];
        }
        return count[m - 1][n - 1];
    }
 
    // Driver code
    public static void main(String args[])
    {
        System.out.println(numberOfPaths(3, 3));
    }
}
 
// This code is contributed by Sumit Ghosh

Python3

# Python3 program to count all possible paths
# from top left to bottom right
 
# Returns count of possible paths to reach cell
# at row number m and column number n from the
# topmost leftmost cell (cell at 1, 1)
 
 
def numberOfPaths(m, n):
    # Create a 2D table to store
    # results of subproblems
    # one-liner logic to take input for rows and columns
    # mat = [[int(input()) for x in range (C)] for y in range(R)]
 
    count = [[0 for x in range(n)] for y in range(m)]
 
    # Count of paths to reach any
    # cell in first column is 1
    for i in range(m):
        count[i][0] = 1
 
    # Count of paths to reach any
    # cell in first row is 1
    for j in range(n):
        count[0][j] = 1
 
    # Calculate count of paths for other
    # cells in bottom-up
    # manner using the recursive solution
    for i in range(1, m):
        for j in range(1, n):
            count[i][j] = count[i-1][j] + count[i][j-1]
    return count[m-1][n-1]
 
 
# Driver code
if __name__ == '__main__':
  m = 3
  n = 3
  print(numberOfPaths(m, n))
 
# This code is contributed by Aditi Sharma

C#

// A C#  program to count all possible paths
// from top left to bottom right
using System;
 
public class GFG {
 
    // Returns count of possible paths to reach
    // cell at row number m and column number n from
    // the topmost leftmost cell (cell at 1, 1)
    static int numberOfPaths(int m, int n)
    {
        // Create a 2D table to store results
        // of subproblems
        int[, ] count = new int[m, n];
 
        // Count of paths to reach any cell in
        // first column is 1
        for (int i = 0; i < m; i++)
            count[i, 0] = 1;
 
        // Count of paths to reach any cell in
        // first row is 1
        for (int j = 0; j < n; j++)
            count[0, j] = 1;
 
        // Calculate count of paths for other
        // cells in bottom-up manner using
        // the recursive solution
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++)
 
                // By uncommenting the last part the
                // code calculates the total possible paths
                // if the diagonal Movements are allowed
                count[i, j]
                    = count[i - 1, j]
                      + count[i,
                              j - 1]; //+ count[i-1][j-1];
        }
        return count[m - 1, n - 1];
    }
 
    // Driver code
    static public void Main()
    {
        Console.WriteLine(numberOfPaths(3, 3));
    }
}
 
// This code is contributed by akt_mit

Javascript

<script>
 
// A javascript program to count all possible paths
// from top left to bottom right
 
// Returns count of possible paths to reach
// cell at row number m and column number n from
// the topmost leftmost cell (cell at 1, 1)
function numberOfPaths(m , n)
{
    // Create a 2D table to store results
    // of subproblems
    var count = Array(m).fill(0).map(x => Array(n).fill(0));
 
    // Count of paths to reach any cell in
    // first column is 1
    for (i = 0; i < m; i++)
        count[i][0] = 1;
 
    // Count of paths to reach any cell in
    // first row is 1
    for (j = 0; j < n; j++)
        count[0][j] = 1;
 
    // Calculate count of paths for other
    // cells in bottom-up manner using
    // the recursive solution
    for (i = 1; i < m; i++) {
        for (j = 1; j < n; j++)
 
            // By uncommenting the last part the
            // code calculates the total possible paths
            // if the diagonal Movements are allowed
             
            //+ count[i-1][j-1];
            count[i][j] = count[i - 1][j] + count[i][j - 1];
    }
    return count[m - 1][n - 1];
}
 
// Driver program to test above function
document.write(numberOfPaths(3, 3));
 
// This code is contributed by 29AjayKumar
 
</script>

PHP

<?php
// A PHP program to count all possible
// paths from top left to bottom right
 
// Returns count of possible paths to
// reach cell at row number m and column
// number n from the topmost leftmost
// cell (cell at 1, 1)
function numberOfPaths($m, $n)
{
    // Create a 2D table to store
    // results of subproblems
    $count = array();
 
    // Count of paths to reach any cell
    // in first column is 1
    for ($i = 0; $i < $m; $i++)
        $count[$i][0] = 1;
 
    // Count of paths to reach any cell
    // in first row is 1
    for ($j = 0; $j < $n; $j++)
        $count[0][$j] = 1;
 
    // Calculate count of paths for other
    // cells in bottom-up manner using the
    // recursive solution
    for ($i = 1; $i < $m; $i++)
    {
        for ($j = 1; $j < $n; $j++)
 
            // By uncommenting the last part the
            // code calculated the total possible
            // paths if the diagonal Movements are allowed
            $count[$i][$j] = $count[$i - 1][$j] +
                             $count[$i][$j - 1]; //+ count[i-1][j-1];
    }
    return $count[$m - 1][$n - 1];
}
 
// Driver Code
echo numberOfPaths(3, 3);
 
// This code is contributed
// by Mukul Singh
?>

Output

Time Complexity: O(M * N) – Due to nested for loops.
Auxiliary Space: O(M * N) – We have used a 2D array of size M x N

Space optimization of the above approach:

To solve the problem follow the below idea:

We can space optimize the above dp approach as for calculating the values of the current row we require only previous row

Follow the below steps to solve the problem:

Declare an array dp of size N
Set dp[0] = 1
Create a nested for loop for 0 <= i < M and 0 <= j < N and add dp[j-1] to dp[j]
Print value of dp[n – 1]

Below is the implementation of the above approach:

C++

// C++ program for the above approach
 
#include <bits/stdc++.h>
using namespace std;
 
// Returns count of possible paths to reach
// cell at row number m and column number n from
// the topmost leftmost cell (cell at 1, 1)
int numberOfPaths(int m, int n)
{
    // Create a 1D array to store results of subproblems
    int dp[n] = { 1 };
    dp[0] = 1;
 
    for (int i = 0; i < m; i++) {
        for (int j = 1; j < n; j++) {
            dp[j] += dp[j - 1];
        }
    }
 
    return dp[n - 1];
}
 
// Driver code
int main() { cout << numberOfPaths(3, 3); }
 
// This code is contributed by mohit kumar 29

Java

// Java program for the above approach
import java.io.*;
 
class GFG {
    // Returns count of possible paths to reach
    // cell at row number m and column number n from
    // the topmost leftmost cell (cell at 1, 1)
    static int numberOfPaths(int m, int n)
    {
        // Create a 1D array to store results of subproblems
        int[] dp = new int[n];
        dp[0] = 1;
 
        for (int i = 0; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[j] += dp[j - 1];
            }
        }
 
        return dp[n - 1];
    }
 
    // Driver code
    public static void main(String args[])
    {
        System.out.println(numberOfPaths(3, 3));
    }
}

Python3

# Returns count of possible paths
# to reach cell at row number m and
# column number n from the topmost
# leftmost cell (cell at 1, 1)
 
 
def numberOfPaths(p, q):
 
    # Create a 1D array to store
    # results of subproblems
    dp = [1 for i in range(q)]
    for i in range(p - 1):
        for j in range(1, q):
            dp[j] += dp[j - 1]
    return dp[q - 1]
 
 
# Driver Code
if __name__ == '__main__':
  print(numberOfPaths(3, 3))
 
# This code is contributed
# by Ankit Yadav

C#

using System;
 
class GFG {
    // Returns count of possible paths
    // to reach cell at row number m
    // and column number n from the
    // topmost leftmost cell (cell at 1, 1)
    static int numberOfPaths(int m, int n)
    {
        // Create a 1D array to store
        // results of subproblems
        int[] dp = new int[n];
        dp[0] = 1;
 
        for (int i = 0; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[j] += dp[j - 1];
            }
        }
 
        return dp[n - 1];
    }
 
    // Driver Code
    public static void Main()
    {
        Console.Write(numberOfPaths(3, 3));
    }
}
 
// This code is contributed
// by ChitraNayal

Javascript

<script>
 
// Returns count of possible paths to reach
// cell at row number m and column number n from
// the topmost leftmost cell (cell at 1, 1)
function numberOfPaths(m , n)
{
    // Create a 1D array to store results of subproblems
    dp = Array.from({length: n}, (_, i) => 0);
    dp[0] = 1;
 
    for (i = 0; i < m; i++) {
        for (j = 1; j < n; j++) {
            dp[j] += dp[j - 1];
        }
    }
 
    return dp[n - 1];
}
 
// Driver program to test above function
document.write(numberOfPaths(3, 3));
 
// This code contributed by Princi Singh
 
</script>

PHP

<?php
// Returns count of possible paths to
// reach cell at row number m and
// column number n from the topmost
// leftmost cell (cell at 1, 1)
function numberOfPaths($m, $n)
{
    // Create a 1D array to store
    // results of subproblems
    $dp = array();
    $dp[0] = 1;
 
    for ($i = 0; $i < $m; $i++)
    {
    for ($j = 1; $j < $n; $j++)
    {
        $dp[$j] += $dp[$j - 1];
    }
    }
 
    return $dp[$n - 1];
}
 
// Driver Code
echo numberOfPaths(3, 3);
 
// This code is contributed
// by Akanksha Rai
?>

Output

Time Complexity: O(M * N), The program uses nested loops to fill the 1D array “dp”. The outer loop runs “m” times, and the inner loop runs “n-1” times. Therefore, the time complexity of the program is O(M*N).
Auxiliary Space: O(N), The program uses a 1D array “dp” of size “n” to store the results of subproblems. Hence, the space complexity of the program is O(N).

This code is contributed by Vivek Singh

Note: the count can also be calculated using the formula (M-1 + N-1)!/(M-1)! * (N-1)!

Count all possible paths from top left to the bottom right of a M X N matrix using combinatorics:

To solve the problem follow the below idea:

In this approach, We have to calculate ^m+n-2C_n-1here which will be (m+n-2)! / (n-1)! (m-1)!
m = number of rows, n = number of columns
Total number of moves in which we have to move down to reach the last row = m – 1 (m rows, since we are starting from (1, 1) that is not included)
Total number of moves in which we have to move right to reach the last column = n – 1 (n column, since we are starting from (1, 1) that is not included)
Down moves = (m – 1)
Right moves = (n – 1)
Total moves = Down moves + Right moves = (m – 1) + (n – 1)
Now think of moves as a string of ‘R’ and ‘D’ characters where ‘R’ at any ith index will tell us to move ‘Right’ and ‘D’ will tell us to move ‘Down’. Now think of how many unique strings (moves) we can make where in total there should be (n – 1 + m – 1) characters and there should be (m – 1) ‘D’ character and (n – 1) ‘R’ character?
Choosing positions of (n – 1) ‘R’ characters results in the automatic choosing of (m – 1) ‘D’ character positions
The number of ways to choose positions for (n – 1) ‘R’ character = ^{Total positions}C _{n – 1}= ^{Total positions}C _{m – 1} = (n – 1 + m – 1) != 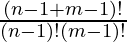$\frac {(n - 1 + m - 1)!} {(n - 1) ! (m - 1)!}$
Another way to think about this problem:
Count the Number of ways to make an N digit Binary String (String with 0s and 1s only) with ‘X’ zeros and ‘Y’ ones (here we have replaced ‘R’ with ‘0’ or ‘1’ and ‘D’ with ‘1’ or ‘0’ respectively whichever suits you better)

Follow the below steps to solve the problem:

Declare a variable path equal to 1
Create a for loop from i equal to n to (m + n – 1)
- Set path equal to path * i
- Set path equal to path divided by (i – n + 1)
Return path

Below is the implementation of the above approach:

C++

// A C++ program to count all possible paths from
// top left to top bottom using combinatorics
 
#include <bits/stdc++.h>
using namespace std;
 
int numberOfPaths(int m, int n)
{
    // We have to calculate m+n-2 C n-1 here
    // which will be (m+n-2)! / (n-1)! (m-1)!
    int path = 1;
    for (int i = n; i < (m + n - 1); i++) {
        path *= i;
        path /= (i - n + 1);
    }
    return path;
}
 
// Driver code
int main()
{
    cout << numberOfPaths(3, 3);
    return 0;
}
 
// This code is suggested by Kartik Sapra

Java

// Java program to count all possible paths from
// top left to top bottom using combinatorics
 
import java.io.*;
 
class GFG {
 
    static int numberOfPaths(int m, int n)
    {
        // We have to calculate m+n-2 C n-1 here
        // which will be (m+n-2)! / (n-1)! (m-1)!
        int path = 1;
        for (int i = n; i < (m + n - 1); i++) {
            path *= i;
            path /= (i - n + 1);
        }
        return path;
    }
 
    // Driver code
    public static void main(String[] args)
    {
        System.out.println(numberOfPaths(3, 3));
    }
}
 
// This code is contributed by Code_Mech.

Python3

# Python3 program to count all possible
# paths from top left to top bottom
# using combinatorics
 
 
def numberOfPaths(m, n):
    path = 1
    # We have to calculate m + n-2 C n-1 here
    # which will be (m + n-2)! / (n-1)! (m-1)! path = 1;
    for i in range(n, (m + n - 1)):
        path *= i
        path //= (i - n + 1)
 
    return path
 
 
# Driver code
print(numberOfPaths(3, 3))
 
# This code is contributed
# by Akanksha Rai

C#

// C# program to count all possible paths from
// top left to top bottom using combinatorics
using System;
 
class GFG {
 
    static int numberOfPaths(int m, int n)
    {
        // We have to calculate m+n-2 C n-1 here
        // which will be (m+n-2)! / (n-1)! (m-1)!
        int path = 1;
        for (int i = n; i < (m + n - 1); i++) {
            path *= i;
            path /= (i - n + 1);
        }
        return path;
    }
 
    // Driver code
    public static void Main()
    {
        Console.WriteLine(numberOfPaths(3, 3));
    }
}
 
// This code is contributed by Code_Mech.

Javascript

<script>
 
// javascript program to count all possible paths from
// top left to top bottom using combinatorics  
function numberOfPaths(m , n)
    {
        // We have to calculate m+n-2 C n-1 here
        // which will be (m+n-2)! / (n-1)! (m-1)!
        var path = 1;
        for (i = n; i < (m + n - 1); i++) {
            path *= i;
            path = parseInt(path/(i - n + 1));
        }
        return path;
    }
 
// Driver code
document.write(numberOfPaths(3, 3));
 
// This code contributed by Princi Singh
</script>

PHP

<?php
 
// PHP program to count all possible paths from
// top left to top bottom using combinatorics
function numberOfPaths($m, $n)
{
    // We have to calculate m+n-2 C n-1 here
    // which will be (m+n-2)! / (n-1)! (m-1)!
    $path = 1;
    for ($i = $n; $i < ($m + $n - 1); $i++)
    {
        $path *= $i;
        $path /= ($i - $n + 1);
    }
    return $path;
}
 
// Driver code
{
    echo(numberOfPaths(3, 3));
}
 
// This code is contributed by Code_Mech.

Output

Time Complexity: O(M), The time complexity is O(M), where M is the maximum of m and n. This is because the for loop iterates M times, and each iteration involves a constant number of arithmetic operations.
Auxiliary Space: O(1), The space complexity of the program is also O(1), which means that it uses a constant amount of memory regardless of the input size. This is because the program does not create any data structures or arrays that grow with the input size, and all calculations are done using only a few variables.

This article is contributed by Hariprasad NG. Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.

Last Updated : 21 Sep, 2023