Printing Items in 0/1 Knapsack

Given weights and values of n items, put these items in a knapsack of capacity W to get the maximum total value in the knapsack. In other words, given two integer arrays, val[0..n-1] and wt[0..n-1] represent values and weights associated with n items respectively. Also given an integer W which represents knapsack capacity, find out the items such that sum of the weights of those items of a given subset is smaller than or equal to W. You cannot break an item, either pick the complete item or don’t pick it (0-1 property).
Prerequisite : 0/1 Knapsack
Examples :

Input : val[] = {60, 100, 120};
        wt[] = {10, 20, 30};
        W = 50;
Output : 220 //maximum value that can be obtained
         30 20 //weights 20 and 30 are included. 

Input : val[] = {40, 100, 50, 60};
        wt[] = {20, 10, 40, 30};
        W = 60;
Output : 200
         30 20 10

Approach :
Let val[] = {1, 4, 5, 7}, wt[] = {1, 3, 4, 5} 
W = 7. 
The 2d knapsack table will look like : 

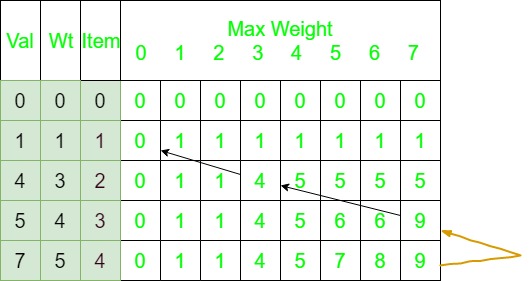
Start backtracking from K[n][W].Here K[n][W] is 9.
Since this value comes from the top (shown by grey arrow), the item in this row is not included. Go vertically upward in the table without including this in the knapsack. Now, this value K[n-1][W] which is 9 doesn’t come from the top which means the item in this row is included and go vertically up and then left by the weight of the included item ( shown by black arrow). Continuing this process include weights 3 and 4 with a total value 9 in the knapsack. 

C++

// CPP code for Dynamic Programming based
// solution for 0-1 Knapsack problem
#include <bits/stdc++.h>
#include <iostream>
using namespace std;

// A utility function that returns maximum of two integers
int max(int a, int b) { return (a > b) ? a : b; }

// Prints the items which are put in a knapsack of capacity W
void printknapSack(int W, int wt[], int val[], int n)
{
    int i, w;
    int K[n + 1][W + 1];

    // Build table K[][] in bottom up manner
    for (i = 0; i <= n; i++) {
        for (w = 0; w <= W; w++) {
            if (i == 0 || w == 0)
                K[i][w] = 0;
            else if (wt[i - 1] <= w)
                K[i][w] = max(val[i - 1] +
                    K[i - 1][w - wt[i - 1]], K[i - 1][w]);
            else
                K[i][w] = K[i - 1][w];
        }
    }

    // stores the result of Knapsack
    int res = K[n][W];
    cout<< res << endl;

    w = W;
    for (i = n; i > 0 && res > 0; i--) {

        // either the result comes from the top
        // (K[i-1][w]) or from (val[i-1] + K[i-1]
        // [w-wt[i-1]]) as in Knapsack table. If
        // it comes from the latter one/ it means
        // the item is included.
        if (res == K[i - 1][w])
            continue;
        else {

            // This item is included.
            cout<<" "<<wt[i - 1] ;

            // Since this weight is included its
            // value is deducted
            res = res - val[i - 1];
            w = w - wt[i - 1];
        }
    }
}

// Driver code
int main()
{
    int val[] = { 60, 100, 120 };
    int wt[] = { 10, 20, 30 };
    int W = 50;
    int n = sizeof(val) / sizeof(val[0]);

    printknapSack(W, wt, val, n);

    return 0;
}

// this code is contributed by shivanisinghss2110

C

// CPP code for Dynamic Programming based
// solution for 0-1 Knapsack problem
#include <stdio.h>

// A utility function that returns maximum of two integers
int max(int a, int b) { return (a > b) ? a : b; }

// Prints the items which are put in a knapsack of capacity W
void printknapSack(int W, int wt[], int val[], int n)
{
    int i, w;
    int K[n + 1][W + 1];

    // Build table K[][] in bottom up manner
    for (i = 0; i <= n; i++) {
        for (w = 0; w <= W; w++) {
            if (i == 0 || w == 0)
                K[i][w] = 0;
            else if (wt[i - 1] <= w)
                K[i][w] = max(val[i - 1] +
                    K[i - 1][w - wt[i - 1]], K[i - 1][w]);
            else
                K[i][w] = K[i - 1][w];
        }
    }

    // stores the result of Knapsack
    int res = K[n][W];
    printf("%d\n", res);

    w = W;
    for (i = n; i > 0 && res > 0; i--) {

        // either the result comes from the top
        // (K[i-1][w]) or from (val[i-1] + K[i-1]
        // [w-wt[i-1]]) as in Knapsack table. If
        // it comes from the latter one/ it means
        // the item is included.
        if (res == K[i - 1][w])
            continue;
        else {

            // This item is included.
            printf("%d ", wt[i - 1]);

            // Since this weight is included its
            // value is deducted
            res = res - val[i - 1];
            w = w - wt[i - 1];
        }
    }
}

// Driver code
int main()
{
    int val[] = { 60, 100, 120 };
    int wt[] = { 10, 20, 30 };
    int W = 50;
    int n = sizeof(val) / sizeof(val[0]);

    printknapSack(W, wt, val, n);

    return 0;
}

Java

// Java code for Dynamic Programming based
// solution for 0-1 Knapsack problem

class GFG {

    // A utility function that returns
    // maximum of two integers
    static int max(int a, int b)
    {
        return (a > b) ? a : b;
    }

    // Prints the items which are put
    // in a knapsack of capacity W
    static void printknapSack(int W, int wt[],
                             int val[], int n)
    {
        int i, w;
        int K[][] = new int[n + 1][W + 1];

        // Build table K[][] in bottom up manner
        for (i = 0; i <= n; i++) {
            for (w = 0; w <= W; w++) {
                if (i == 0 || w == 0)
                    K[i][w] = 0;
                else if (wt[i - 1] <= w)
                    K[i][w] = Math.max(val[i - 1] +
                              K[i - 1][w - wt[i - 1]], K[i - 1][w]);
                else
                    K[i][w] = K[i - 1][w];
            }
        }

        // stores the result of Knapsack
        int res = K[n][W];
        System.out.println(res);

        w = W;
        for (i = n; i > 0 && res > 0; i--) {

            // either the result comes from the top
            // (K[i-1][w]) or from (val[i-1] + K[i-1]
            // [w-wt[i-1]]) as in Knapsack table. If
            // it comes from the latter one/ it means
            // the item is included.
            if (res == K[i - 1][w])
                continue;
            else {

                // This item is included.
                System.out.print(wt[i - 1] + " ");

                // Since this weight is included its
                // value is deducted
                res = res - val[i - 1];
                w = w - wt[i - 1];
            }
        }
    }

    // Driver code
    public static void main(String arg[])
    {
        int val[] = { 60, 100, 120 };
        int wt[] = { 10, 20, 30 };
        int W = 50;
        int n = val.length;

        printknapSack(W, wt, val, n);
    }
}

// This code is contributed by Anant Agarwal.

Python3

# Python3 code for Dynamic Programming
# based solution for 0-1 Knapsack problem

# Prints the items which are put in a
# knapsack of capacity W
def printknapSack(W, wt, val, n):
    K = [[0 for w in range(W + 1)]
            for i in range(n + 1)]

    # Build table K[][] in bottom
    # up manner
    for i in range(n + 1):
        for w in range(W + 1):
            if i == 0 or w == 0:
                K[i][w] = 0
            elif wt[i - 1] <= w:
                K[i][w] = max(val[i - 1]
                  + K[i - 1][w - wt[i - 1]],
                               K[i - 1][w])
            else:
                K[i][w] = K[i - 1][w]

    # stores the result of Knapsack
    res = K[n][W]
    print(res)

    w = W
    for i in range(n, 0, -1):
        if res <= 0:
            break
        # either the result comes from the
        # top (K[i-1][w]) or from (val[i-1]
        # + K[i-1] [w-wt[i-1]]) as in Knapsack
        # table. If it comes from the latter
        # one/ it means the item is included.
        if res == K[i - 1][w]:
            continue
        else:

            # This item is included.
            print(wt[i - 1])

            # Since this weight is included
            # its value is deducted
            res = res - val[i - 1]
            w = w - wt[i - 1]

# Driver code
val = [ 60, 100, 120 ]
wt = [ 10, 20, 30 ]
W = 50
n = len(val)

printknapSack(W, wt, val, n)

# This code is contributed by Aryan Garg.

C#

// C# code for Dynamic Programming based
// solution for 0-1 Knapsack problem

using System ;

class GFG {

    // A utility function that returns
    // maximum of two integers
    static int max(int a, int b)
    {
        return (a > b) ? a : b;
    }

    // Prints the items which are put
    // in a knapsack of capacity W
    static void printknapSack(int W, int []wt,
                            int []val, int n)
    {
        int i, w;
        int [,]K = new int[n + 1,W + 1];

        // Build table K[][] in bottom up manner
        for (i = 0; i <= n; i++) {
            for (w = 0; w <= W; w++) {
                if (i == 0 || w == 0)
                    K[i,w] = 0;
                else if (wt[i - 1] <= w)
                    K[i,w] = Math.Max(val[i - 1] +
                            K[i - 1,w - wt[i - 1]], K[i - 1,w]);
                else
                    K[i,w] = K[i - 1,w];
            }
        }

        // stores the result of Knapsack
        int res = K[n,W];
        Console.WriteLine(res);

        w = W;
        for (i = n; i > 0 && res > 0; i--) {

            // either the result comes from the top
            // (K[i-1][w]) or from (val[i-1] + K[i-1]
            // [w-wt[i-1]]) as in Knapsack table. If
            // it comes from the latter one/ it means
            // the item is included.
            if (res == K[i - 1,w])
                continue;
            else {

                // This item is included.
                Console.Write(wt[i - 1] + " ");

                // Since this weight is included its
                // value is deducted
                res = res - val[i - 1];
                w = w - wt[i - 1];
            }
        }
    }

    // Driver code
    public static void Main()
    {
        int []val = { 60, 100, 120 };
        int []wt = { 10, 20, 30 };
        int W = 50;
        int n = val.Length;

        printknapSack(W, wt, val, n);
    }
}

// This code is contributed by Ryuga.

PHP

<?php
// PHP code for Dynamic Programming based
// solution for 0-1 Knapsack problem

// Prints the items which are kept in
// a knapsack of capacity W
function printknapSack($W, &$wt, &$val, $n)
{
    $K = array_fill(0, $n + 1,
         array_fill(0, $W + 1, NULL));

    // Build table K[][] in bottom up manner
    for ($i = 0; $i <= $n; $i++)
    {
        for ($w = 0; $w <= $W; $w++)
        {
            if ($i == 0 || $w == 0)
                $K[$i][$w] = 0;
            else if ($wt[$i - 1] <= $w)
                $K[$i][$w] = max($val[$i - 1] +
                    $K[$i - 1][$w - $wt[$i - 1]],
                                 $K[$i - 1][$w]);
            else
                $K[$i][$w] = $K[$i - 1][$w];
        }
    }

    // stores the result of Knapsack
    $res = $K[$n][$W];
    echo $res . "\n";

    $w = $W;
    for ($i = $n; $i > 0 && $res > 0; $i--)
    {

        // either the result comes from the top
        // (K[i-1][w]) or from (val[i-1] + K[i-1]
        // [w-wt[i-1]]) as in Knapsack table. If
        // it comes from the latter one/ it means
        // the item is included.
        if ($res == $K[$i - 1][$w])
            continue;
        else
        {

            // This item is included.
            echo $wt[$i - 1] . " ";

            // Since this weight is included
            // its value is deducted
            $res = $res - $val[$i - 1];
            $w = $w - $wt[$i - 1];
        }
    }
}

// Driver code
$val = array(60, 100, 120);
$wt = array(10, 20, 30);
$W = 50;
$n = sizeof($val);
printknapSack($W, $wt, $val, $n);

// This code is contributed by ita_c
?>

Javascript

<script>

// JavaScript code for Dynamic Programming based
// solution for 0-1 Knapsack problem

    // A utility function that returns
    // maximum of two integers
    function max(a,b)
    {
        return (a > b) ? a : b;
    }


    // Prints the items which are put
    // in a knapsack of capacity W
    function printknapSack(W,wt,val,n)
    {
        let i, w;
        let K = new Array(n + 1);
        for( i=0;i<K.length;i++)
        {
            K[i]=new Array(W+1);
            for(let j=0;j<W+1;j++)
            {
                K[i][j]=0;
            }
        }

        // Build table K[][] in bottom up manner
        for (i = 0; i <= n; i++) {
            for (w = 0; w <= W; w++) {
                if (i == 0 || w == 0)
                    K[i][w] = 0;
                else if (wt[i - 1] <= w)
                    K[i][w] = Math.max(val[i - 1] +
                        K[i - 1][w - wt[i - 1]],
                        K[i - 1][w]);
                else
                    K[i][w] = K[i - 1][w];
            }
        }

        // stores the result of Knapsack
        let res = K[n][W];
        document.write(res+"<br>");

        w = W;
        for (i = n; i > 0 && res > 0; i--)
        {

            // either the result comes from the top
            // (K[i-1][w]) or from (val[i-1] + K[i-1]
            // [w-wt[i-1]]) as in Knapsack table. If
            // it comes from the latter one/ it means
            // the item is included.
            if (res == K[i - 1][w])
                continue;
            else {

                // This item is included.
                document.write(wt[i - 1] + " ");

                // Since this weight is included its
                // value is deducted
                res = res - val[i - 1];
                w = w - wt[i - 1];
            }
        }
    }

    let val=[60, 100, 120 ];
    let wt=[10, 20, 30 ];
    let  W = 50;
    let n = val.length;
    printknapSack(W, wt, val, n);

    // This code is contributed by avanitrachhadiya2155

</script>

Output:

220
30 20

Time complexity: O(n*W)

Space complexity: O(n*W)