Overlapping Subproblems Property in Dynamic Programming | DP-1

Dynamic Programming is an algorithmic paradigm that solves a given complex problem by breaking it into subproblems using recursion and storing the results of subproblems to avoid computing the same results again. Following are the two main properties of a problem that suggests that the given problem can be solved using Dynamic programming.

• Overlapping Subproblems 
• Optimal Substructure

In this post, we will discuss the first property Overlapping Subproblems in detail. The second property of Dynamic programming is discussed in the next post.

Overlapping Subproblems:

Like Divide and Conquer, Dynamic Programming combines solutions to sub-problems. Dynamic Programming is mainly used when solutions to the same subproblems are needed again and again. In dynamic programming, computed solutions to subproblems are stored in a table so that these don’t have to be recomputed. So Dynamic Programming is not useful when there are no common (overlapping) subproblems because there is no point in storing the solutions if they are not needed again. For example, Binary Search doesn’t have common subproblems. If we take the example of following a recursive program for Fibonacci Numbers, there are many subproblems that are solved again and again.

C++

#include <iostream>
using namespace std;

/* a simple recursive program for Fibonacci numbers */
int fib(int n)
{
    if (n <= 1)
        return n;

    return fib(n - 1) + fib(n - 2);
}

int main() {

    cout << fib(7);

    return 0;
}

// This code is contributed by sanjoy_62.

C

/* a simple recursive program for Fibonacci numbers */
int fib(int n)
{
    if (n <= 1)
        return n;

    return fib(n - 1) + fib(n - 2);
}

Java

/*package whatever //do not write package name here */
/* a simple recursive program for Fibonacci numbers */
static int fib(int n)
{
    if (n <= 1)
        return n;

    return fib(n - 1) + fib(n - 2);
}

// This code is contributed by umadevi9616

Python

#  a simple recursive program for Fibonacci numbers
def fib(n):
    if n <= 1:
        return n

    return fib(n - 1) + fib(n - 2)

C#

/* a simple recursive program for Fibonacci numbers */
static int fib(int n)
{
    if (n <= 1)
        return n;

    return fib(n - 1) + fib(n - 2);
}


// This code contributed by umadevi9616

Javascript

<script>
/*package whatever //do not write package name here */
/* a simple recursive program for Fibonacci numbers */
function fib(n)
{
    if (n <= 1)
        return n;

    return fib(n - 1) + fib(n - 2);
}

// This code is contributed by gauravrajput1
</script>

Output

13

Time Complexity: O(2^N)  
Auxiliary Space: O(1)

Illustration of Recursion tree for the execution of fib(5) :

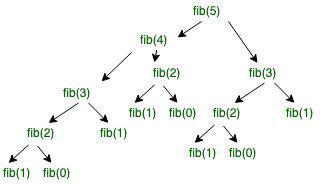
Recursion tree for the execution of fib(5) 

We can see that the function fib(3) is being called 2 times. If we would have stored the value of fib(3), then instead of computing it again, we could have reused the old stored value. There are following two different ways to store the values so that these values can be reused: 

• Memoization (Top Down) 
• Tabulation (Bottom Up)

Memoization (Top Down):

The memoized program for a problem is similar to the recursive version with a small modification that looks into a lookup table before computing solutions. We initialize a lookup array with all initial values as NIL. Whenever we need the solution to a subproblem, we first look into the lookup table. If the precomputed value is there then we return that value, otherwise, we calculate the value and put the result in the lookup table so that it can be reused later.

Following is the memoized version for the nth Fibonacci Number. 

C++

/* C++ program for Memoized version
for nth Fibonacci number */
#include <bits/stdc++.h>
using namespace std;
#define NIL -1
#define MAX 100

int lookup[MAX];

/* Function to initialize NIL
values in lookup table */
void _initialize()
{
    int i;
    for (i = 0; i < MAX; i++)
        lookup[i] = NIL;
}

/* function for nth Fibonacci number */
int fib(int n)
{
    if (lookup[n] == NIL) {
        if (n <= 1)
            lookup[n] = n;
        else
            lookup[n] = fib(n - 1) + fib(n - 2);
    }

    return lookup[n];
}

// Driver code
int main()
{
    int n = 40;
    _initialize();
    cout << "Fibonacci number is " << fib(n);
    return 0;
}

// This is code is contributed by rathbhupendra

C

/* C program for Memoized version for nth Fibonacci number
 */
#include <stdio.h>
#define NIL -1
#define MAX 100

int lookup[MAX];

/* Function to initialize NIL values in lookup table */
void _initialize()
{
    int i;
    for (i = 0; i < MAX; i++)
        lookup[i] = NIL;
}

/* function for nth Fibonacci number */
int fib(int n)
{
    if (lookup[n] == NIL) {
        if (n <= 1)
            lookup[n] = n;
        else
            lookup[n] = fib(n - 1) + fib(n - 2);
    }

    return lookup[n];
}

int main()
{
    int n = 40;
    _initialize();
    printf("Fibonacci number is %d ", fib(n));
    return 0;
}

Java

/* Java program for Memoized version */
public class Fibonacci {
    final int MAX = 100;
    final int NIL = -1;

    int lookup[] = new int[MAX];

    /* Function to initialize NIL values in lookup table */
    void _initialize()
    {
        for (int i = 0; i < MAX; i++)
            lookup[i] = NIL;
    }

    /* function for nth Fibonacci number */
    int fib(int n)
    {
        if (lookup[n] == NIL) {
            if (n <= 1)
                lookup[n] = n;
            else
                lookup[n] = fib(n - 1) + fib(n - 2);
        }
        return lookup[n];
    }

    public static void main(String[] args)
    {
        Fibonacci f = new Fibonacci();
        int n = 40;
        f._initialize();
        System.out.println("Fibonacci number is"
                           + " " + f.fib(n));
    }
}
// This Code is Contributed by Saket Kumar

Python

# a program for Memoized version of nth Fibonacci number

# function to calculate nth Fibonacci number


def fib(n, lookup):

    # base case
    if n <= 1:
        lookup[n] = n

    # if the value is not calculated previously then calculate it
    if lookup[n] is None:
        lookup[n] = fib(n-1, lookup) + fib(n-2, lookup)

    # return the value corresponding to that value of n
    return lookup[n]
# end of function

# Driver program to test the above function


def main():
    n = 34
    # Declaration of lookup table
    # Handles till n = 100
    lookup = [None] * 101
    print "Fibonacci Number is ", fib(n, lookup)


if __name__ == "__main__":
    main()

# This code is contributed by Nikhil Kumar Singh(nickzuck_007)

C#

// C# program for Memoized versionof nth Fibonacci number
using System;

class GFG {

    static int MAX = 100;
    static int NIL = -1;
    static int[] lookup = new int[MAX];

    /* Function to initialize NIL
    values in lookup table */
    static void initialize()
    {
        for (int i = 0; i < MAX; i++)
            lookup[i] = NIL;
    }

    /* function for nth Fibonacci number */
    static int fib(int n)
    {
        if (lookup[n] == NIL) {
            if (n <= 1)
                lookup[n] = n;
            else
                lookup[n] = fib(n - 1) + fib(n - 2);
        }
        return lookup[n];
    }

    // Driver code
    public static void Main()
    {

        int n = 40;
        initialize();
        Console.Write("Fibonacci number is"
                      + " " + fib(n));
    }
}

// This Code is Contributed by Sam007

Javascript

<script>

let  MAX = 100;
let NIL = -1;

let lookup = new Array(MAX);

function  _initialize()
{
    for (let i = 0; i < MAX; i++)
        lookup[i] = NIL;
}

function fib(n)
{
    if (lookup[n] == NIL)
    {
      if (n <= 1)
          lookup[n] = n;
      else
          lookup[n] = fib(n-1) + fib(n-2);
    }
    return lookup[n];
}


let n = 40;
_initialize();
document.write("Fibonacci number is" + " " + fib(n)+"<br>");

// This code is contributed by avanitrachhadiya2155
</script>

Output

Fibonacci number is 102334155

Time Complexity: O(N). This is because the algorithm computes each Fibonacci number only once and stores the result in an array for future use. Subsequent calls to the function with the same input value of n will retrieve the stored value from the lookup table, avoiding the need to recompute it. Therefore, the time complexity is linear, and the algorithm is very efficient for large values of n.

Space Complexity: O(N) as lookup table has been created.

Tabulation (Bottom Up):

The tabulated program for a given problem builds a table in a bottom-up fashion and returns the last entry from the table. For example, for the same Fibonacci number, we first calculate fib(0) then fib(1) then fib(2) then fib(3), and so on. So literally, we are building the solutions to subproblems bottom-up. 

Following is the tabulated version for the nth Fibonacci Number.

C

/* C program for Tabulated version */
#include <stdio.h>
int fib(int n)
{
    int f[n + 1];
    int i;
    f[0] = 0;
    f[1] = 1;
    for (i = 2; i <= n; i++)
        f[i] = f[i - 1] + f[i - 2];

    return f[n];
}

int main()
{
    int n = 9;
    printf("Fibonacci number is %d ", fib(n));
    return 0;
}

Java

/* Java program for Tabulated version */
public class Fibonacci {
    int fib(int n)
    {
        int f[] = new int[n + 1];
        f[0] = 0;
        f[1] = 1;
        for (int i = 2; i <= n; i++)
            f[i] = f[i - 1] + f[i - 2];
        return f[n];
    }

    public static void main(String[] args)
    {
        Fibonacci f = new Fibonacci();
        int n = 9;
        System.out.println("Fibonacci number is"
                           + " " + f.fib(n));
    }
}
// This Code is Contributed by Saket Kumar

Python

# Python program Tabulated (bottom up) version
def fib(n):

    # array declaration
    f = [0] * (n + 1)

    # base case assignment
    f[1] = 1

    # calculating the fibonacci and storing the values
    for i in xrange(2, n + 1):
        f[i] = f[i - 1] + f[i - 2]
    return f[n]

# Driver program to test the above function


def main():
    n = 9
    print "Fibonacci number is ", fib(n)


if __name__ == "__main__":
    main()

# This code is contributed by Nikhil Kumar Singh (nickzuck_007)

C#

// C# program for Tabulated version
using System;

class GFG {
    static int fib(int n)
    {
        int[] f = new int[n + 1];
        f[0] = 0;
        f[1] = 1;
        for (int i = 2; i <= n; i++)
            f[i] = f[i - 1] + f[i - 2];
        return f[n];
    }

    public static void Main()
    {

        int n = 9;
        Console.Write("Fibonacci number is"
                      + " " + fib(n));
    }
}

// This Code is Contributed by Sam007

Javascript

<script>

// Javascript program for Tabulated version
function fib(n)
{
    var f = new Array(n + 1);
    var i;

    f[0] = 0;
    f[1] = 1;
    for(i = 2; i <= n; i++)
        f[i] = f[i - 1] + f[i - 2];

    return f[n];
}

// Driver code
var n = 9;
document.write("Fibonacci number is  " + fib(n));

// This code is contributed by akshitsaxenaa09

</script>

PHP

<?php
// PHP program for Tabulated version

function fib($n)
{
    $f[$n + 1]=0;
    $i;
    $f[0] = 0;
    $f[1] = 1;
    for ($i = 2; $i <= $n; $i++)
        $f[$i] = $f[$i - 1] +
                 $f[$i - 2];

    return $f[$n];
}

// Driver Code
$n = 9;
echo("Fibonacci number is ");
echo(fib($n));

// This code is contributed by nitin mittal.
?>

C++

/* C++ program for Tabulated version */

#include <iostream>
using namespace std;

int fib(int n)
{
    int f[n + 1];
    int i;
    f[0] = 0;
    f[1] = 1;
    for (i = 2; i <= n; i++)
        f[i] = f[i - 1] + f[i - 2];

    return f[n];
}

int main()
{
    int n = 9;
    printf("Fibonacci number is %d ", fib(n));
    return 0;
}

Output

Fibonacci number is 34 

Time Complexity: O(N)
Auxiliary Space: O(N)