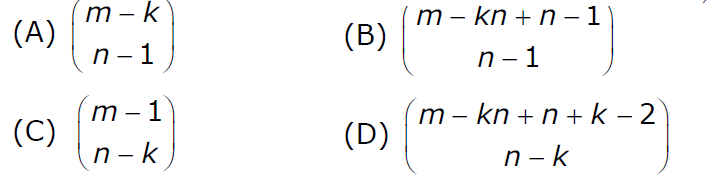Combinatorics
Question 1
How many onto (or surjective) functions are there from an n-element (n >= 2) set to a 2-element set?
Question 3
What is the maximum number of different Boolean functions involving n Boolean variables?
Question 4
Suppose that a robot is placed on the Cartesian plane. At each step it is allowed to move either one unit up or one unit right, i.e., if it is at (i,j) then it can move to either (i+1,j) or (i,j+1).
How many distinct paths are there for the robot to reach the point (10,10) starting from the initial position (0, 0)
Question 5
Question 7
Mala has a colouring book in which each English letter is drawn two times. She wants to paint each of these 52 prints with one of k colours, such that the colour-pairs used to colour any two letters are different. Both prints of a letter can also be coloured with the same colour. What is the minimum value of k that satisfies this requirement ?
Question 8
Let A be a sequence of 8 distinct integers sorted in ascending order. How many distinct pairs of sequences, B and C are there such that (i) each is sorted in ascending order, (ii) B has 5 and C has 3 elements, and (iii) the result of merging B and C gives A?
Question 9
Question 10
There are 22 questions to complete.