Cutting a Rod | DP-13
Last Updated :
13 Apr, 2024
Given a rod of length n inches and an array of prices that includes prices of all pieces of size smaller than n. Determine the maximum value obtainable by cutting up the rod and selling the pieces. For example, if the length of the rod is 8 and the values of different pieces are given as the following, then the maximum obtainable value is 22 (by cutting in two pieces of lengths 2 and 6)
length | 1 2 3 4 5 6 7 8
--------------------------------------------
price | 1 5 8 9 10 17 17 20
And if the prices are as follows, then the maximum obtainable value is 24 (by cutting in eight pieces of length 1)
length | 1 2 3 4 5 6 7 8
--------------------------------------------
price | 3 5 8 9 10 17 17 20
Method 1: A naive solution to this problem is to generate all configurations of different pieces and find the highest-priced configuration. This solution is exponential in terms of time complexity. Let us see how this problem possesses both important properties of a Dynamic Programming (DP) Problem and can efficiently be solved using Dynamic Programming.
1) Optimal Substructure:
We can get the best price by making a cut at different positions and comparing the values obtained after a cut. We can recursively call the same function for a piece obtained after a cut.
Let cutRod(n) be the required (best possible price) value for a rod of length n. cutRod(n) can be written as follows.
cutRod(n) = max(price[i] + cutRod(n-i-1)) for all i in {0, 1 .. n-1}
C++
// A recursive solution for Rod cutting problem
#include <bits/stdc++.h>
#include <iostream>
#include <math.h>
using namespace std;
// A utility function to get the maximum of two integers
int max(int a, int b) { return (a > b) ? a : b; }
/* Returns the best obtainable price for a rod of length n
and price[] as prices of different pieces */
int cutRod(int price[], int index, int n)
{
// base case
if (index == 0) {
return n * price[0];
}
// if n is 0 we cannot cut the rod anymore.
if (n ==0) {
return 0;}
//At any index we have 2 options either
//cut the rod of this length or not cut
//it
int notCut = cutRod(price,index - 1,n);
int cut = INT_MIN;
int rod_length = index + 1;
if (rod_length <= n)
cut = price[index]
+ cutRod(price,index,n - rod_length);
return max(notCut, cut);
}
/* Driver program to test above functions */
int main()
{
int arr[] = { 1, 5, 8, 9, 10, 17, 17, 20 };
int size = sizeof(arr) / sizeof(arr[0]);
cout << "Maximum Obtainable Value is "
<< cutRod(arr, size - 1, size);
getchar();
return 0;
}
//This code is contributed by Sanskar
// Java recursive solution for Rod cutting problem
import java.io.*;
class GFG {
/* Returns the best obtainable price for a rod of length
n and price[] as prices of different pieces */
static int cutRod(int price[], int index, int n)
{
// base case
// if index ==0 that means we can get n number of pieces of unit length with price price[0]
if (index == 0) {
return n * price[0];
}
// if n, the size of the rod is 0 we cannot cut the rod anymore.
if (n ==0) {
return 0;
}
// At any index we have 2 options either
// cut the rod of this length or not cut
// it
int notCut = cutRod(price, index - 1, n);
int cut = Integer.MIN_VALUE;
int rod_length = index + 1;
int new_length = n - rod_length;
// rod can be cut only if current rod length is than actual length of the rod
if (rod_length <= n)
//next cutting index can only be new length - 1
cut = price[index]
+ cutRod(price, new_length-1, new_length);
return Math.max(notCut, cut);
}
/* Driver program to test above functions */
public static void main(String args[])
{
int arr[] = { 1, 5, 8, 9, 10, 17, 17, 20};
int size = arr.length;
System.out.println("Maximum Obtainable Value is "
+ cutRod(arr, size - 1, size));
}
}
// This code is contributed by saikrishna padamatinti
// C# recursive solution for Rod cutting problem
using System;
public class GFG {
static int max(int a, int b) {
if (a > b) return a;
return b;
}
static int MIN_VALUE = -1000000000;
/* Returns the best obtainable price for a rod of
// length n and price[] as prices of different pieces */
static int cutRod(int[] price, int index, int n) {
// base case
if (index == 0) {
return n * price[0];
}
// if n is 0 we cannot cut the rod anymore.
if (n ==0) {
return 0;
}
// At any index we have 2 options either
// cut the rod of this length or not cut it
int notCut = cutRod(price, index - 1, n);
int cut = MIN_VALUE;
int rod_length = index + 1;
if (rod_length <= n)
cut = price[index] + cutRod(price, index, n - rod_length);
return max(notCut, cut);
}
// Driver program to test above functions
public static void Main(string[] args) {
int[] arr = {1, 5, 8, 9, 10, 17, 17, 20 };
int size = arr.Length;
Console.WriteLine("Maximum Obtainable Value is " +
cutRod(arr, size - 1, size));
}
}
// This code is contributed by ajaymakavana.
// A recursive solution for Rod cutting problem
/* Returns the best obtainable price for a rod of length n
and price[] as prices of different pieces */
function cutRod(price, index, n)
{
// base case
if (index == 0) {
return n * price[0];
}
// if n is 0 we cannot cut the rod anymore.
if (n ==0) {
return 0;
}
//At any index we have 2 options either
//cut the rod of this length or not cut
//it
let notCut = cutRod(price,index - 1,n);
let cut = Number.MIN_VALUE;
let rod_length = index + 1;
if (rod_length <= n)
cut = price[index]
+ cutRod(price,index,n - rod_length);
return Math.max(notCut, cut);
}
/* Driver program to test above functions */
let arr = [ 1, 5, 8, 9, 10, 17, 17, 20 ];
let size = arr.length;
console.log("Maximum Obtainable Value is "
+ cutRod(arr, size - 1, size));
// This code is contributed by garg28harsh.
# A recursive solution for Rod cutting problem
# Returns the best obtainable price for a rod of length n
# and price[] as prices of different pieces
def cutRod(price, index, n):
# base case
if index == 0:
return n*price[0]
#v if n is 0 we cannot cut the rod anymore.
if (n ==0):
return 0
# At any index we have 2 options either
# cut the rod of this length or not cut
# it
notCut = cutRod(price,index - 1,n)
cut = float("-inf")
rod_length = index + 1
if (rod_length <= n):
cut = price[index]+cutRod(price,index,n - rod_length)
return max(notCut, cut)
# Driver program to test above functions
arr = [ 1, 5, 8, 9, 10, 17, 17, 20 ]
size = len(arr)
print("Maximum Obtainable Value is ",cutRod(arr, size - 1, size))
# This code is contributed by Vivek Maddeshiya
OutputMaximum Obtainable Value is 22
Time Complexity: O(2n) where n is the length of the price array.
Space Complexity: O(n) where n is the length of the price array.
2) Overlapping Subproblems:
The following is a simple recursive implementation of the Rod Cutting problem.
The implementation simply follows the recursive structure mentioned above.
C++
// A memoization solution for Rod cutting problem
#include <bits/stdc++.h>
#include <iostream>
#include <math.h>
using namespace std;
// A utility function to get the maximum of two integers
int max(int a, int b) { return (a > b) ? a : b; }
/* Returns the best obtainable price for a rod of length n
and price[] as prices of different pieces */
int cutRod(int price[], int index, int n,
vector<vector<int> >& dp)
{
// base case
if (index == 0) {
return n * price[0];
}
if (dp[index][n] != -1)
return dp[index][n];
// At any index we have 2 options either
// cut the rod of this length or not cut
// it
int notCut = cutRod(price, index - 1, n,dp);
int cut = INT_MIN;
int rod_length = index + 1;
if (rod_length <= n)
cut = price[index]
+ cutRod(price, index, n - rod_length,dp);
return dp[index][n]=max(notCut, cut);
}
/* Driver program to test above functions */
int main()
{
int arr[] = { 1, 5, 8, 9, 10, 17, 17, 20 };
int size = sizeof(arr) / sizeof(arr[0]);
vector<vector<int> > dp(size,
vector<int>(size + 1, -1));
cout << "Maximum Obtainable Value is "
<< cutRod(arr, size - 1, size, dp);
getchar();
return 0;
}
// This code is contributed by Sanskar
// A memoization solution for Rod cutting problem
import java.io.*;
import java.util.*;
/* Returns the best obtainable price for a rod of length n
and price[] as prices of different pieces */
class GFG {
private static int cutRod(int price[], int index, int n,
int[][] dp)
{
// base case
if (index == 0) {
return n * price[0];
}
if (dp[index][n] != -1) {
return dp[index][n];
}
// At any index we have 2 options either
// cut the rod of this length or not cut
// it
int notCut = cutRod(price, index - 1, n, dp);
int cut = Integer.MIN_VALUE;
int rod_length = index + 1;
if (rod_length <= n) {
cut = price[index]
+ cutRod(price, index, n - rod_length,
dp);
}
return dp[index][n] = Math.max(cut, notCut);
}
/* Driver program to test above functions */
public static void main(String[] args)
{
int arr[] = { 1, 5, 8, 9, 10, 17, 17, 20 };
int size = arr.length;
int dp[][] = new int[size][size + 1];
for (int i = 0; i < size; i++) {
Arrays.fill(dp[i], -1);
}
System.out.println(
"Maximum Obtainable Value is "
+ cutRod(arr, size - 1, size, dp));
}
}
// This code is contributed by Snigdha Patil
// A memoization solution for Rod cutting problem
using System;
public class HelloWorld
{
// Returns the best obtainable price for
// a rod of length n and price[] as prices of different pieces
private static int cutRod(int[] price, int index,
int n, int[,] dp)
{
// base case
if (index == 0) {
return n * price[0];
}
if (dp[index, n] != -1) {
return dp[index, n];
}
// At any index we have 2 options either cut
// the rod of this length or not cut it
int notCut = cutRod(price, index - 1, n, dp);
int cut = Int32.MinValue;
int rod_length = index + 1;
if (rod_length <= n) {
cut = price[index] + cutRod(price, index, n - rod_length, dp);
}
return dp[index, n] = Math.Max(cut, notCut);
}
// Driver program to test above functions
public static void Main(string[] args) {
int[] arr = { 1, 5, 8, 9, 10, 17, 17, 20 };
int size = arr.Length;
int[,] dp = new int[size, size + 1];
for (int i = 0; i < size; i++) {
for (int j = 0; j < size + 1; j++) {
dp[i, j] = -1;
}
}
Console.WriteLine("Maximum Obtainable Value is " +
cutRod(arr, size - 1, size, dp));
}
}
// This code is contributed by ajaymakvana.
// A memoization solution for Rod cutting problem
// A utility function to get the maximum of two integers
function max(a, b) {
return (a > b) ? a : b;
}
/* Returns the best obtainable price for a rod of length n
and price[] as prices of different pieces */
function cutRod(price, index, n, dp) {
// base case
if (index === 0) {
return n * price[0];
}
if (dp[index][n] !== -1)
return dp[index][n];
// At any index we have 2 options either
// cut the rod of this length or not cut
// it
let notCut = cutRod(price, index - 1, n, dp);
let cut = Number.MIN_SAFE_INTEGER;
let rod_length = index + 1;
if (rod_length <= n)
cut = price[index] + cutRod(price, index, n - rod_length, dp);
return dp[index][n] = max(notCut, cut);
}
/* Driver program to test above functions */
function main() {
let arr = [ 1, 5, 8, 9, 10, 17, 17, 20 ];
let size = arr.length;
let dp = new Array(size);
for (let i = 0; i < size; i++) {
dp[i] = new Array(size + 1).fill(-1);
}
console.log("Maximum Obtainable Value is " + cutRod(arr, size - 1, size, dp));
return 0;
}
main();
# A memoization solution for Rod cutting problem
# Returns the best obtainable price for
# a rod of length n and price[] as
# prices of different pieces
def cutRoad(price,index,n,dp):
# base case
if(index == 0):
return n*price[0]
if(dp[index][n] != -1):
return dp[index][n]
# At any index we have 2 options either
# cut the rod of this length or not cut it
notCut = cutRoad(price,index-1,n,dp)
cut = -5
rod_length = index + 1
if(rod_length <= n):
cut = price[index] + cutRoad(price,index,n-rod_length,dp)
dp[index][n] = max(notCut,cut)
return dp[index][n]
# Driver program to test above functions
if __name__ == "__main__":
arr = [1,5,8,9,10,17,17,20]
size = len(arr)
dp = []
temp = []
for i in range(0,size+1):
temp.append(-1)
for i in range(0,size):
dp.append(temp)
# print(dp)
print("Maximum Obtainable Value is :",end=' ')
print(cutRoad(arr,size-1,size,dp))
OutputMaximum Obtainable Value is 22
Time Complexity: O(n2)
Auxiliary Space: O(n2)+O(n)
Considering the above implementation, the following is the recursion tree for a Rod of length 4.
cR() ---> cutRod()
cR(4)
/ /
/ /
cR(3) cR(2) cR(1) cR(0)
/ | / |
/ | / |
cR(2) cR(1) cR(0) cR(1) cR(0) cR(0)
/ | |
/ | |
cR(1) cR(0) cR(0) cR(0)
/
/
CR(0)
In the above partial recursion tree, cR(2) is solved twice. We can see that there are many subproblems that are solved again and again. Since the same subproblems are called again, this problem has the Overlapping Subproblems property. So the Rod Cutting problem has both properties (see this and this) of a dynamic programming problem. Like other typical Dynamic Programming(DP) problems, recomputations of the same subproblems can be avoided by constructing a temporary array val[] in a bottom-up manner.
C++
// A Dynamic Programming solution for Rod cutting problem
#include<iostream>
#include <bits/stdc++.h>
#include<math.h>
using namespace std;
// A utility function to get the maximum of two integers
int max(int a, int b) { return (a > b)? a : b;}
/* Returns the best obtainable price for a rod of length n and
price[] as prices of different pieces */
int cutRod(int price[], int n)
{
int val[n+1];
val[0] = 0;
int i, j;
// Build the table val[] in bottom up manner and return the last entry
// from the table
for (i = 1; i<=n; i++)
{
int max_val = INT_MIN;
for (j = 0; j < i; j++)
max_val = max(max_val, price[j] + val[i-j-1]);
val[i] = max_val;
}
return val[n];
}
/* Driver program to test above functions */
int main()
{
int arr[] = {1, 5, 8, 9, 10, 17, 17, 20};
int size = sizeof(arr)/sizeof(arr[0]);
cout <<"Maximum Obtainable Value is "<<cutRod(arr, size);
getchar();
return 0;
}
// This code is contributed by shivanisinghss2110
// A Dynamic Programming solution for Rod cutting problem
#include<stdio.h>
#include<limits.h>
// A utility function to get the maximum of two integers
int max(int a, int b) { return (a > b)? a : b;}
/* Returns the best obtainable price for a rod of length n and
price[] as prices of different pieces */
int cutRod(int price[], int n)
{
int val[n+1];
val[0] = 0;
int i, j;
// Build the table val[] in bottom up manner and return the last entry
// from the table
for (i = 1; i<=n; i++)
{
int max_val = INT_MIN;
for (j = 0; j < i; j++)
max_val = max(max_val, price[j] + val[i-j-1]);
val[i] = max_val;
}
return val[n];
}
/* Driver program to test above functions */
int main()
{
int arr[] = {1, 5, 8, 9, 10, 17, 17, 20};
int size = sizeof(arr)/sizeof(arr[0]);
printf("Maximum Obtainable Value is %d", cutRod(arr, size));
getchar();
return 0;
}
// A Dynamic Programming solution for Rod cutting problem
import java.io.*;
class RodCutting
{
/* Returns the best obtainable price for a rod of
length n and price[] as prices of different pieces */
static int cutRod(int price[],int n)
{
int val[] = new int[n+1];
val[0] = 0;
// Build the table val[] in bottom up manner and return
// the last entry from the table
for (int i = 1; i<=n; i++)
{
int max_val = Integer.MIN_VALUE;
for (int j = 0; j < i; j++)
max_val = Math.max(max_val,
price[j] + val[i-j-1]);
val[i] = max_val;
}
return val[n];
}
/* Driver program to test above functions */
public static void main(String args[])
{
int arr[] = new int[] {1, 5, 8, 9, 10, 17, 17, 20};
int size = arr.length;
System.out.println("Maximum Obtainable Value is " +
cutRod(arr, size));
}
}
/* This code is contributed by Rajat Mishra */
// A Dynamic Programming solution
// for Rod cutting problem
using System;
class GFG {
/* Returns the best obtainable
price for a rod of length n
and price[] as prices of
different pieces */
static int cutRod(int []price,int n)
{
int []val = new int[n + 1];
val[0] = 0;
// Build the table val[] in
// bottom up manner and return
// the last entry from the table
for (int i = 1; i<=n; i++)
{
int max_val = int.MinValue;
for (int j = 0; j < i; j++)
max_val = Math.Max(max_val,
price[j] + val[i - j - 1]);
val[i] = max_val;
}
return val[n];
}
// Driver Code
public static void Main()
{
int []arr = new int[] {1, 5, 8, 9, 10, 17, 17, 20};
int size = arr.Length;
Console.WriteLine("Maximum Obtainable Value is " +
cutRod(arr, size));
}
}
// This code is contributed by Sam007
<script>
// A Dynamic Programming solution
// for Rod cutting problem
/* Returns the best obtainable
price for a rod of length n
and price[] as prices of
different pieces */
function cutRod(price, n)
{
let val = new Array(n + 1);
val[0] = 0;
// Build the table val[] in
// bottom up manner and return
// the last entry from the table
for (let i = 1; i<=n; i++)
{
let max_val = Number.MIN_VALUE;
for (let j = 0; j < i; j++)
max_val = Math.max(max_val, price[j] + val[i - j - 1]);
val[i] = max_val;
}
return val[n];
}
let arr = [1, 5, 8, 9, 10, 17, 17, 20];
let size = arr.length;
document.write("Maximum Obtainable Value is " + cutRod(arr, size) + "n");
</script>
<?php
// A Dynamic Programming solution for
// Rod cutting problem
/* Returns the best obtainable price
for a rod of length n and price[] as
prices of different pieces */
function cutRod( $price, $n)
{
$val = array();
$val[0] = 0;
$i; $j;
// Build the table val[] in bottom
// up manner and return the last
// entry from the table
for ($i = 1; $i <= $n; $i++)
{
$max_val = PHP_INT_MIN;
for ($j = 0; $j < $i; $j++)
$max_val = max($max_val,
$price[$j] + $val[$i-$j-1]);
$val[$i] = $max_val;
}
return $val[$n];
}
// Driver program to test above functions
$arr = array(1, 5, 8, 9, 10, 17, 17, 20);
$size = count($arr);
echo "Maximum Obtainable Value is ",
cutRod($arr, $size);
// This code is contributed by anuj_67.
?>
# A Dynamic Programming solution for Rod cutting problem
INT_MIN = -32767
# Returns the best obtainable price for a rod of length n and
# price[] as prices of different pieces
def cutRod(price, n):
val = [0 for x in range(n+1)]
val[0] = 0
# Build the table val[] in bottom up manner and return
# the last entry from the table
for i in range(1, n+1):
max_val = INT_MIN
for j in range(i):
max_val = max(max_val, price[j] + val[i-j-1])
val[i] = max_val
return val[n]
# Driver program to test above functions
arr = [1, 5, 8, 9, 10, 17, 17, 20]
size = len(arr)
print("Maximum Obtainable Value is " + str(cutRod(arr, size)))
# This code is contributed by Bhavya Jain
OutputMaximum Obtainable Value is 22
The Time Complexity of the above implementation is O(n^2), which is much better than the worst-case time complexity of Naive Recursive implementation.
Space Complexity: O(n) as val array has been created.
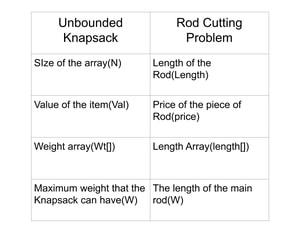
3) Using the idea of Unbounded Knapsack.
This problem is very similar to the Unbounded Knapsack Problem, where there are multiple occurrences of the same item. Here the pieces of the rod. Now I will create an analogy between Unbounded Knapsack and the Rod Cutting Problem.
C++
// CPP program for above approach
#include <iostream>
using namespace std;
// Global Array for
// the purpose of memoization.
int t[9][9];
// A recursive program, using ,
// memoization, to implement the
// rod cutting problem(Top-Down).
int un_kp(int price[], int length[],
int Max_len, int n)
{
// The maximum price will be zero,
// when either the length of the rod
// is zero or price is zero.
if (n == 0 || Max_len == 0)
{
return 0;
}
// If the length of the rod is less
// than the maximum length, Max_lene will
// consider it.Now depending
// upon the profit,
// either Max_lene we will take
// it or discard it.
if (length[n - 1] <= Max_len)
{
t[n][Max_len]
= max(price[n - 1]
+ un_kp(price, length,
Max_len - length[n - 1], n),
un_kp(price, length, Max_len, n - 1));
}
// If the length of the rod is
// greater than the permitted size,
// Max_len we will not consider it.
else
{
t[n][Max_len]
= un_kp(price, length,
Max_len, n - 1);
}
// Max_lene Max_lenill return the maximum
// value obtained, Max_lenhich is present
// at the nth roMax_len and Max_length column.
return t[n][Max_len];
}
/* Driver program to
test above functions */
int main()
{
int price[] = { 1, 5, 8, 9, 10, 17, 17, 20 };
int n = sizeof(price) / sizeof(price[0]);
int length[n];
for (int i = 0; i < n; i++) {
length[i] = i + 1;
}
int Max_len = n;
// Function Call
cout << "Maximum obtained value is "
<< un_kp(price, length, n, Max_len) << endl;
}
// C program for above approach
#include <stdio.h>
#include <stdlib.h>
int max(int a, int b)
{
return (a > b) ? a : b;
}
// Global Array for the
// purpose of memoization.
int t[9][9];
// A recursive program, using ,
// memoization, to implement the
// rod cutting problem(Top-Down).
int un_kp(int price[], int length[],
int Max_len, int n)
{
// The maximum price will be zero,
// when either the length of the rod
// is zero or price is zero.
if (n == 0 || Max_len == 0)
{
return 0;
}
// If the length of the rod is less
// than the maximum length, Max_lene
// will consider it.Now depending
// upon the profit,
// either Max_lene we will take it
// or discard it.
if (length[n - 1] <= Max_len)
{
t[n][Max_len]
= max(price[n - 1]
+ un_kp(price, length,
Max_len - length[n - 1], n),
un_kp(price, length, Max_len, n - 1));
}
// If the length of the rod is greater
// than the permitted size, Max_len
// we will not consider it.
else
{
t[n][Max_len]
= un_kp(price, length,
Max_len, n - 1);
}
// Max_lene Max_lenill return
// the maximum value obtained,
// Max_lenhich is present at the
// nth roMax_len and Max_length column.
return t[n][Max_len];
}
/* Driver program to test above functions */
int main()
{
int price[] = { 1, 5, 8, 9, 10, 17, 17, 20 };
int n = sizeof(price) / sizeof(price[0]);
int length[n];
for (int i = 0; i < n; i++)
{
length[i] = i + 1;
}
int Max_len = n;
// Function Call
printf("Maximum obtained value is %d \n",
un_kp(price, length, n, Max_len));
}
// Java program for above approach
import java.io.*;
class GFG {
// Global Array for
// the purpose of memoization.
static int t[][] = new int[9][9];
// A recursive program, using ,
// memoization, to implement the
// rod cutting problem(Top-Down).
public static int un_kp(int price[], int length[],
int Max_len, int n)
{
// The maximum price will be zero,
// when either the length of the rod
// is zero or price is zero.
if (n == 0 || Max_len == 0) {
return 0;
}
// If the length of the rod is less
// than the maximum length, Max_lene will
// consider it.Now depending
// upon the profit,
// either Max_lene we will take
// it or discard it.
if (length[n - 1] <= Max_len) {
t[n][Max_len] = Math.max(
price[n - 1]
+ un_kp(price, length,
Max_len - length[n - 1], n),
un_kp(price, length, Max_len, n - 1));
}
// If the length of the rod is
// greater than the permitted size,
// Max_len we will not consider it.
else {
t[n][Max_len]
= un_kp(price, length, Max_len, n - 1);
}
// Max_lene Max_lenill return the maximum
// value obtained, Max_lenhich is present
// at the nth roMax_len and Max_length column.
return t[n][Max_len];
}
public static void main(String[] args)
{
int price[]
= new int[] { 1, 5, 8, 9, 10, 17, 17, 20 };
int n = price.length;
int length[] = new int[n];
for (int i = 0; i < n; i++) {
length[i] = i + 1;
}
int Max_len = n;
System.out.println(
"Maximum obtained value is "
+ un_kp(price, length, n, Max_len));
}
}
// This code is contributed by rajsanghavi9.
// C# program for above approach
using System;
public class GFG {
// Global Array for
// the purpose of memoization.
static int [,]t = new int[9,9];
// A recursive program, using ,
// memoization, to implement the
// rod cutting problem(Top-Down).
public static int un_kp(int []price, int []length, int Max_len, int n) {
// The maximum price will be zero,
// when either the length of the rod
// is zero or price is zero.
if (n == 0 || Max_len == 0) {
return 0;
}
// If the length of the rod is less
// than the maximum length, Max_lene will
// consider it.Now depending
// upon the profit,
// either Max_lene we will take
// it or discard it.
if (length[n - 1] <= Max_len) {
t[n,Max_len] = Math.Max(price[n - 1] + un_kp(price, length, Max_len - length[n - 1], n),
un_kp(price, length, Max_len, n - 1));
}
// If the length of the rod is
// greater than the permitted size,
// Max_len we will not consider it.
else {
t[n,Max_len] = un_kp(price, length, Max_len, n - 1);
}
// Max_lene Max_lenill return the maximum
// value obtained, Max_lenhich is present
// at the nth roMax_len and Max_length column.
return t[n,Max_len];
}
// Driver code
public static void Main(String[] args) {
int []price = new int[] { 1, 5, 8, 9, 10, 17, 17, 20 };
int n = price.Length;
int []length = new int[n];
for (int i = 0; i < n; i++) {
length[i] = i + 1;
}
int Max_len = n;
Console.WriteLine("Maximum obtained value is " + un_kp(price, length, n, Max_len));
}
}
// This code is contributed by gauravrajput1.
<script>
// Javascript program for above approach
// Global Array for
// the purpose of memoization.
let t = new Array(9);
for (var i = 0; i < t.length; i++) {
t[i] = new Array(2);
}
// A recursive program, using ,
// memoization, to implement the
// rod cutting problem(Top-Down).
function un_kp(price, length, Max_len, n)
{
// The maximum price will be zero,
// when either the length of the rod
// is zero or price is zero.
if (n == 0 || Max_len == 0)
{
return 0;
}
// If the length of the rod is less
// than the maximum length, Max_lene will
// consider it.Now depending
// upon the profit,
// either Max_lene we will take
// it or discard it.
if (length[n - 1] <= Max_len)
{
t[n][Max_len]
= Math.max(price[n - 1]
+ un_kp(price, length,
Max_len - length[n - 1], n),
un_kp(price, length, Max_len, n - 1));
}
// If the length of the rod is
// greater than the permitted size,
// Max_len we will not consider it.
else
{
t[n][Max_len]
= un_kp(price, length,
Max_len, n - 1);
}
// Max_lene Max_lenill return the maximum
// value obtained, Max_lenhich is present
// at the nth roMax_len and Max_length column.
return t[n][Max_len];
}
// Driver code
let price = [ 1, 5, 8, 9, 10, 17, 17, 20 ];
let n = price.length;
let length = Array(n).fill(0);
for (let i = 0; i < n; i++) {
length[i] = i + 1;
}
let Max_len = n;
// Function Call
document.write("Maximum obtained value is "
+ un_kp(price, length, n, Max_len));
</script>
# Python program for above approach
# Global Array for
# the purpose of memoization.
t = [[0 for i in range(9)] for j in range(9)]
# A recursive program, using ,
# memoization, to implement the
# rod cutting problem(Top-Down).
def un_kp(price, length, Max_len, n):
# The maximum price will be zero,
# when either the length of the rod
# is zero or price is zero.
if (n == 0 or Max_len == 0):
return 0;
# If the length of the rod is less
# than the maximum length, Max_lene will
# consider it.Now depending
# upon the profit,
# either Max_lene we will take
# it or discard it.
if (length[n - 1] <= Max_len):
t[n][Max_len] = max(price[n - 1] + un_kp(price, length, Max_len - length[n - 1], n),
un_kp(price, length, Max_len, n - 1));
# If the length of the rod is
# greater than the permitted size,
# Max_len we will not consider it.
else:
t[n][Max_len] = un_kp(price, length, Max_len, n - 1);
# Max_lene Max_lenill return the maximum
# value obtained, Max_lenhich is present
# at the nth roMax_len and Max_length column.
return t[n][Max_len];
if __name__ == '__main__':
price = [1, 5, 8, 9, 10, 17, 17, 20 ];
n =len(price);
length = [0]*n;
for i in range(n):
length[i] = i + 1;
Max_len = n;
print("Maximum obtained value is " ,un_kp(price, length, n, Max_len));
# This code is contributed by gauravrajput1
OutputMaximum obtained value is 22
Time Complexity: O(n2)
Auxiliary Space: O(n), since n extra space has been taken.
4) Dynamic Programming Approach Iterative Solution
We will divide the problem into smaller sub-problems. Then using a 2-D matrix, we will calculate the maximum price we can achieve for any particular weight
C++
#include <algorithm>
#include <iostream>
using namespace std;
int cutRod(int prices[], int n)
{
int mat[n + 1][n + 1];
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= n; j++) {
if (i == 0 || j == 0) {
mat[i][j] = 0;
}
else {
if (i == 1) {
mat[i][j] = j * prices[i - 1];
}
else {
if (i > j) {
mat[i][j] = mat[i - 1][j];
}
else {
mat[i][j] = max(prices[i - 1]
+ mat[i][j - i],
mat[i - 1][j]);
}
}
}
}
}
return mat[n][n];
}
int main()
{
int prices[] = { 1, 5, 8, 9, 10, 17, 17, 20 };
int n = sizeof(prices) / sizeof(prices[0]);
cout << "Maximum obtained value is "
<< cutRod(prices, n) << endl;
}
// Java program for above approach
import java.io.*;
class GFG {
public static int cutRod(int prices[], int n)
{
int mat[][] = new int[n + 1][n + 1];
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= n; j++) {
if (i == 0 || j == 0) {
mat[i][j] = 0;
}
else {
if (i == 1) {
mat[i][j] = j * prices[i - 1];
}
else {
if (i > j) {
mat[i][j] = mat[i - 1][j];
}
else {
mat[i][j] = Math.max(
prices[i - 1]
+ mat[i][j - i],
mat[i - 1][j]);
}
}
}
}
}
return mat[n][n];
}
public static void main(String[] args)
{
int prices[]
= new int[] { 1, 5, 8, 9, 10, 17, 17, 20 };
int n = prices.length;
System.out.println("Maximum obtained value is "
+ cutRod(prices, n));
}
}
// C# program for above approach
using System;
using System.Collections;
using System.Collections.Generic;
class GFG {
public static int cutRod(int[] prices, int n)
{
int[, ] mat = new int[n + 1, n + 1];
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= n; j++) {
if (i == 0 || j == 0) {
mat[i, j] = 0;
}
else {
if (i == 1) {
mat[i, j] = j * prices[i - 1];
}
else {
if (i > j) {
mat[i, j] = mat[i - 1, j];
}
else {
mat[i, j] = Math.Max(
prices[i - 1]
+ mat[i, j - i],
mat[i - 1, j]);
}
}
}
}
}
return mat[n, n];
}
public static void Main(string[] args)
{
int[] prices
= new int[] { 1, 5, 8, 9, 10, 17, 17, 20 };
int n = prices.Length;
Console.WriteLine("Maximum obtained value is "
+ cutRod(prices, n));
}
}
// This code is contributed by Karandeep1234
// Javascript implementation of the above C++ code
function cutRod(prices, n) {
// Initialize the matrix with all values as 0
let mat = new Array(n + 1).fill(0).map(() => new Array(n + 1).fill(0));
// Iterate over the matrix
for (let i = 0; i <= n; i++) {
for (let j = 0; j <= n; j++) {
if (i === 0 || j === 0) {
mat[i][j] = 0;
} else {
if (i === 1) {
mat[i][j] = j * prices[i - 1];
} else {
if (i > j) {
mat[i][j] = mat[i - 1][j];
} else {
mat[i][j] = Math.max(prices[i - 1] + mat[i][j - i], mat[i - 1][j]);
}
}
}
}
}
// Return the last element of the matrix
return mat[n][n];
}
// Given prices array
let prices = [1, 5, 8, 9, 10, 17, 17, 20];
let n = prices.length;
console.log("Maximum obtained value is " + cutRod(prices, n));
# Python program for above approach
def cutRod(prices, n):
mat = [[0 for i in range(n+1)]for j in range(n+1)]
for i in range(1, n+1):
for j in range(1, n+1):
if i == 1:
mat[i][j] = j*prices[i-1]
else:
if i > j:
mat[i][j] = mat[i-1][j]
else:
mat[i][j] = max(prices[i-1]+mat[i][j-i], mat[i-1][j])
return mat[n][n]
prices = [1, 5, 8, 9, 10, 17, 17, 20]
n = len(prices)
print("Maximum obtained value is ", cutRod(prices, n))
# This Code is Contributed By Vivek Maddeshiya
OutputMaximum obtained value is 22
Time Complexity: O(n2)
Auxiliary Space: O(n2)
Share your thoughts in the comments
Please Login to comment...