Min Cost Path | DP-6
Last Updated :
09 Oct, 2023
Given a cost matrix cost[][] and a position (M, N) in cost[][], write a function that returns cost of minimum cost path to reach (M, N) from (0, 0). Each cell of the matrix represents a cost to traverse through that cell. The total cost of a path to reach (M, N) is the sum of all the costs on that path (including both source and destination). You can only traverse down, right and diagonally lower cells from a given cell, i.e., from a given cell (i, j), cells (i+1, j), (i, j+1), and (i+1, j+1) can be traversed.
Note: You may assume that all costs are positive integers.
Example:
Input:
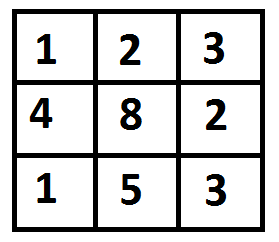
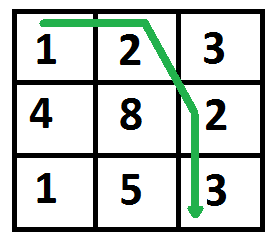
The path with minimum cost is highlighted in the following figure. The path is (0, 0) –> (0, 1) –> (1, 2) –> (2, 2). The cost of the path is 8 (1 + 2 + 2 + 3).
Output:
Min cost path using recursion:
To solve the problem follow the below idea:
This problem has the optimal substructure property. The path to reach (m, n) must be through one of the 3 cells: (m-1, n-1) or (m-1, n) or (m, n-1). So minimum cost to reach (m, n) can be written as “minimum of the 3 cells plus cost[m][n]”.
minCost(m, n) = min (minCost(m-1, n-1), minCost(m-1, n), minCost(m, n-1)) + cost[m][n]
Follow the below steps to solve the problem:
- If N is less than zero or M is less than zero then return Integer Maximum(Base Case)
- If M is equal to zero and N is equal to zero then return cost[M][N](Base Case)
- Return cost[M][N] + minimum of (minCost(M-1, N-1), minCost(M-1, N), minCost(M, N-1))
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
#define R 3
#define C 3
int min(int x, int y, int z);
int minCost(int cost[R][C], int m, int n)
{
if (n < 0 || m < 0)
return INT_MAX;
else if (m == 0 && n == 0)
return cost[m][n];
else
return cost[m][n]
+ min(minCost(cost, m - 1, n - 1),
minCost(cost, m - 1, n),
minCost(cost, m, n - 1));
}
int min(int x, int y, int z)
{
if (x < y)
return (x < z) ? x : z;
else
return (y < z) ? y : z;
}
int main()
{
int cost[R][C]
= { { 1, 2, 3 }, { 4, 8, 2 }, { 1, 5, 3 } };
cout << minCost(cost, 2, 2) << endl;
return 0;
}
|
C
#include <limits.h>
#include <stdio.h>
#define R 3
#define C 3
int min(int x, int y, int z);
int minCost(int cost[R][C], int m, int n)
{
if (n < 0 || m < 0)
return INT_MAX;
else if (m == 0 && n == 0)
return cost[m][n];
else
return cost[m][n]
+ min(minCost(cost, m - 1, n - 1),
minCost(cost, m - 1, n),
minCost(cost, m, n - 1));
}
int min(int x, int y, int z)
{
if (x < y)
return (x < z) ? x : z;
else
return (y < z) ? y : z;
}
int main()
{
int cost[R][C]
= { { 1, 2, 3 }, { 4, 8, 2 }, { 1, 5, 3 } };
printf(" %d ", minCost(cost, 2, 2));
return 0;
}
|
Java
public class GFG {
static int min(int x, int y, int z)
{
if (x < y)
return (x < z) ? x : z;
else
return (y < z) ? y : z;
}
static int minCost(int cost[][], int m, int n)
{
if (n < 0 || m < 0)
return Integer.MAX_VALUE;
else if (m == 0 && n == 0)
return cost[m][n];
else
return cost[m][n]
+ min(minCost(cost, m - 1, n - 1),
minCost(cost, m - 1, n),
minCost(cost, m, n - 1));
}
public static void main(String args[])
{
int cost[][]
= { { 1, 2, 3 }, { 4, 8, 2 }, { 1, 5, 3 } };
System.out.print(minCost(cost, 2, 2));
}
}
|
Python3
import sys
R = 3
C = 3
def minCost(cost, m, n):
if (n < 0 or m < 0):
return sys.maxsize
elif (m == 0 and n == 0):
return cost[m][n]
else:
return cost[m][n] + min(minCost(cost, m-1, n-1),
minCost(cost, m-1, n),
minCost(cost, m, n-1))
def min(x, y, z):
if (x < y):
return x if (x < z) else z
else:
return y if (y < z) else z
cost = [[1, 2, 3],
[4, 8, 2],
[1, 5, 3]]
print(minCost(cost, 2, 2))
|
C#
using System;
class GFG {
static int min(int x, int y, int z)
{
if (x < y)
return ((x < z) ? x : z);
else
return ((y < z) ? y : z);
}
static int minCost(int[, ] cost, int m, int n)
{
if (n < 0 || m < 0)
return int.MaxValue;
else if (m == 0 && n == 0)
return cost[m, n];
else
return cost[m, n]
+ min(minCost(cost, m - 1, n - 1),
minCost(cost, m - 1, n),
minCost(cost, m, n - 1));
}
public static void Main()
{
int[, ] cost
= { { 1, 2, 3 }, { 4, 8, 2 }, { 1, 5, 3 } };
Console.Write(minCost(cost, 2, 2));
}
}
|
Javascript
<script>
function min(x, y, z)
{
if (x < y)
return (x < z) ? x : z;
else
return (y < z) ? y : z;
}
function minCost(cost, m, n)
{
if (n < 0 || m < 0)
return Number.MAX_VALUE;
else if (m == 0 && n == 0)
return cost[m][n];
else
return cost[m][n] + min(minCost(cost, m - 1, n - 1),
minCost(cost, m - 1, n),
minCost(cost, m, n - 1));
}
var cost = [ [ 1, 2, 3 ],
[ 4, 8, 2 ],
[ 1, 5, 3 ] ];
document.write(minCost(cost, 2, 2));
</script>
|
PHP
<?php
$R = 3;
$C = 3;
function minCost($cost, $m, $n)
{
global $R;
global $C;
if ($n < 0 || $m < 0)
return PHP_INT_MAX;
else if ($m == 0 && $n == 0)
return $cost[$m][$n];
else
return $cost[$m][$n] +
min1(minCost($cost, $m - 1, $n - 1),
minCost($cost, $m - 1, $n),
minCost($cost, $m, $n - 1) );
}
function min1($x, $y, $z)
{
if ($x < $y)
return ($x < $z)? $x : $z;
else
return ($y < $z)? $y : $z;
}
$cost = array(array(1, 2, 3),
array (4, 8, 2),
array (1, 5, 3));
echo minCost($cost, 2, 2);
?>
|
Time Complexity: O((M * N)3)
Auxiliary Space: O(M + N), for recursive stack space
Min cost path using Memoization DP:
To convert the given recursive implementation to a memoized version, use an auxiliary table to store the already computed values.
An additional 2D array memo is introduced to store the computed values. Initially, all entries of memo are set to -1 using the memset function. The minCostMemoized function is recursively called, and before making a recursive call, it checks if the value has already been computed by checking the corresponding entry in the memo table. If the value is found in the memo table, it is directly returned. Otherwise, the value is computed, stored in the memo table, and returned.
This memoized version will avoid redundant recursive calls and greatly improve the efficiency of the algorithm by storing and reusing previously computed values.
C++
#include <bits/stdc++.h>
using namespace std;
#define R 3
#define C 3
int min(int x, int y, int z);
int minCostMemoized(int cost[R][C], int m, int n,
int memo[R][C])
{
if (n < 0 || m < 0)
return INT_MAX;
else if (m == 0 && n == 0)
return cost[m][n];
if (memo[m][n] != -1)
return memo[m][n];
memo[m][n]
= cost[m][n]
+ min(minCostMemoized(cost, m - 1, n - 1, memo),
minCostMemoized(cost, m - 1, n, memo),
minCostMemoized(cost, m, n - 1, memo));
return memo[m][n];
}
int minCost(int cost[R][C], int m, int n)
{
int memo[R][C];
memset(memo, -1,
sizeof(memo));
return minCostMemoized(cost, m, n, memo);
}
int min(int x, int y, int z)
{
if (x < y)
return (x < z) ? x : z;
else
return (y < z) ? y : z;
}
int main()
{
int cost[R][C]
= { { 1, 2, 3 }, { 4, 8, 2 }, { 1, 5, 3 } };
cout << minCost(cost, 2, 2) << endl;
return 0;
}
|
Java
import java.util.Arrays;
public class MinimumCostPath {
static final int R = 3;
static final int C = 3;
public static int min(int x, int y, int z) {
if (x < y)
return (x < z) ? x : z;
else
return (y < z) ? y : z;
}
public static int minCostMemoized(int[][] cost, int m, int n, int[][] memo) {
if (n < 0 || m < 0)
return Integer.MAX_VALUE;
else if (m == 0 && n == 0)
return cost[m][n];
if (memo[m][n] != -1)
return memo[m][n];
memo[m][n] = cost[m][n]
+ min(minCostMemoized(cost, m - 1, n - 1, memo),
minCostMemoized(cost, m - 1, n, memo),
minCostMemoized(cost, m, n - 1, memo));
return memo[m][n];
}
public static int minCost(int[][] cost, int m, int n) {
int[][] memo = new int[R][C];
for (int[] row : memo)
Arrays.fill(row, -1);
return minCostMemoized(cost, m, n, memo);
}
public static void main(String[] args) {
int[][] cost = { { 1, 2, 3 }, { 4, 8, 2 }, { 1, 5, 3 } };
System.out.println(minCost(cost, 2, 2));
}
}
|
Python3
R = 3
C = 3
def min_cost_memoized(cost, m, n, memo):
if n < 0 or m < 0:
return float('inf')
elif m == 0 and n == 0:
return cost[m][n]
if memo[m][n] != -1:
return memo[m][n]
memo[m][n] = cost[m][n] + min(
min_cost_memoized(cost, m - 1, n - 1, memo),
min_cost_memoized(cost, m - 1, n, memo),
min_cost_memoized(cost, m, n - 1, memo)
)
return memo[m][n]
def min_cost(cost, m, n):
memo = [[-1] * C for _ in range(R)]
return min_cost_memoized(cost, m, n, memo)
cost = [
[1, 2, 3],
[4, 8, 2],
[1, 5, 3]
]
print(min_cost(cost, 2, 2))
|
C#
using System;
class Program {
const int R = 3;
const int C = 3;
static int MinCostMemoized(int[][] cost, int m, int n,
int[][] memo)
{
if (n < 0 || m < 0)
return int.MaxValue;
else if (m == 0 && n == 0)
return cost[m][n];
if (memo[m][n] != -1)
return memo[m][n];
memo[m][n]
= cost[m][n]
+ Math.Min(
Math.Min(MinCostMemoized(cost, m - 1,
n - 1, memo),
MinCostMemoized(cost, m - 1, n,
memo)),
MinCostMemoized(cost, m, n - 1, memo));
return memo[m][n];
}
static int MinCost(int[][] cost, int m, int n)
{
int[][] memo = new int[R][];
for (int i = 0; i < R; i++) {
memo[i] = new int[C];
for (int j = 0; j < C; j++) {
memo[i][j] = -1;
}
}
return MinCostMemoized(cost, m, n, memo);
}
static int Min(int x, int y, int z)
{
if (x < y)
return (x < z) ? x : z;
else
return (y < z) ? y : z;
}
static void Main(string[] args)
{
int[][] cost
= new int[][] { new int[] { 1, 2, 3 },
new int[] { 4, 8, 2 },
new int[] { 1, 5, 3 } };
Console.WriteLine(MinCost(cost, 2, 2));
}
}
|
Javascript
const R = 3;
const C = 3;
function min(x, y, z) {
return (x < y) ? (x < z ? x : z) : (y < z ? y : z);
}
function minCostMemoized(cost, m, n, memo) {
if (n < 0 || m < 0) {
return Number.MAX_SAFE_INTEGER;
}
else if (m === 0 && n === 0) {
return cost[m][n];
}
if (memo[m][n] !== -1) {
return memo[m][n];
}
memo[m][n] = cost[m][n] + min(
minCostMemoized(cost, m - 1, n - 1, memo),
minCostMemoized(cost, m - 1, n, memo),
minCostMemoized(cost, m, n - 1, memo)
);
return memo[m][n];
}
function minCost(cost, m, n) {
const memo = new Array(R).fill().map(() => new Array(C).fill(-1));
return minCostMemoized(cost, m, n, memo);
}
const cost = [
[1, 2, 3],
[4, 8, 2],
[1, 5, 3]
];
console.log(minCost(cost, 2, 2));
|
Time Complexity: O(M * N)
Auxiliary Space: O(M * N)
To solve the problem follow the below idea:
It should be noted that the above function computes the same subproblems again and again. See the following recursion tree, there are many nodes which appear more than once. The time complexity of this naive recursive solution is exponential and it is terribly slow.
mC refers to minCost()
mC(2, 2)
/ | \
/ | \
mC(1, 1) mC(1, 2) mC(2, 1)
/ | \ / | \ / | \
/ | \ / | \ / | \
mC(0,0) mC(0,1) mC(1,0) mC(0,1) mC(0,2) mC(1,1) mC(1,0) mC(1,1) mC(2,0)
So the MCP problem has both properties (see this and this) of a dynamic programming problem. Like other typical Dynamic Programming(DP) problems, recomputations of the same subproblems can be avoided by constructing a temporary array tc[][] in a bottom-up manner.
Follow the below steps to solve the problem:
- Create a 2-D array ‘tc’ of size R * C
- Calculate prefix sum for the first row and first column in ‘tc’ array as there is only one way to reach any cell in the first row or column
- Run a nested for loop for i [1, M] and j [1, N]
- Set tc[i][j] equal to minimum of (tc[i-1][j-1], tc[i-1][j], tc[i][j-1]) + cost[i][j]
- Return tc[M][N]
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
#define R 3
#define C 3
using namespace std;
int min(int x, int y, int z);
int minCost(int cost[R][C], int m, int n)
{
int i, j;
int tc[R][C];
tc[0][0] = cost[0][0];
for (i = 1; i <= m; i++)
tc[i][0] = tc[i - 1][0] + cost[i][0];
for (j = 1; j <= n; j++)
tc[0][j] = tc[0][j - 1] + cost[0][j];
for (i = 1; i <= m; i++)
for (j = 1; j <= n; j++)
tc[i][j] = min(tc[i - 1][j - 1], tc[i - 1][j],
tc[i][j - 1])
+ cost[i][j];
return tc[m][n];
}
int min(int x, int y, int z)
{
if (x < y)
return (x < z) ? x : z;
else
return (y < z) ? y : z;
}
int main()
{
int cost[R][C]
= { { 1, 2, 3 }, { 4, 8, 2 }, { 1, 5, 3 } };
cout << " " << minCost(cost, 2, 2);
return 0;
}
|
C
#include <limits.h>
#include <stdio.h>
#define R 3
#define C 3
int min(int x, int y, int z);
int minCost(int cost[R][C], int m, int n)
{
int i, j;
int tc[R][C];
tc[0][0] = cost[0][0];
for (i = 1; i <= m; i++)
tc[i][0] = tc[i - 1][0] + cost[i][0];
for (j = 1; j <= n; j++)
tc[0][j] = tc[0][j - 1] + cost[0][j];
for (i = 1; i <= m; i++)
for (j = 1; j <= n; j++)
tc[i][j] = min(tc[i - 1][j - 1], tc[i - 1][j],
tc[i][j - 1])
+ cost[i][j];
return tc[m][n];
}
int min(int x, int y, int z)
{
if (x < y)
return (x < z) ? x : z;
else
return (y < z) ? y : z;
}
int main()
{
int cost[R][C]
= { { 1, 2, 3 }, { 4, 8, 2 }, { 1, 5, 3 } };
printf(" %d ", minCost(cost, 2, 2));
return 0;
}
|
Java
import java.util.*;
class MinimumCostPath {
private static int min(int x, int y, int z)
{
if (x < y)
return (x < z) ? x : z;
else
return (y < z) ? y : z;
}
private static int minCost(int cost[][], int m, int n)
{
int i, j;
int tc[][] = new int[m + 1][n + 1];
tc[0][0] = cost[0][0];
for (i = 1; i <= m; i++)
tc[i][0] = tc[i - 1][0] + cost[i][0];
for (j = 1; j <= n; j++)
tc[0][j] = tc[0][j - 1] + cost[0][j];
for (i = 1; i <= m; i++)
for (j = 1; j <= n; j++)
tc[i][j] = min(tc[i - 1][j - 1],
tc[i - 1][j], tc[i][j - 1])
+ cost[i][j];
return tc[m][n];
}
public static void main(String args[])
{
int cost[][]
= { { 1, 2, 3 }, { 4, 8, 2 }, { 1, 5, 3 } };
System.out.println(minCost(cost, 2, 2));
}
}
|
Python
R = 3
C = 3
def minCost(cost, m, n):
tc = [[0 for x in range(C)] for x in range(R)]
tc[0][0] = cost[0][0]
for i in range(1, m+1):
tc[i][0] = tc[i-1][0] + cost[i][0]
for j in range(1, n+1):
tc[0][j] = tc[0][j-1] + cost[0][j]
for i in range(1, m+1):
for j in range(1, n+1):
tc[i][j] = min(tc[i-1][j-1], tc[i-1][j], tc[i][j-1]) + cost[i][j]
return tc[m][n]
cost = [[1, 2, 3],
[4, 8, 2],
[1, 5, 3]]
print(minCost(cost, 2, 2))
|
C#
using System;
class GFG {
private static int min(int x, int y, int z)
{
if (x < y)
return (x < z) ? x : z;
else
return (y < z) ? y : z;
}
private static int minCost(int[, ] cost, int m, int n)
{
int i, j;
int[, ] tc = new int[m + 1, n + 1];
tc[0, 0] = cost[0, 0];
for (i = 1; i <= m; i++)
tc[i, 0] = tc[i - 1, 0] + cost[i, 0];
for (j = 1; j <= n; j++)
tc[0, j] = tc[0, j - 1] + cost[0, j];
for (i = 1; i <= m; i++)
for (j = 1; j <= n; j++)
tc[i, j] = min(tc[i - 1, j - 1],
tc[i - 1, j], tc[i, j - 1])
+ cost[i, j];
return tc[m, n];
}
public static void Main()
{
int[, ] cost
= { { 1, 2, 3 }, { 4, 8, 2 }, { 1, 5, 3 } };
Console.Write(minCost(cost, 2, 2));
}
}
|
Javascript
<script>
function min(x, y, z)
{
if (x < y)
return (x < z)? x : z;
else
return (y < z)? y : z;
}
function minCost(cost, m, n)
{
let i, j;
let tc = new Array(m+1);
for(let k = 0; k < m + 1; k++)
{
tc[k] = new Array(n+1);
}
tc[0][0] = cost[0][0];
for (i = 1; i <= m; i++)
tc[i][0] = tc[i-1][0] + cost[i][0];
for (j = 1; j <= n; j++)
tc[0][j] = tc[0][j-1] + cost[0][j];
for (i = 1; i <= m; i++)
for (j = 1; j <= n; j++)
tc[i][j] = Math.min(tc[i-1][j-1],
tc[i-1][j],
tc[i][j-1]) + cost[i][j];
return tc[m][n];
}
let cost = [[1, 2, 3],
[4, 8, 2],
[1, 5, 3]];
document.write(minCost(cost,2,2));
</script>
|
PHP
<?php
$R = 3;
$C = 3;
function minCost($cost, $m, $n)
{
global $R;
global $C;
$tc;
for ($i = 0; $i <= $R; $i++)
for ($j = 0; $j <= $C; $j++)
$tc[$i][$j] = 0;
$tc[0][0] = $cost[0][0];
for ($i = 1; $i <= $m; $i++)
$tc[$i][0] = $tc[$i - 1][0] +
$cost[$i][0];
for ($j = 1; $j <= $n; $j++)
$tc[0][$j] = $tc[0][$j - 1] +
$cost[0][$j];
for ($i = 1; $i <= $m; $i++)
for ($j = 1; $j <= $n; $j++)
$tc[$i][$j] = min($tc[$i - 1][$j - 1],
$tc[$i - 1][$j],
$tc[$i][$j - 1]) +
$cost[$i][$j];
return $tc[$m][$n];
}
$cost = array(array(1, 2, 3),
array(4, 8, 2),
array(1, 5, 3));
echo minCost($cost, 2, 2);
?>
|
Time Complexity: O(M * N)
Auxiliary Space: O(M * N)
Min cost path using Dynamic Programming(Space optimized):
To solve the problem follow the below idea:
The idea is to use the same given/input array to store the solutions of subproblems in the above solution
Follow the below steps to solve the problem:
- Calculate prefix sum for the first row and first column in ‘cost’ array as there is only one way to reach any cell in the first row or column
- Run a nested for loop for i [1, M-1] and j [1, N-1]
- Set cost[i][j] equal to minimum of (cost[i-1][j-1], cost[i-1][j], cost[i][j-1]) + cost[i][j]
- Return cost[M-1][N-1]
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
#define row 3
#define col 3
int minCost(int cost[row][col])
{
for (int i = 1; i < row; i++)
cost[i][0] += cost[i - 1][0];
for (int j = 1; j < col; j++)
cost[0][j] += cost[0][j - 1];
for (int i = 1; i < row; i++)
for (int j = 1; j < col; j++)
cost[i][j]
+= min(cost[i - 1][j - 1],
min(cost[i - 1][j], cost[i][j - 1]));
return cost[row - 1][col - 1];
}
int main(int argc, char const* argv[])
{
int cost[row][col]
= { { 1, 2, 3 }, { 4, 8, 2 }, { 1, 5, 3 } };
cout << minCost(cost) << endl;
return 0;
}
|
C
#include <stdio.h>
#define row 3
#define col 3
int min(int num1, int num2)
{
return (num1 > num2) ? num2 : num1;
}
int minCost(int cost[row][col])
{
for (int i = 1; i < row; i++)
cost[i][0] += cost[i - 1][0];
for (int j = 1; j < col; j++)
cost[0][j] += cost[0][j - 1];
for (int i = 1; i < row; i++)
for (int j = 1; j < col; j++)
cost[i][j]
+= min(cost[i - 1][j - 1],
min(cost[i - 1][j], cost[i][j - 1]));
return cost[row - 1][col - 1];
}
int main()
{
int cost[row][col]
= { { 1, 2, 3 }, { 4, 8, 2 }, { 1, 5, 3 } };
printf("%d \n", minCost(cost));
return 0;
}
|
Java
import java.util.*;
class GFG {
static int row = 3;
static int col = 3;
static int minCost(int cost[][])
{
for (int i = 1; i < row; i++) {
cost[i][0] += cost[i - 1][0];
}
for (int j = 1; j < col; j++) {
cost[0][j] += cost[0][j - 1];
}
for (int i = 1; i < row; i++) {
for (int j = 1; j < col; j++) {
cost[i][j]
+= Math.min(cost[i - 1][j - 1],
Math.min(cost[i - 1][j],
cost[i][j - 1]));
}
}
return cost[row - 1][col - 1];
}
public static void main(String[] args)
{
int cost[][]
= { { 1, 2, 3 }, { 4, 8, 2 }, { 1, 5, 3 } };
System.out.print(minCost(cost) + "\n");
}
}
|
Python3
def minCost(cost, row, col):
for i in range(1, row):
cost[i][0] += cost[i - 1][0]
for j in range(1, col):
cost[0][j] += cost[0][j - 1]
for i in range(1, row):
for j in range(1, col):
cost[i][j] += (min(cost[i - 1][j - 1],
min(cost[i - 1][j],
cost[i][j - 1])))
return cost[row - 1][col - 1]
if __name__ == '__main__':
row = 3
col = 3
cost = [[1, 2, 3],
[4, 8, 2],
[1, 5, 3]]
print(minCost(cost, row, col))
|
C#
using System;
class GFG {
static int row = 3;
static int col = 3;
static int minCost(int[, ] cost)
{
for (int i = 1; i < row; i++) {
cost[i, 0] += cost[i - 1, 0];
}
for (int j = 1; j < col; j++) {
cost[0, j] += cost[0, j - 1];
}
for (int i = 1; i < row; i++) {
for (int j = 1; j < col; j++) {
cost[i, j]
+= Math.Min(cost[i - 1, j - 1],
Math.Min(cost[i - 1, j],
cost[i, j - 1]));
}
}
return cost[row - 1, col - 1];
}
public static void Main(String[] args)
{
int[, ] cost
= { { 1, 2, 3 }, { 4, 8, 2 }, { 1, 5, 3 } };
Console.Write(minCost(cost) + "\n");
}
}
|
Javascript
<script>
var row = 3;
var col = 3;
function minCost(cost)
{
for (i = 1; i < row; i++)
{
cost[i][0] += cost[i - 1][0];
}
for (j = 1; j < col; j++)
{
cost[0][j] += cost[0][j - 1];
}
for (i = 1; i < row; i++)
{
for (j = 1; j < col; j++)
{
cost[i][j] += Math.min(cost[i - 1][j - 1],
Math.min(cost[i - 1][j],
cost[i][j - 1]));
}
}
return cost[row - 1][col - 1];
}
var cost = [[1, 2, 3],
[4, 8, 2],
[1, 5, 3] ];
document.write(minCost(cost) + '<br>');
</script>
|
Time Complexity: O(N * M), where N is the number of rows and M is the number of columns
Auxiliary Space: O(1), since no extra space has been taken
To solve the problem follow the below idea:
We can also use the Dijkstra’s shortest path algorithm to find the path with minimum cost
Follow the below steps to solve the problem:
- Create a 2-D dp array to store answer for each cell
- Declare a priority queue to perform dijkstra’s algorithm
- Return dp[M][N]
Below is the implementation of the approach:
C++
#include <bits/stdc++.h>
using namespace std;
#define R 4
#define C 5
int dx[] = { 1, -1, 0, 0, 1, 1, -1, -1 };
int dy[] = { 0, 0, 1, -1, 1, -1, 1, -1 };
struct Cell {
int x;
int y;
int cost;
};
class mycomparison {
public:
bool operator()(const Cell& lhs, const Cell& rhs) const
{
return (lhs.cost > rhs.cost);
}
};
bool isSafe(int x, int y)
{
return x >= 0 && x < R && y >= 0 && y < C;
}
int minCost(int cost[R][C], int m, int n)
{
int dp[R][C];
bool visited[R][C];
for (int i = 0; i < R; i++) {
for (int j = 0; j < C; j++) {
dp[i][j] = INT_MAX;
visited[i][j] = false;
}
}
priority_queue<Cell, vector<Cell>, mycomparison> pq;
dp[0][0] = cost[0][0];
pq.push({ 0, 0, cost[0][0] });
while (!pq.empty()) {
Cell cell = pq.top();
pq.pop();
int x = cell.x;
int y = cell.y;
if (visited[x][y])
continue;
visited[x][y] = true;
for (int i = 0; i < 8; i++) {
int next_x = x + dx[i];
int next_y = y + dy[i];
if (isSafe(next_x, next_y)
&& !visited[next_x][next_y]) {
dp[next_x][next_y]
= min(dp[next_x][next_y],
dp[x][y] + cost[next_x][next_y]);
pq.push(
{ next_x, next_y, dp[next_x][next_y] });
}
}
}
return dp[m][n];
}
int main()
{
int cost[R][C] = { { 1, 8, 8, 1, 5 },
{ 4, 1, 1, 8, 1 },
{ 4, 2, 8, 8, 1 },
{ 1, 5, 8, 8, 1 } };
printf(" %d ", minCost(cost, 3, 4));
return 0;
}
|
Java
import java.util.*;
public class GFG {
static int R = 4;
static int C = 5;
static int dx[] = { 1, -1, 0, 0, 1, 1, -1, -1 };
static int dy[] = { 0, 0, 1, -1, 1, -1, 1, -1 };
static class Cell {
int x;
int y;
int cost;
Cell(int x, int y, int z)
{
this.x = x;
this.y = y;
this.cost = z;
}
}
static boolean isSafe(int x, int y)
{
return x >= 0 && x < R && y >= 0 && y < C;
}
static int minCost(int cost[][], int m, int n)
{
int[][] dp = new int[R][C];
boolean[][] visited = new boolean[R][C];
for (int i = 0; i < R; i++) {
for (int j = 0; j < C; j++) {
dp[i][j] = Integer.MAX_VALUE;
visited[i][j] = false;
}
}
PriorityQueue<Cell> pq
= new PriorityQueue<>((Cell lhs, Cell rhs) -> {
return lhs.cost - rhs.cost;
});
dp[0][0] = cost[0][0];
pq.add(new Cell(0, 0, cost[0][0]));
while (!pq.isEmpty()) {
Cell cell = pq.peek();
pq.remove();
int x = cell.x;
int y = cell.y;
if (visited[x][y])
continue;
visited[x][y] = true;
for (int i = 0; i < 8; i++) {
int next_x = x + dx[i];
int next_y = y + dy[i];
if (isSafe(next_x, next_y)
&& !visited[next_x][next_y]) {
dp[next_x][next_y] = Math.min(
dp[next_x][next_y],
dp[x][y] + cost[next_x][next_y]);
pq.add(new Cell(next_x, next_y,
dp[next_x][next_y]));
}
}
}
return dp[m][n];
}
public static void main(String[] args)
{
int cost[][] = { { 1, 8, 8, 1, 5 },
{ 4, 1, 1, 8, 1 },
{ 4, 2, 8, 8, 1 },
{ 1, 5, 8, 8, 1 } };
System.out.println(minCost(cost, 3, 4));
}
}
|
Python3
R = 4
C = 5
dx = [ 1, -1, 0, 0, 1, 1, -1, -1 ]
dy = [ 0, 0, 1, -1, 1, -1, 1, -1 ]
class Cell():
def __init__(self, x, y, z):
self.x = x
self.y = y
self.cost = z
def isSafe(x, y):
return (x >= 0 and x < R and
y >= 0 and y < C)
def minCost(cost, m, n):
dp = [[0 for x in range(C)] for x in range(R)]
visited = [[False for x in range(C)]
for x in range(R)]
for i in range(R):
for j in range(C):
dp[i][j] = float("Inf")
visited[i][j] = False
pq = []
dp[0][0] = cost[0][0]
pq.append(Cell(0, 0, cost[0][0]))
while(len(pq)):
cell = pq[0]
pq.pop(0)
x = cell.x
y = cell.y
if(visited[x][y]):
continue
visited[x][y] = True
for i in range(8):
next_x = x + dx[i]
next_y = y + dy[i]
if(isSafe(next_x, next_y) and
not visited[next_x][next_y]):
dp[next_x][next_y] = min(dp[next_x][next_y],
dp[x][y] + cost[next_x][next_y])
pq.append(Cell(next_x, next_y,
dp[next_x][next_y]))
return dp[m][n]
cost = [[1, 8, 8, 1, 5],
[4, 1, 1, 8, 1],
[4, 2, 8, 8, 1],
[1, 5, 8, 8, 1]]
print(minCost(cost, 3, 4))
|
C#
using System;
using System.Collections.Generic;
namespace MinCostPath
{
class Cell
{
public int x;
public int y;
public int cost;
public Cell(int x, int y, int cost)
{
this.x = x;
this.y = y;
this.cost = cost;
}
}
class Program
{
static int R = 4;
static int C = 5;
static int[] dx = { 1, -1, 0, 0, 1, 1, -1, -1 };
static int[] dy = { 0, 0, 1, -1, 1, -1, 1, -1 };
static bool isSafe(int x, int y)
{
return (x >= 0 && x < R && y >= 0 && y < C);
}
static int minCost(int[,] cost, int m, int n)
{
int[,] dp = new int[R, C];
bool[,] visited = new bool[R, C];
for (int i = 0; i < R; i++)
{
for (int j = 0; j < C; j++)
{
dp[i, j] = int.MaxValue;
visited[i, j] = false;
}
}
List<Cell> pq = new List<Cell>();
dp[0, 0] = cost[0, 0];
pq.Add(new Cell(0, 0, cost[0, 0]));
while (pq.Count > 0)
{
Cell cell = pq[0];
pq.RemoveAt(0);
int x = cell.x;
int y = cell.y;
if (visited[x, y])
{
continue;
}
visited[x, y] = true;
for (int i = 0; i < 8; i++)
{
int next_x = x + dx[i];
int next_y = y + dy[i];
if (isSafe(next_x, next_y) && !visited[next_x, next_y])
{
dp[next_x, next_y] = Math.Min(dp[next_x, next_y], dp[x, y] + cost[next_x, next_y]);
pq.Add(new Cell(next_x, next_y, dp[next_x, next_y]));
}
}
}
return dp[m, n];
}
static void Main(string[] args)
{
int[,] cost = new int[,]
{
{ 1, 8, 8, 1, 5 },
{ 4, 1, 1, 8, 1 },
{ 4, 2, 8, 8, 1 },
{ 1, 5, 8, 8, 1 }
};
Console.WriteLine(minCost(cost, 3, 4));
}
}
}
|
Javascript
const R = 4;
const C = 5;
const dx = [1, -1, 0, 0, 1, 1, -1, -1];
const dy = [0, 0, 1, -1, 1, -1, 1, -1];
class Cell {
constructor(x, y, cost) {
this.x = x;
this.y = y;
this.cost = cost;
}
}
class PriorityQueue {
constructor() {
this.heap = [];
}
push(cell) {
this.heap.push(cell);
this.heap.sort((a, b) => a.cost - b.cost);
}
pop() {
return this.heap.shift();
}
empty() {
return this.heap.length === 0;
}
}
function isSafe(x, y) {
return x >= 0 && x < R && y >= 0 && y < C;
}
function minCost(cost, m, n) {
const dp = Array(R).fill().map(() => Array(C).fill(Number.MAX_SAFE_INTEGER));
const visited = Array(R).fill().map(() => Array(C).fill(false));
const pq = new PriorityQueue();
dp[0][0] = cost[0][0];
pq.push(new Cell(0, 0, cost[0][0]));
while (!pq.empty()) {
const cell = pq.pop();
const x = cell.x;
const y = cell.y;
if (visited[x][y]) {
continue;
}
visited[x][y] = true;
for (let i = 0; i < 8; i++) {
const next_x = x + dx[i];
const next_y = y + dy[i];
if (isSafe(next_x, next_y) && !visited[next_x][next_y]) {
dp[next_x][next_y] = Math.min(dp[next_x][next_y], dp[x][y] + cost[next_x][next_y]);
pq.push(new Cell(next_x, next_y, dp[next_x][next_y]));
}
}
}
return dp[m][n];
}
const cost = [ [1, 8, 8, 1, 5],
[4, 1, 1, 8, 1],
[4, 2, 8, 8, 1],
[1, 5, 8, 8, 1]
];
console.log(minCost(cost, 3, 4));
|
Time Complexity: O(V + E * logV), where V is (N*M) and E is also (N*M)
Auxiliary Space: O(N * M)
Share your thoughts in the comments
Please Login to comment...