Partition problem | DP-18

The partition problem is to determine whether a given set can be partitioned into two subsets such that the sum of elements in both subsets is the same. 

Examples:

Input: arr[] = {1, 5, 11, 5}
Output: true 
The array can be partitioned as {1, 5, 5} and {11}

Input: arr[] = {1, 5, 3}
Output: false 
The array cannot be partitioned into equal sum sets.

We strongly recommend that you click here and practice it, before moving on to the solution.

The following are the two main steps to solve this problem:

• Calculate the sum of the array. If the sum is odd, there can not be two subsets with an equal sum, so return false. 
• If the sum of the array elements is even, calculate sum/2 and find a subset of the array with a sum equal to sum/2. 
  The first step is simple. The second step is crucial, it can be solved either using recursion or Dynamic Programming.

Partition problem using recursion:

To solve the problem follow the below idea:

Let isSubsetSum(arr, n, sum/2) be the function that returns true if there is a subset of arr[0..n-1] with sum equal to sum/2
The isSubsetSum problem can be divided into two subproblems

•  isSubsetSum() without considering last element (reducing n to n-1)
•  isSubsetSum considering the last element (reducing sum/2 by arr[n-1] and n to n-1)

If any of the above subproblems return true, then return true. 
isSubsetSum (arr, n, sum/2) = isSubsetSum (arr, n-1, sum/2) || isSubsetSum (arr, n-1, sum/2 – arr[n-1])

Follow the below steps to solve the problem:

• First, check if the sum of the elements is even or not
• After checking, call the recursive function isSubsetSum with parameters as input array, array size, and sum/2
  • If the sum is equal to zero then return true (Base case)
  • If n is equal to 0 and sum is not equal to zero then return false (Base case)
  • Check if the value of the last element is greater than the remaining sum then call this function again by removing the last element
  • else call this function again for both the cases stated above and return true, if anyone of them returns true
• Print the answer

Below is the implementation of the above approach:

C++

// A recursive C++ program for partition problem
#include <bits/stdc++.h>
using namespace std;

// A utility function that returns true if there is
// a subset of arr[] with sum equal to given sum
bool isSubsetSum(int arr[], int n, int sum)
{
    // Base Cases
    if (sum == 0)
        return true;
    if (n == 0 && sum != 0)
        return false;

    // If last element is greater than sum, then
    // ignore it
    if (arr[n - 1] > sum)
        return isSubsetSum(arr, n - 1, sum);

    /* else, check if sum can be obtained by any of
        the following
        (a) including the last element
        (b) excluding the last element
    */
    return isSubsetSum(arr, n - 1, sum)
           || isSubsetSum(arr, n - 1, sum - arr[n - 1]);
}

// Returns true if arr[] can be partitioned in two
// subsets of equal sum, otherwise false
bool findPartiion(int arr[], int n)
{
    // Calculate sum of the elements in array
    int sum = 0;
    for (int i = 0; i < n; i++)
        sum += arr[i];

    // If sum is odd, there cannot be two subsets
    // with equal sum
    if (sum % 2 != 0)
        return false;

    // Find if there is subset with sum equal to
    // half of total sum
    return isSubsetSum(arr, n, sum / 2);
}

// Driver code
int main()
{
    int arr[] = { 3, 1, 5, 9, 12 };
    int n = sizeof(arr) / sizeof(arr[0]);

    // Function call
    if (findPartiion(arr, n) == true)
        cout << "Can be divided into two subsets "
                "of equal sum";
    else
        cout << "Can not be divided into two subsets"
                " of equal sum";
    return 0;
}

// This code is contributed by rathbhupendra

C

// A recursive C program for partition problem
#include <stdbool.h>
#include <stdio.h>

// A utility function that returns true if there is
// a subset of arr[] with sum equal to given sum
bool isSubsetSum(int arr[], int n, int sum)
{
    // Base Cases
    if (sum == 0)
        return true;
    if (n == 0 && sum != 0)
        return false;

    // If last element is greater than sum, then
    // ignore it
    if (arr[n - 1] > sum)
        return isSubsetSum(arr, n - 1, sum);

    /* else, check if sum can be obtained by any of
       the following
       (a) including the last element
       (b) excluding the last element
    */
    return isSubsetSum(arr, n - 1, sum)
           || isSubsetSum(arr, n - 1, sum - arr[n - 1]);
}

// Returns true if arr[] can be partitioned in two
//  subsets of equal sum, otherwise false
bool findPartiion(int arr[], int n)
{
    // Calculate sum of the elements in array
    int sum = 0;
    for (int i = 0; i < n; i++)
        sum += arr[i];

    // If sum is odd, there cannot be two subsets
    // with equal sum
    if (sum % 2 != 0)
        return false;

    // Find if there is subset with sum equal to
    // half of total sum
    return isSubsetSum(arr, n, sum / 2);
}

// Driver code
int main()
{
    int arr[] = { 3, 1, 5, 9, 12 };
    int n = sizeof(arr) / sizeof(arr[0]);

    // Function call
    if (findPartiion(arr, n) == true)
        printf("Can be divided into two subsets "
               "of equal sum");
    else
        printf("Can not be divided into two subsets"
               " of equal sum");
    return 0;
}

Java

// A recursive Java solution for partition problem
import java.io.*;

class Partition {
    // A utility function that returns true if there is a
    // subset of arr[] with sum equal to given sum
    static boolean isSubsetSum(int arr[], int n, int sum)
    {
        // Base Cases
        if (sum == 0)
            return true;
        if (n == 0 && sum != 0)
            return false;

        // If last element is greater than sum, then ignore
        // it
        if (arr[n - 1] > sum)
            return isSubsetSum(arr, n - 1, sum);

        /* else, check if sum can be obtained by any of
           the following
        (a) including the last element
        (b) excluding the last element
        */
        return isSubsetSum(arr, n - 1, sum)
            || isSubsetSum(arr, n - 1, sum - arr[n - 1]);
    }

    // Returns true if arr[] can be partitioned in two
    // subsets of equal sum, otherwise false
    static boolean findPartition(int arr[], int n)
    {
        // Calculate sum of the elements in array
        int sum = 0;
        for (int i = 0; i < n; i++)
            sum += arr[i];

        // If sum is odd, there cannot be two subsets
        // with equal sum
        if (sum % 2 != 0)
            return false;

        // Find if there is subset with sum equal to half
        // of total sum
        return isSubsetSum(arr, n, sum / 2);
    }

    // Driver code
    public static void main(String[] args)
    {

        int arr[] = { 3, 1, 5, 9, 12 };
        int n = arr.length;

        // Function call
        if (findPartition(arr, n) == true)
            System.out.println("Can be divided into two "
                               + "subsets of equal sum");
        else
            System.out.println(
                "Can not be divided into "
                + "two subsets of equal sum");
    }
}
/* This code is contributed by Devesh Agrawal */

Python3

# A recursive Python3 program for
# partition problem

# A utility function that returns
# true if there is a subset of
# arr[] with sum equal to given sum


def isSubsetSum(arr, n, sum):
    # Base Cases
    if sum == 0:
        return True
    if n == 0 and sum != 0:
        return False

    # If last element is greater than sum, then
    # ignore it
    if arr[n-1] > sum:
        return isSubsetSum(arr, n-1, sum)

    ''' else, check if sum can be obtained by any of
    the following
    (a) including the last element
    (b) excluding the last element'''

    return isSubsetSum(arr, n-1, sum) or isSubsetSum(arr, n-1, sum-arr[n-1])

# Returns true if arr[] can be partitioned in two
# subsets of equal sum, otherwise false


def findPartion(arr, n):
    # Calculate sum of the elements in array
    sum = 0
    for i in range(0, n):
        sum += arr[i]
    # If sum is odd, there cannot be two subsets
    # with equal sum
    if sum % 2 != 0:
        return false

    # Find if there is subset with sum equal to
    # half of total sum
    return isSubsetSum(arr, n, sum // 2)


# Driver code
if __name__ == '__main__':
  arr = [3, 1, 5, 9, 12]
  n = len(arr)

  # Function call
  if findPartion(arr, n) == True:
      print("Can be divided into two subsets of equal sum")
  else:
      print("Can not be divided into two subsets of equal sum")

# This code is contributed by shreyanshi_arun.

C#

// A recursive C# solution for partition problem
using System;

class GFG {

    // A utility function that returns true if there is a
    // subset of arr[] with sum equal to given sum
    static bool isSubsetSum(int[] arr, int n, int sum)
    {
        // Base Cases
        if (sum == 0)
            return true;
        if (n == 0 && sum != 0)
            return false;

        // If last element is greater than sum, then ignore
        // it
        if (arr[n - 1] > sum)
            return isSubsetSum(arr, n - 1, sum);

        /* else, check if sum can be obtained by any of
        the following
        (a) including the last element
        (b) excluding the last element
        */
        return isSubsetSum(arr, n - 1, sum)
            || isSubsetSum(arr, n - 1, sum - arr[n - 1]);
    }

    // Returns true if arr[] can be partitioned in two
    // subsets of equal sum, otherwise false
    static bool findPartition(int[] arr, int n)
    {
        // Calculate sum of the elements in array
        int sum = 0;
        for (int i = 0; i < n; i++)
            sum += arr[i];

        // If sum is odd, there cannot be two subsets
        // with equal sum
        if (sum % 2 != 0)
            return false;

        // Find if there is subset with sum equal to half
        // of total sum
        return isSubsetSum(arr, n, sum / 2);
    }

    // Driver code
    public static void Main()
    {

        int[] arr = { 3, 1, 5, 9, 12 };
        int n = arr.Length;

        // Function call
        if (findPartition(arr, n) == true)
            Console.Write("Can be divided into two "
                          + "subsets of equal sum");
        else
            Console.Write("Can not be divided into "
                          + "two subsets of equal sum");
    }
}

// This code is contributed by Sam007

PHP

<?php
// A recursive PHP solution for partition problem

// A utility function that returns true if there is
// a subset of arr[] with sum equal to given sum
function isSubsetSum ($arr, $n, $sum)
{
    // Base Cases
    if ($sum == 0)
        return true;
    if ($n == 0 && $sum != 0)
        return false;

    // If last element is greater than
    // sum, then ignore it
    if ($arr[$n - 1] > $sum)
        return isSubsetSum ($arr, $n - 1, $sum);

    /* else, check if sum can be obtained
       by any of the following
        (a) including the last element
        (b) excluding the last element
    */
    return isSubsetSum ($arr, $n - 1, $sum) ||
           isSubsetSum ($arr, $n - 1,
                        $sum - $arr[$n - 1]);
}

// Returns true if arr[] can be partitioned
// in two subsets of equal sum, otherwise false
function findPartiion ($arr, $n)
{
    // Calculate sum of the elements
    // in array
    $sum = 0;
    for ($i = 0; $i < $n; $i++)
    $sum += $arr[$i];

    // If sum is odd, there cannot be
    // two subsets with equal sum
    if ($sum % 2 != 0)
    return false;

    // Find if there is subset with sum
    // equal to half of total sum
    return isSubsetSum ($arr, $n, $sum / 2);
}

// Driver Code
$arr = array(3, 1, 5, 9, 12);
$n = count($arr);

// Function call
if (findPartiion($arr, $n) == true)
    echo "Can be divided into two subsets of equal sum";
else
    echo "Can not be divided into two subsets of equal sum";

// This code is contributed by rathbhupendra
?>

Javascript

<script>
// A recursive Javascript solution for partition problem

    // A utility function that returns true if there is a
    // subset of arr[] with sum equal to given sum
    function isSubsetSum(arr,n,sum)
    {
        // Base Cases
        if (sum == 0)
            return true;
        if (n == 0 && sum != 0)
            return false;

        // If last element is greater than sum, then ignore
        // it
        if (arr[n - 1] > sum)
            return isSubsetSum(arr, n - 1, sum);

        /* else, check if sum can be obtained by any of
           the following
        (a) including the last element
        (b) excluding the last element
        */
        return isSubsetSum(arr, n - 1, sum)
            || isSubsetSum(arr, n - 1, sum - arr[n - 1]);
    }

    // Returns true if arr[] can be partitioned in two
    // subsets of equal sum, otherwise false
    function findPartition(arr,n)
    {
        // Calculate sum of the elements in array
        let sum = 0;
        for (let i = 0; i < n; i++)
            sum += arr[i];

        // If sum is odd, there cannot be two subsets
        // with equal sum
        if (sum % 2 != 0)
            return false;

        // Find if there is subset with sum equal to half
        // of total sum
        return isSubsetSum(arr, n, Math.floor(sum / 2));
    }

    // Driver code
    let arr=[3, 1, 5, 9, 12 ];
    let n = arr.length;
    // Function call
    if (findPartition(arr, n) == true)
        document.write("Can be divided into two "
                               + "subsets of equal sum");
    else
        document.write(
                "Can not be divided into "
                + "two subsets of equal sum");

    // This code is contributed by unknown2108
</script>

Output

Can be divided into two subsets of equal sum

Time Complexity: O(2^N) In the worst case, this solution tries two possibilities (whether to include or exclude) for every element.
Auxiliary Space: O(N). Recursion stack space

Partition problem using memoization:

To solve the problem follow the below idea:

As the above recursive solution has overlapping subproblems so we can declare a 2-D array to save the values for different states of the recursive function instead of solving them more than once

Follow the below steps to solve the problem:

• Declare a 2-D array of size N+1 X sum+1
• Call the recursive function with parameters as input array, size, sum, and dp array
• In this recursive function
  • If the sum is equal to zero then return true (Base case)
  • If n is equal to 0 and sum is not equal to zero then return false (Base case)
  • If the value of this subproblem is already calculated then return the answer from dp array
  • Else calculate the answer for this subproblem using the recursive formula in the above approach and save the answer in the dp array
  • Return the answer as true or false
• Print the answer

Below is the implementation of the above approach:

C++

// A recursive C++ program for partition problem
#include <bits/stdc++.h>
using namespace std;

// A utility function that returns true if there is
// a subset of arr[] with sun equal to given sum
bool isSubsetSum(int arr[], int n, int sum,
                 vector<vector<int> >& dp)
{
    // Base Cases
    if (sum == 0)
        return true;
    if (n == 0 && sum != 0)
        return false;

    // return solved subproblem
    if (dp[n][sum] != -1) {
        return dp[n][sum];
    }

    // If last element is greater than sum, then
    // ignore it
    if (arr[n - 1] > sum)
        return isSubsetSum(arr, n - 1, sum, dp);

    /* else, check if sum can be obtained by any of
        the following
        (a) including the last element
        (b) excluding the last element
    */
    // also store the subproblem in dp matrix
    return dp[n][sum]
           = isSubsetSum(arr, n - 1, sum, dp)
             || isSubsetSum(arr, n - 1, sum - arr[n - 1],
                            dp);
}

// Returns true if arr[] can be partitioned in two
// subsets of equal sum, otherwise false
bool findPartiion(int arr[], int n)
{
    // Calculate sum of the elements in array
    int sum = 0;
    for (int i = 0; i < n; i++)
        sum += arr[i];

    // If sum is odd, there cannot be two subsets
    // with equal sum
    if (sum % 2 != 0)
        return false;

    // To store overlapping subproblems
    vector<vector<int> > dp(n + 1,
                            vector<int>(sum + 1, -1));

    // Find if there is subset with sum equal to
    // half of total sum
    return isSubsetSum(arr, n, sum / 2, dp);
}

// Driver code
int main()
{
    int arr[] = { 3, 1, 5, 9, 12 };
    int n = sizeof(arr) / sizeof(arr[0]);

    // Function call
    if (findPartiion(arr, n) == true)
        cout << "Can be divided into two subsets "
                "of equal sum";
    else
        cout << "Can not be divided into two subsets"
                " of equal sum";

    int arr2[] = { 3, 1, 5, 9, 14 };
    int n2 = sizeof(arr2) / sizeof(arr2[0]);

    if (findPartiion(arr2, n2) == true)
        cout << endl
             << "Can be divided into two subsets "
                "of equal sum";
    else
        cout << endl
             << "Can not be divided into two subsets"
                " of equal sum";
    return 0;
}

Java

// Java program for partition problem
import java.io.*;
import java.util.*;

class GFG {

    // A utility function that returns true if there is
    // a subset of arr[] with sum equal to given sum
    static int isSubsetSum(int arr[], int n, int sum,
                           int[][] dp)
    {
        // Base Cases
        if (sum == 0)
            return 1;
        if (n == 0 && sum != 0)
            return 0;

        // return solved subproblem
        if (dp[n][sum] != -1) {
            return dp[n][sum];
        }

        // If last element is greater than sum, then
        // ignore it
        if (arr[n - 1] > sum)
            return isSubsetSum(arr, n - 1, sum, dp);

        /* else, check if sum can be obtained by any of
                the following
                (a) including the last element
                (b) excluding the last element
        */
        // also store the subproblem in dp matrix
        if (isSubsetSum(arr, n - 1, sum, dp) != 0
            || isSubsetSum(arr, n - 1, sum - arr[n - 1], dp)
                   != 0)
            return dp[n][sum] = 1;
        return dp[n][sum] = 0;
        // return dp[n][sum] = isSubsetSum(arr, n - 1, sum,
        // dp) || isSubsetSum(arr, n - 1, sum - arr[n - 1],
        // dp);
    }

    // Returns true if arr[] can be partitioned in two
    // subsets of equal sum, otherwise false
    static int findPartiion(int arr[], int n)
    {
        // Calculate sum of the elements in array
        int sum = 0;
        for (int i = 0; i < n; i++)
            sum += arr[i];

        // If sum is odd, there cannot be two subsets
        // with equal sum
        if (sum % 2 != 0)
            return 0;

        // To store overlapping subproblems
        int dp[][] = new int[n + 1][sum + 1];
        for (int row[] : dp)
            Arrays.fill(row, -1);

        // Find if there is subset with sum equal to
        // half of total sum
        return isSubsetSum(arr, n, sum / 2, dp);
    }

    public static void main(String[] args)
    {
        int arr[] = { 3, 1, 5, 9, 12 };
        int n = arr.length;

        // Function call
        if (findPartiion(arr, n) == 1)
            System.out.println(
                "Can be divided into two subsets of equal sum");
        else
            System.out.println(
                "Can not be divided into two subsets of equal sum");

        int arr2[] = { 3, 1, 5, 9, 14 };
        int n2 = arr2.length;

        if (findPartiion(arr2, n2) == 1)
            System.out.println(
                "Can be divided into two subsets of equal sum");
        else
            System.out.println(
                "Can not be divided into two subsets of equal sum");
    }
}

Python3

# A recursive JavaScript program for partition problem

# A utility function that returns true if there is
# a subset of arr[] with sun equal to given sum


def isSubsetSum(arr, n, sum, dp):

    # Base Cases
    if (sum == 0):
        return True
    if (n == 0 and sum != 0):
        return False

    # return solved subproblem
    if (dp[n][sum] != -1):
        return dp[n][sum]

    # If last element is greater than sum, then
    # ignore it
    if (arr[n - 1] > sum):
        return isSubsetSum(arr, n - 1, sum, dp)

        # else, check if sum can be obtained by any of
        # the following
        # (a) including the last element
        # (b) excluding the last element

    # also store the subproblem in dp matrix
    dp[n][sum] = isSubsetSum(
        arr, n - 1, sum, dp) or isSubsetSum(arr, n - 1, sum - arr[n - 1], dp)

    return dp[n][sum]

# Returns true if arr[] can be partitioned in two
# subsets of equal sum, otherwise false


def findPartiion(arr, n):

    # Calculate sum of the elements in array
    sum = 0
    for i in range(n):
        sum += arr[i]

    # If sum is odd, there cannot be two subsets
    # with equal sum
    if (sum % 2 != 0):
        return False

    # To store overlapping subproblems
    dp = [[-1]*(sum+1) for i in range(n+1)]

    # Find if there is subset with sum equal to
    # half of total sum
    return isSubsetSum(arr, n, sum // 2, dp)

# Driver code


arr = [3, 1, 5, 9, 12]
n = len(arr)

# Function call
if (findPartiion(arr, n) == True):
    print("Can be divided into two subsets of equal sum")
else:
    print("Can not be divided into two subsets of equal sum")

arr2 = [3, 1, 5, 9, 14]
n2 = len(arr2)

if (findPartiion(arr2, n2) == True):
    print("Can be divided into two subsets of equal sum")
else:
    print("Can not be divided into two subsets of equal sum")

# This code is contributed by shinjanpatra.

C#

// C# program for partition problem
using System;
public class GFG {

    // A utility function that returns true if there is
    // a subset of arr[] with sum equal to given sum
    static int isSubsetSum(int[] arr, int n, int sum,
                           int[, ] dp)
    {

        // Base Cases
        if (sum == 0)
            return 1;
        if (n == 0 && sum != 0)
            return 0;

        // return solved subproblem
        if (dp[n, sum] != -1) {
            return dp[n, sum];
        }

        // If last element is greater than sum, then
        // ignore it
        if (arr[n - 1] > sum)
            return isSubsetSum(arr, n - 1, sum, dp);

        /* else, check if sum can be obtained by any of
                    the following
                    (a) including the last element
                    (b) excluding the last element
            */
        // also store the subproblem in dp matrix
        if (isSubsetSum(arr, n - 1, sum, dp) != 0
            || isSubsetSum(arr, n - 1, sum - arr[n - 1], dp)
                   != 0)
            return dp[n, sum] = 1;
        return dp[n, sum] = 0;
        // return dp[n][sum] = isSubsetSum(arr, n - 1, sum,
        // dp) || isSubsetSum(arr, n - 1, sum - arr[n - 1],
        // dp);
    }

    // Returns true if arr[] can be partitioned in two
    // subsets of equal sum, otherwise false
    static int findPartiion(int[] arr, int n)
    {
        // Calculate sum of the elements in array
        int sum = 0;
        for (int i = 0; i < n; i++)
            sum += arr[i];

        // If sum is odd, there cannot be two subsets
        // with equal sum
        if (sum % 2 != 0)
            return 0;

        // To store overlapping subproblems
        int[, ] dp = new int[n + 1, sum + 1];

        for (int i = 0; i <= n; i++) {
            for (int j = 0; j <= sum; ++j) {
                dp[i, j] = -1;
            }
        }

        // Find if there is subset with sum equal to
        // half of total sum
        return isSubsetSum(arr, n, sum / 2, dp);
    }

    static public void Main()
    {

        // Code
        int[] arr = { 3, 1, 5, 9, 12 };
        int n = arr.Length;

        // Function call
        if (findPartiion(arr, n) == 1)
            Console.WriteLine(
                "Can be divided into two subsets of equal sum");
        else
            Console.WriteLine(
                "Can not be divided into two subsets of equal sum");

        int[] arr2 = { 3, 1, 5, 9, 14 };
        int n2 = arr2.Length;

        if (findPartiion(arr2, n2) == 1)
            Console.WriteLine(
                "Can be divided into two subsets of equal sum");
        else
            Console.WriteLine(
                "Can not be divided into two subsets of equal sum");
    }
}

// This code is contributed by lokeshmvs21.

Javascript

<script>

// A recursive JavaScript program for partition problem

// A utility function that returns true if there is
// a subset of arr[] with sun equal to given sum
function isSubsetSum(arr,n,sum,dp)
{
    // Base Cases
    if (sum == 0)
        return true;
    if (n == 0 && sum != 0)
        return false;

    // return solved subproblem
    if (dp[n][sum] != -1) {
        return dp[n][sum];
    }

    // If last element is greater than sum, then
    // ignore it
    if (arr[n - 1] > sum)
        return isSubsetSum(arr, n - 1, sum, dp);

    /* else, check if sum can be obtained by any of
        the following
        (a) including the last element
        (b) excluding the last element
    */
    // also store the subproblem in dp matrix
    return dp[n][sum]
           = isSubsetSum(arr, n - 1, sum, dp)
             || isSubsetSum(arr, n - 1, sum - arr[n - 1],
                            dp);
}

// Returns true if arr[] can be partitioned in two
// subsets of equal sum, otherwise false
function findPartiion(arr, n)
{
    // Calculate sum of the elements in array
    let sum = 0;
    for (let i = 0; i < n; i++)
        sum += arr[i];

    // If sum is odd, there cannot be two subsets
    // with equal sum
    if (sum % 2 != 0)
        return false;

    // To store overlapping subproblems
    let dp = new Array(n + 1).fill(new Array(sum+1).fill(-1));

    // Find if there is subset with sum equal to
    // half of total sum
    return isSubsetSum(arr, n, sum / 2, dp);
}

// Driver code
let arr = [ 3, 1, 5, 9, 12 ];
let n = arr.length;

    // Function call
if (findPartiion(arr, n) == true)
        document.write("Can be divided into two subsets of equal sum");
else document.write("Can not be divided into two subsets of equal sum");

let arr2 = [ 3, 1, 5, 9, 14 ];
let n2 = arr2.length;

if (findPartiion(arr2, n2) == true)
    document.write("</br>","Can be divided into two subsets of equal sum");
else document.write("</br>","Can not be divided into two subsets of equal sum");

    // This code is contributed by shinjanpatra.
</script>

Output

Can be divided into two subsets of equal sum
Can not be divided into two subsets of equal sum

Time Complexity: O(sum * N) 
Auxiliary Space: O(sum * N)

Partition problem using dynamic programming:

To solve the problem follow the below idea:

The problem can be solved using dynamic programming when the sum of the elements is not too big. As the recomputations of the same subproblems can be avoided by constructing a temporary array part[][] in a bottom-up manner using the above recursive formula and it should satisfy the following formula:

part[i][j] = true if a subset of {arr[0], arr[1], ..arr[j-1]} has sum equal to i, otherwise false

Follow the below steps to solve the problem:

• First, check if the sum of the elements is even or not
• Declare a 2-D array part[][] of size (sum/2)+1 * (N + 1)
• Run a for loop for 0 <= i <= n and set part[0][i] equal to true as zero-sum is always possible
• Run a for loop for 1 <= i <= sum/2 and set part[i][0] equal to zero as any sum with zero elements is never possible
• Run a nested for loop for 1 <= i <= sum/2 and 1 <= j <= N
  • Set part[i][j] equal to part[i][j-1]
  • If i is greater than or equal to arr[j-1], if part[i – arr[j-1]][j-1] is true then set part[i][j] as true
• Print the answer

Below is the implementation of the above approach:

C++

// A Dynamic Programming based
// C++ program to partition problem
#include <bits/stdc++.h>
using namespace std;

// Returns true if arr[] can be partitioned
// in two subsets of equal sum, otherwise false
bool findPartiion(int arr[], int n)
{
    int sum = 0;
    int i, j;

    // Calculate sum of all elements
    for (i = 0; i < n; i++)
        sum += arr[i];

    if (sum % 2 != 0)
        return false;

    bool part[sum / 2 + 1][n + 1];

    // initialize top row as true
    for (i = 0; i <= n; i++)
        part[0][i] = true;

    // initialize leftmost column,
    // except part[0][0], as 0
    for (i = 1; i <= sum / 2; i++)
        part[i][0] = false;

    // Fill the partition table in bottom up manner
    for (i = 1; i <= sum / 2; i++) {
        for (j = 1; j <= n; j++) {
            part[i][j] = part[i][j - 1];
            if (i >= arr[j - 1])
                part[i][j] = part[i][j]
                             || part[i - arr[j - 1]][j - 1];
        }
    }

    /* // uncomment this part to print table
    for (i = 0; i <= sum/2; i++)
    {
    for (j = 0; j <= n; j++)
        cout<<part[i][j];
    cout<<endl;
    } */

    return part[sum / 2][n];
}

// Driver Code
int main()
{
    int arr[] = { 3, 1, 1, 2, 2, 1 };
    int n = sizeof(arr) / sizeof(arr[0]);

    // Function call
    if (findPartiion(arr, n) == true)
        cout << "Can be divided into two subsets of equal "
                "sum";
    else
        cout << "Can not be divided into"
             << " two subsets of equal sum";
    return 0;
}

C

// A Dynamic Programming based C program to partition
// problem
#include <stdio.h>
#include <stdbool.h>

// Returns true if arr[] can be partitioned in two subsets
// of equal sum, otherwise false
bool findPartiion(int arr[], int n)
{
    int sum = 0;
    int i, j;

    // Calculate sum of all elements
    for (i = 0; i < n; i++)
        sum += arr[i];

    if (sum % 2 != 0)
        return false;

    bool part[sum / 2 + 1][n + 1];

    // initialize top row as true
    for (i = 0; i <= n; i++)
        part[0][i] = true;

    // initialize leftmost column, except part[0][0], as 0
    for (i = 1; i <= sum / 2; i++)
        part[i][0] = false;

    // Fill the partition table in bottom up manner
    for (i = 1; i <= sum / 2; i++) {
        for (j = 1; j <= n; j++) {
            part[i][j] = part[i][j - 1];
            if (i >= arr[j - 1])
                part[i][j] = part[i][j]
                             || part[i - arr[j - 1]][j - 1];
        }
    }

    /* // uncomment this part to print table
     for (i = 0; i <= sum/2; i++)
     {
       for (j = 0; j <= n; j++)
          printf ("%4d", part[i][j]);
       printf("\n");
     } */

    return part[sum / 2][n];
}

// Driver code
int main()
{
    int arr[] = { 3, 1, 1, 2, 2, 1 };
    int n = sizeof(arr) / sizeof(arr[0]);

    // Function call
    if (findPartiion(arr, n) == true)
        printf(
            "Can be divided into two subsets of equal sum");
    else
        printf("Can not be divided into two subsets of "
               "equal sum");
    getchar();
    return 0;
}

Java

// A dynamic programming based Java program for partition
// problem
import java.io.*;

class Partition {

    // Returns true if arr[] can be partitioned in two
    // subsets of equal sum, otherwise false
    static boolean findPartition(int arr[], int n)
    {
        int sum = 0;
        int i, j;

        // Calculate sum of all elements
        for (i = 0; i < n; i++)
            sum += arr[i];

        if (sum % 2 != 0)
            return false;

        boolean part[][] = new boolean[sum / 2 + 1][n + 1];

        // initialize top row as true
        for (i = 0; i <= n; i++)
            part[0][i] = true;

        // initialize leftmost column, except part[0][0], as
        // 0
        for (i = 1; i <= sum / 2; i++)
            part[i][0] = false;

        // Fill the partition table in bottom up manner
        for (i = 1; i <= sum / 2; i++) {
            for (j = 1; j <= n; j++) {
                part[i][j] = part[i][j - 1];
                if (i >= arr[j - 1])
                    part[i][j]
                        = part[i][j]
                          || part[i - arr[j - 1]][j - 1];
            }
        }

        /* // uncomment this part to print table
        for (i = 0; i <= sum/2; i++)
        {
            for (j = 0; j <= n; j++)
                printf ("%4d", part[i][j]);
            printf("\n");
        } */

        return part[sum / 2][n];
    }

    // Driver code
    public static void main(String[] args)
    {
        int arr[] = { 3, 1, 1, 2, 2, 1 };
        int n = arr.length;
        if (findPartition(arr, n) == true)
            System.out.println(
                "Can be divided into two subsets of equal sum");
        else
            System.out.println(
                "Can not be divided into two subsets of equal sum");
    }
}
/* This code is contributed by Devesh Agrawal */

Python3

# Dynamic Programming based python
# program to partition problem

# Returns true if arr[] can be
# partitioned in two subsets of
# equal sum, otherwise false


def findPartition(arr, n):
    sum = 0
    i, j = 0, 0

    # calculate sum of all elements
    for i in range(n):
        sum += arr[i]

    if sum % 2 != 0:
        return false

    part = [[True for i in range(n + 1)]
            for j in range(sum // 2 + 1)]

    # initialize top row as true
    for i in range(0, n + 1):
        part[0][i] = True

    # initialize leftmost column,
    # except part[0][0], as 0
    for i in range(1, sum // 2 + 1):
        part[i][0] = False

    # fill the partition table in
    # bottom up manner
    for i in range(1, sum // 2 + 1):

        for j in range(1, n + 1):
            part[i][j] = part[i][j - 1]

            if i >= arr[j - 1]:
                part[i][j] = (part[i][j] or
                              part[i - arr[j - 1]][j - 1])

    return part[sum // 2][n]


# Driver Code
arr = [3, 1, 1, 2, 2, 1]
n = len(arr)

# Function call
if findPartition(arr, n) == True:
    print("Can be divided into two",
          "subsets of equal sum")
else:
    print("Can not be divided into ",
          "two subsets of equal sum")

# This code is contributed
# by mohit kumar 29

C#

// A dynamic programming based C# program
// for partition problem
using System;

class GFG {

    // Returns true if arr[] can be partitioned
    // in two subsets of equal sum, otherwise
    // false
    static bool findPartition(int[] arr, int n)
    {

        int sum = 0;
        int i, j;

        // Calculate sum of all elements
        for (i = 0; i < n; i++)
            sum += arr[i];

        if (sum % 2 != 0)
            return false;

        bool[, ] part = new bool[sum / 2 + 1, n + 1];

        // initialize top row as true
        for (i = 0; i <= n; i++)
            part[0, i] = true;

        // initialize leftmost column, except
        // part[0][0], as 0
        for (i = 1; i <= sum / 2; i++)
            part[i, 0] = false;

        // Fill the partition table in bottom
        // up manner
        for (i = 1; i <= sum / 2; i++) {
            for (j = 1; j <= n; j++) {
                part[i, j] = part[i, j - 1];
                if (i >= arr[j - 1])
                    part[i, j]
                        = part[i, j - 1]
                          || part[i - arr[j - 1], j - 1];
            }
        }

        /* // uncomment this part to print table
        for (i = 0; i <= sum/2; i++)
        {
            for (j = 0; j <= n; j++)
                printf ("%4d", part[i][j]);
            printf("\n");
        } */

        return part[sum / 2, n];
    }

    // Driver code
    public static void Main()
    {
        int[] arr = { 3, 1, 1, 2, 2, 1 };
        int n = arr.Length;

        // Function call
        if (findPartition(arr, n) == true)
            Console.Write("Can be divided"
                          + " into two subsets of"
                          + " equal sum");
        else
            Console.Write("Can not be "
                          + "divided into two subsets"
                          + " of equal sum");
    }
}

// This code is contributed by Sam007.

Javascript

<script>

// A dynamic programming based javascript
// program for partition
// problemclass Partition

    // Returns true if arr can be partitioned in two
    // subsets of equal sum, otherwise false
    function findPartition(arr , n)
    {
        var sum = 0;
        var i, j;

        // Calculate sum of all elements
        for (i = 0; i < n; i++)
            sum += arr[i];

        if (sum % 2 != 0)
            return false;

        var part = Array(parseInt(sum / 2) + 1).
        fill().map(()=>Array(n + 1).fill(0));

        // initialize top row as true
        for (i = 0; i <= n; i++)
            part[0][i] = true;

        // initialize leftmost column,
        // except part[0][0], as
        // 0
        for (i = 1; i <= parseInt(sum / 2); i++)
            part[i][0] = false;

        // Fill the partition table in bottom up manner
        for (i = 1; i <= parseInt(sum / 2); i++) {
            for (j = 1; j <= n; j++) {
                part[i][j] = part[i][j - 1];
                if (i >= arr[j - 1])
                    part[i][j] = part[i][j] ||
                    part[i - arr[j - 1]][j - 1];
            }
        }

        /*
         uncomment this part to print table
         for (i = 0; i <= sum/2; i++)
         { for (j = 0; j <= n; j++)
         printf ("%4d", part[i][j]); printf("\n"); }
         */

        return part[parseInt(sum / 2)][n];
    }

    // Driver code

        var arr = [ 3, 1, 1, 2, 2, 1 ];
        var n = arr.length;
        if (findPartition(arr, n) == true)
            document.write(
            "Can be divided into two subsets of equal sum"
            );
        else
            document.write(
            "Can not be divided into two subsets of equal sum"
            );

// This code contributed by Rajput-Ji

</script>

Output

Can be divided into two subsets of equal sum

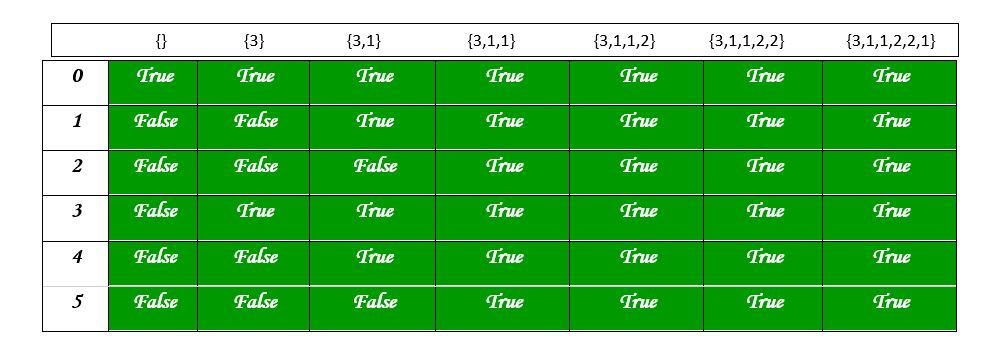
The following diagram shows the values in the partition table:

Time Complexity: O(sum * N) 
Auxiliary Space: O(sum * N) 

Note: this solution will not be feasible for arrays with a big sum

Space-optimized approach for the above solution:

To solve the problem follow the below idea:

We can space optimize the above dp approach as for calculating the values of the current row we require only previous row

Below is the implementation of the above approach: 

C++

// A Dynamic Programming based
// C++ program to partition problem
#include <bits/stdc++.h>
using namespace std;

// Returns true if arr[] can be partitioned
// in two subsets of equal sum, otherwise false
bool findPartiion(int arr[], int n)
{
    int sum = 0;
    int i, j;

    // Calculate sum of all elements
    for (i = 0; i < n; i++)
        sum += arr[i];

    if (sum % 2 != 0)
        return false;

    bool part[sum / 2 + 1];

    // Initialize the part array
    // as 0
    for (i = 0; i <= sum / 2; i++) {
        part[i] = 0;
    }

    // Fill the partition table in bottom up manner

    for (i = 0; i < n; i++) {
        // the element to be included
        // in the sum cannot be
        // greater than the sum
        for (j = sum / 2; j >= arr[i];
             j--) { // check if sum - arr[i]
            // could be formed
            // from a subset
            // using elements
            // before index i
            if (part[j - arr[i]] == 1 || j == arr[i])
                part[j] = 1;
        }
    }

    return part[sum / 2];
}

// Driver Code
int main()
{
    int arr[] = { 1, 3, 3, 2, 3, 2 };
    int n = sizeof(arr) / sizeof(arr[0]);

    // Function call
    if (findPartiion(arr, n) == true)
        cout << "Can be divided into two subsets of equal "
                "sum";
    else
        cout << "Can not be divided into"
             << " two subsets of equal sum";
    return 0;
}

Java

// A Dynamic Programming based
// Java program to partition problem
import java.io.*;

class GFG {

    // Returns true if arr[] can be partitioned
    // in two subsets of equal sum, otherwise false
    public static boolean findPartiion(int arr[], int n)
    {
        int sum = 0;
        int i, j;

        // Calculate sum of all elements
        for (i = 0; i < n; i++)
            sum += arr[i];

        if (sum % 2 != 0)
            return false;

        boolean[] part = new boolean[sum / 2 + 1];

        // Initialize the part array
        // as 0
        for (i = 0; i <= sum / 2; i++) {
            part[i] = false;
        }

        // Fill the partition table in
        // bottom up manner
        for (i = 0; i < n; i++) {

            // The element to be included
            // in the sum cannot be
            // greater than the sum
            for (j = sum / 2; j >= arr[i]; j--) {

                // Check if sum - arr[i] could be
                // formed from a subset using elements
                // before index i
                if (part[j - arr[i]] == true || j == arr[i])
                    part[j] = true;
            }
        }
        return part[sum / 2];
    }

    // Driver code
    public static void main(String[] args)
    {
        int arr[] = { 1, 3, 3, 2, 3, 2 };
        int n = 6;

        // Function call
        if (findPartiion(arr, n) == true)
            System.out.println("Can be divided into two "
                               + "subsets of equal sum");
        else
            System.out.println(
                "Can not be divided into "
                + "two subsets of equal sum");
    }
}

// This code is contributed by RohitOberoi

Python3

# A Dynamic Programming based
# Python3 program to partition problem

# Returns true if arr[] can be partitioned
# in two subsets of equal sum, otherwise false


def findPartiion(arr, n):
    Sum = 0

    # Calculate sum of all elements
    for i in range(n):
        Sum += arr[i]
    if (Sum % 2 != 0):
        return 0
    part = [0] * ((Sum // 2) + 1)

    # Initialize the part array as 0
    for i in range((Sum // 2) + 1):
        part[i] = 0

    # Fill the partition table in bottom up manner
    for i in range(n):

        # the element to be included
        # in the sum cannot be
        # greater than the sum
        for j in range(Sum // 2, arr[i] - 1, -1):

            # check if sum - arr[i]
            # could be formed
            # from a subset
            # using elements
            # before index i
            if (part[j - arr[i]] == 1 or j == arr[i]):
                part[j] = 1

    return part[Sum // 2]


# Driver code
arr = [1, 3, 3, 2, 3, 2]
n = len(arr)

# Function call
if (findPartiion(arr, n) == 1):
    print("Can be divided into two subsets of equal sum")
else:
    print("Can not be divided into two subsets of equal sum")

    # This code is contributed by divyeshrabadiya07

C#

// A Dynamic Programming based
// C# program to partition problem
using System;
class GFG {

    // Returns true if arr[] can be partitioned
    // in two subsets of equal sum, otherwise false
    static bool findPartiion(int[] arr, int n)
    {
        int sum = 0;
        int i, j;

        // Calculate sum of all elements
        for (i = 0; i < n; i++)
            sum += arr[i];
        if (sum % 2 != 0)
            return false;
        bool[] part = new bool[sum / 2 + 1];

        // Initialize the part array
        // as 0
        for (i = 0; i <= sum / 2; i++) {
            part[i] = false;
        }

        // Fill the partition table in
        // bottom up manner
        for (i = 0; i < n; i++) {

            // The element to be included
            // in the sum cannot be
            // greater than the sum
            for (j = sum / 2; j >= arr[i]; j--) {

                // Check if sum - arr[i] could be
                // formed from a subset using elements
                // before index i
                if (part[j - arr[i]] == true || j == arr[i])
                    part[j] = true;
            }
        }
        return part[sum / 2];
    }

    // Driver code
    static void Main()
    {
        int[] arr = { 1, 3, 3, 2, 3, 2 };
        int n = 6;

        // Function call
        if (findPartiion(arr, n) == true)
            Console.WriteLine("Can be divided into two "
                              + "subsets of equal sum");
        else
            Console.WriteLine("Can not be divided into "
                              + "two subsets of equal sum");
    }
}

// This code is contributed by divyesh072019

Javascript

<script>

// A Dynamic Programming based Javascript
// program to partition problem

// Returns true if arr[] can be partitioned
// in two subsets of equal sum, otherwise false
function findPartiion(arr, n)
{
    let sum = 0;
    let i, j;

    // Calculate sum of all elements
    for(i = 0; i < n; i++)
        sum += arr[i];

    if (sum % 2 != 0)
        return false;

    let part = new Array(parseInt(sum / 2 + 1, 10));

    // Initialize the part array
    // as 0
    for(i = 0; i <= parseInt(sum / 2, 10); i++)
    {
        part[i] = false;
    }

    // Fill the partition table in
    // bottom up manner
    for(i = 0; i < n; i++)
    {

        // The element to be included
        // in the sum cannot be
        // greater than the sum
        for(j = parseInt(sum / 2, 10);
            j >= arr[i];
            j--)
        {
            // Check if sum - arr[i] could be
            // formed from a subset using
            // elements before index i
            if (part[j - arr[i]] == true ||
                    j == arr[i])
                part[j] = true;
        }
    }
    return part[parseInt(sum / 2, 10)];
}

// Driver code
let arr = [ 1, 3, 3, 2, 3, 2 ];
let n = arr.length;

// Function call
if (findPartiion(arr, n) == true)
    document.write("Can be divided into two " +
                   "subsets of equal sum");
else
    document.write("Can not be divided into " +
                   "two subsets of equal sum");

// This code is contributed by suresh07

</script>

Output

Can be divided into two subsets of equal sum

Time Complexity: O(sum * N)
Auxiliary Space: O(sum)

Please write comments if you find anything incorrect, or if you want to share more information about the topic discussed above.