Sum over Subsets | Dynamic Programming
Last Updated :
29 Mar, 2024
Prerequisite: Basic Dynamic Programming, Bitmasks
Consider the following problem where we will use Sum over subset Dynamic Programming to solve it.
Given an array of 2n integers, we need to calculate function F(x) = ?Ai such that x&i==i for all x. i.e, i is a bitwise subset of x. i will be a bitwise subset of mask x, if x&i==i.
Examples:
Input: A[] = {7, 12, 14, 16} , n = 2
Output: 7, 19, 21, 49
Explanation: There will be 4 values of x: 0,1,2,3
So, we need to calculate F(0),F(1),F(2),F(3).
Now, F(0) = A0 = 7
F(1) = A0 + A1 = 19
F(2) = A0 + A2 = 21
F(3) = A0 + A1 + A2 + A3 = 49
Input: A[] = {7, 11, 13, 16} , n = 2
Output: 7, 18, 20, 47
Explanation: There will be 4 values of x: 0,1,2,3
So, we need to calculate F(0),F(1),F(2),F(3).
Now, F(0) = A0 = 7
F(1) = A0 + A1 = 18
F(2) = A0 + A2 = 20
F(3) = A0 + A1 + A2 + A3 = 47
Brute-Force Approach:
Iterate for all the x from 0 to (2n-1) . Calculate the bitwise subsets of all the x and sum it up for every x.
Time-Complexity: O(4^n)
Below is the implementation of above idea:
C++
#include <bits/stdc++.h>
using namespace std;
void SumOverSubsets(int a[], int n) {
int sos[1 << n] = {0};
for (int x = 0; x < (1 << n); x++) {
for (int i = 0; i < (1 << n); i++) {
if ((x & i) == i)
sos[x] += a[i];
}
}
for (int i = 0; i < (1 << n); i++)
cout << sos[i] << " ";
}
int main() {
int a[] = {7, 12, 14, 16};
int n = 2;
SumOverSubsets(a, n);
return 0;
}
|
Java
class GFG{
static void SumOverSubsets(int a[], int n) {
int sos[] = new int [1 << n];
for (int x = 0; x < (1 << n); x++) {
for (int i = 0; i < (1 << n); i++) {
if ((x & i) == i)
sos[x] += a[i];
}
}
for (int i = 0; i < (1 << n); i++)
System.out.printf("%d ", sos[i]);
}
public static void main(String[] args) {
int a[] = {7, 12, 14, 16};
int n = 2;
SumOverSubsets(a, n);
}
}
|
Python3
def SumOverSubsets(a, n):
sos = [0] * (1 << n)
for x in range(0,(1 << n)):
for i in range(0,(1 << n)):
if ((x & i) == i):
sos[x] += a[i]
for i in range(0,(1 << n)):
print(sos[i],end = " ")
a = [7, 12, 14, 16]
n = 2
SumOverSubsets(a, n)
|
C#
using System;
class GFG {
static void SumOverSubsets(int []a, int n)
{
int []sos = new int [1 << n];
for (int x = 0; x < (1 << n); x++)
{
for (int i = 0; i < (1 << n); i++)
{
if ((x & i) == i)
sos[x] += a[i];
}
}
for (int i = 0; i < (1 << n); i++)
Console.Write(sos[i] + " ");
}
public static void Main()
{
int []a = {7, 12, 14, 16};
int n = 2;
SumOverSubsets(a, n);
}
}
|
PHP
<?php
function SumOverSubsets($a, $n)
{
$sos = array(1 << $n);
for($i = 0 ;$i < (1 << $n); $i++)
$sos[$i] = 0;
for ($x = 0; $x < (1 << $n); $x++)
{
for($i = 0; $i < (1 << $n); $i++)
{
if (($x & $i) == $i)
$sos[$x] += $a[$i];
}
}
for ($i = 0; $i < (1 << $n); $i++)
echo $sos[$i] . " ";
}
$a = array(7, 12, 14, 16);
$n = 2;
SumOverSubsets($a, $n);
?>
|
Javascript
<script>
function SumOverSubsets(a, n)
{
let sos = new Array(1 << n);
sos.fill(0);
for (let x = 0; x < (1 << n); x++)
{
for (let i = 0; i < (1 << n); i++)
{
if ((x & i) == i)
sos[x] += a[i];
}
}
for (let i = 0; i < (1 << n); i++)
document.write(sos[i] + " ");
}
let a = [7, 12, 14, 16];
let n = 2;
SumOverSubsets(a, n);
</script>
|
Output:
7 19 21 49
.
Sub-Optimal Approach:
The brute-force algorithm can be easily improved by just iterating over bitwise subsets. Instead of iterating for every i, we can simply iterate for the bitwise subsets only. Iterating backward for i=(i-1)&x gives us every bitwise subset, where i starts from x and ends at 1. If the mask x has k set bits, we do 2k iterations. A number of k set bits will have 2k bitwise subsets. Therefore total number of mask x with k set bits is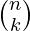 . Therefore the total number of iterations is ?
. Therefore the total number of iterations is ?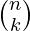 2k = 3n
2k = 3n
Time Complexity: O(3n)
Below is the implementation of above idea:
C++
#include <bits/stdc++.h>
using namespace std;
void SumOverSubsets(int a[], int n) {
int sos[1 << n] = {0};
for (int x = 0; x < (1 << n); x++) {
sos[x] = a[0];
for (int i = x; i > 0; i = (i - 1) & x)
sos[x] += a[i];
}
for (int i = 0; i < (1 << n); i++)
cout << sos[i] << " ";
}
int main() {
int a[] = {7, 12, 14, 16};
int n = 2;
SumOverSubsets(a, n);
return 0;
}
|
Java
public class GFG {
static void SumOverSubsets(int a[], int n)
{
int sos[] = new int[(1 << n)];
for (int x = 0; x < (1 << n); x++) {
sos[x] = a[0];
for (int i = x; i > 0; i = (i - 1) & x)
sos[x] += a[i];
}
for (int i = 0; i < (1 << n); i++)
System.out.print(sos[i] + " ");
}
public static void main(String args[])
{
int a[] = {7, 12, 14, 16};
int n = 2;
SumOverSubsets(a, n);
}
}
|
Python3
def SumOverSubsets(a, n):
sos = [0]*(1 << n)
for x in range((1 << n)):
sos[x] = a[0]
i = x
while i > 0:
sos[x] += a[i]
i = ((i - 1) & x)
for i in range(1<<n):
print(sos[i], end = " ")
if __name__ == '__main__':
a = [7, 12, 14, 16]
n = 2
SumOverSubsets(a, n)
|
C#
using System;
class GFG {
static void SumOverSubsets(int []a, int n)
{
int []sos = new int[(1 << n)];
for (int x = 0; x < (1 << n); x++) {
sos[x] = a[0];
for (int i = x; i > 0; i = (i - 1) & x)
sos[x] += a[i];
}
for (int i = 0; i < (1 << n); i++)
Console.Write(sos[i] + " ");
}
static void Main()
{
int []a = {7, 12, 14, 16};
int n = 2;
SumOverSubsets(a, n);
}
}
|
PHP
<?php
function SumOverSubsets($a,$n)
{
$sos=array(1 << $n);
for ($x = 0; $x < (1 << $n); $x++)
{
$sos[$x] = $a[0];
for ($i = $x; $i > 0; $i = ($i - 1) & $x)
$sos[$x] += $a[$i];
}
for ($i = 0; $i < (1 << $n); $i++)
echo $sos[$i] . " ";
}
$a = array(7, 12, 14, 16);
$n = 2;
SumOverSubsets($a, $n);
?>
|
Javascript
<script>
function SumOverSubsets(a, n)
{
let sos = new Array((1 << n));
sos.fill(0);
for (let x = 0; x < (1 << n); x++) {
sos[x] = a[0];
for (let i = x; i > 0; i = (i - 1) & x)
sos[x] += a[i];
}
for (let i = 0; i < (1 << n); i++)
document.write(sos[i] + " ");
}
let a = [7, 12, 14, 16];
let n = 2;
SumOverSubsets(a, n);
</script>
|
Output:
7 19 21 49
Time Complexity: O(n*2n)
Auxiliary Space: O(2n)
Reference:
Share your thoughts in the comments
Please Login to comment...