Longest Increasing Subsequence (LIS)
Last Updated :
27 Sep, 2023
Given an array arr[] of size N, the task is to find the length of the Longest Increasing Subsequence (LIS) i.e., the longest possible subsequence in which the elements of the subsequence are sorted in increasing order.
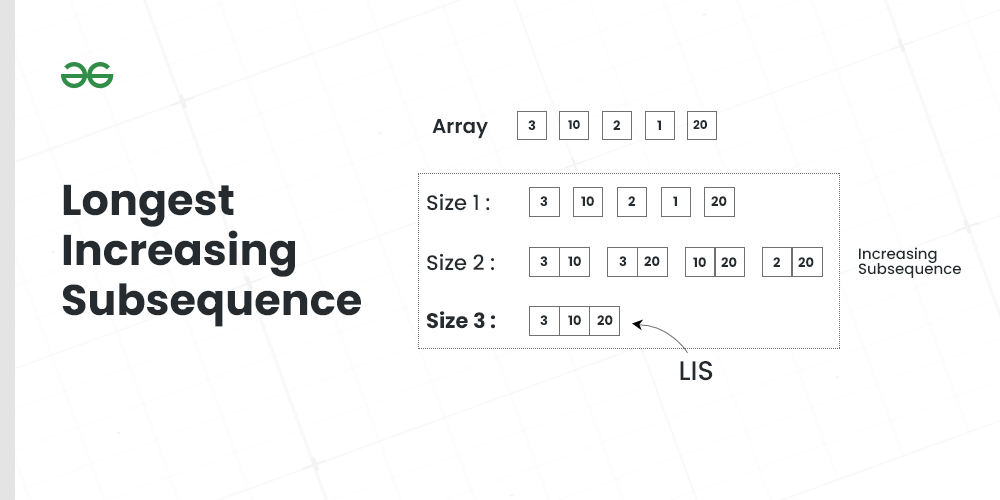
Longest Increasing Subsequence
Examples:
Input: arr[] = {3, 10, 2, 1, 20}
Output: 3
Explanation: The longest increasing subsequence is 3, 10, 20
Input: arr[] = {3, 2}
Output:1
Explanation: The longest increasing subsequences are {3} and {2}
Input: arr[] = {50, 3, 10, 7, 40, 80}
Output: 4
Explanation: The longest increasing subsequence is {3, 7, 40, 80}
Longest Increasing Sequence using Recursion:
The problem can be solved based on the following idea:
Let L(i) be the length of the LIS ending at index i such that arr[i] is the last element of the LIS. Then, L(i) can be recursively written as:
- L(i) = 1 + max(L(j) ) where 0 < j < i and arr[j] < arr[i]; or
- L(i) = 1, if no such j exists.
Formally, the length of LIS ending at index i, is 1 greater than the maximum of lengths of all LIS ending at some index j such that arr[j] < arr[i] where j < i.
We can see that the above recurrence relation follows the optimal substructure property.
Illustration:
Follow the below illustration for a better understanding:
Consider arr[] = {3, 10, 2, 11}
L(i): Denotes LIS of subarray ending at position ‘i’
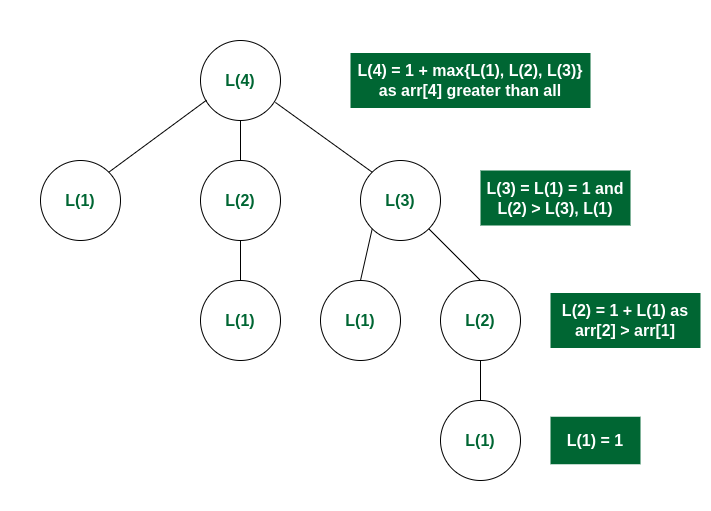
Recursion Tree
Follow the steps mentioned below to implement the above idea:
- Create a recursive function.
- For each recursive call, Iterate from the i = 1 to the current position and do the following:
- Find the possible length of the longest increasing subsequence ending at the current position if the previous sequence ended at i.
- Update the maximum possible length accordingly.
- Repeat this for all indices and find the answer
Below is the implementation of the recursive approach:
C++
#include <bits/stdc++.h>
using namespace std;
int _lis(int arr[], int n, int* max_ref)
{
if (n == 1)
return 1;
int res, max_ending_here = 1;
for (int i = 1; i < n; i++) {
res = _lis(arr, i, max_ref);
if (arr[i - 1] < arr[n - 1]
&& res + 1 > max_ending_here)
max_ending_here = res + 1;
}
if (*max_ref < max_ending_here)
*max_ref = max_ending_here;
return max_ending_here;
}
int lis(int arr[], int n)
{
int max = 1;
_lis(arr, n, &max);
return max;
}
int main()
{
int arr[] = { 10, 22, 9, 33, 21, 50, 41, 60 };
int n = sizeof(arr) / sizeof(arr[0]);
cout << "Length of lis is " << lis(arr, n);
return 0;
}
|
C
#include <stdio.h>
#include <stdlib.h>
int _lis(int arr[], int n, int* max_ref)
{
if (n == 1)
return 1;
int res, max_ending_here = 1;
for (int i = 1; i < n; i++) {
res = _lis(arr, i, max_ref);
if (arr[i - 1] < arr[n - 1]
&& res + 1 > max_ending_here)
max_ending_here = res + 1;
}
if (*max_ref < max_ending_here)
*max_ref = max_ending_here;
return max_ending_here;
}
int lis(int arr[], int n)
{
int max = 1;
_lis(arr, n, &max);
return max;
}
int main()
{
int arr[] = { 10, 22, 9, 33, 21, 50, 41, 60 };
int n = sizeof(arr) / sizeof(arr[0]);
printf("Length of lis is %d", lis(arr, n));
return 0;
}
|
Java
import java.io.*;
import java.util.*;
class LIS {
static int max_ref;
static int _lis(int arr[], int n)
{
if (n == 1)
return 1;
int res, max_ending_here = 1;
for (int i = 1; i < n; i++) {
res = _lis(arr, i);
if (arr[i - 1] < arr[n - 1]
&& res + 1 > max_ending_here)
max_ending_here = res + 1;
}
if (max_ref < max_ending_here)
max_ref = max_ending_here;
return max_ending_here;
}
static int lis(int arr[], int n)
{
max_ref = 1;
_lis(arr, n);
return max_ref;
}
public static void main(String args[])
{
int arr[] = { 10, 22, 9, 33, 21, 50, 41, 60 };
int n = arr.length;
System.out.println("Length of lis is "
+ lis(arr, n));
}
}
|
Python3
global maximum
def _lis(arr, n):
global maximum
if n == 1:
return 1
maxEndingHere = 1
for i in range(1, n):
res = _lis(arr, i)
if arr[i-1] < arr[n-1] and res+1 > maxEndingHere:
maxEndingHere = res + 1
maximum = max(maximum, maxEndingHere)
return maxEndingHere
def lis(arr):
global maximum
n = len(arr)
maximum = 1
_lis(arr, n)
return maximum
if __name__ == '__main__':
arr = [10, 22, 9, 33, 21, 50, 41, 60]
n = len(arr)
print("Length of lis is", lis(arr))
|
C#
using System;
class LIS {
static int max_ref;
static int _lis(int[] arr, int n)
{
if (n == 1)
return 1;
int res, max_ending_here = 1;
for (int i = 1; i < n; i++) {
res = _lis(arr, i);
if (arr[i - 1] < arr[n - 1]
&& res + 1 > max_ending_here)
max_ending_here = res + 1;
}
if (max_ref < max_ending_here)
max_ref = max_ending_here;
return max_ending_here;
}
static int lis(int[] arr, int n)
{
max_ref = 1;
_lis(arr, n);
return max_ref;
}
public static void Main()
{
int[] arr = { 10, 22, 9, 33, 21, 50, 41, 60 };
int n = arr.Length;
Console.Write("Length of lis is " + lis(arr, n)
+ "\n");
}
}
|
Javascript
<script>
let max_ref;
function _lis(arr,n)
{
if (n == 1)
return 1;
let res, max_ending_here = 1;
for (let i = 1; i < n; i++)
{
res = _lis(arr, i);
if (arr[i-1] < arr[n-1] && res + 1 > max_ending_here)
max_ending_here = res + 1;
}
if (max_ref < max_ending_here)
max_ref = max_ending_here;
return max_ending_here;
}
function lis(arr,n)
{
max_ref = 1;
_lis( arr, n);
return max_ref;
}
let arr=[10, 22, 9, 33, 21, 50, 41, 60 ]
let n = arr.length;
document.write("Length of lis is "
+ lis(arr, n) + "<br>");
</script>
|
Output
Length of lis is 5
Time Complexity: O(2n) The time complexity of this recursive approach is exponential as there is a case of overlapping subproblems as explained in the recursive tree diagram above.
Auxiliary Space: O(1). No external space is used for storing values apart from the internal stack space.
Longest Increasing Subsequence using Memoization:
If noticed carefully, we can see that the above recursive solution also follows the overlapping subproblems property i.e., same substructure solved again and again in different recursion call paths. We can avoid this using the memoization approach.
We can see that each state can be uniquely identified using two parameters:
- Current index (denotes the last index of the LIS) and
- Previous index (denotes the ending index of the previous LIS behind which the arr[i] is being concatenated).
Below is the implementation of the above approach.
C++
#include <bits/stdc++.h>
using namespace std;
int f(int idx, int prev_idx, int n, int a[],
vector<vector<int> >& dp)
{
if (idx == n) {
return 0;
}
if (dp[idx][prev_idx + 1] != -1) {
return dp[idx][prev_idx + 1];
}
int notTake = 0 + f(idx + 1, prev_idx, n, a, dp);
int take = INT_MIN;
if (prev_idx == -1 || a[idx] > a[prev_idx]) {
take = 1 + f(idx + 1, idx, n, a, dp);
}
return dp[idx][prev_idx + 1] = max(take, notTake);
}
int longestSubsequence(int n, int a[])
{
vector<vector<int> > dp(n + 1, vector<int>(n + 1, -1));
return f(0, -1, n, a, dp);
}
int main()
{
int a[] = { 3, 10, 2, 1, 20 };
int n = sizeof(a) / sizeof(a[0]);
cout << "Length of lis is " << longestSubsequence(n, a);
return 0;
}
|
Java
import java.lang.*;
import java.util.Arrays;
class LIS {
static int f(int idx, int prev_idx, int n, int a[],
int[][] dp)
{
if (idx == n) {
return 0;
}
if (dp[idx][prev_idx + 1] != -1) {
return dp[idx][prev_idx + 1];
}
int notTake = 0 + f(idx + 1, prev_idx, n, a, dp);
int take = Integer.MIN_VALUE;
if (prev_idx == -1 || a[idx] > a[prev_idx]) {
take = 1 + f(idx + 1, idx, n, a, dp);
}
return dp[idx][prev_idx + 1]
= Math.max(take, notTake);
}
static int lis(int arr[], int n)
{
int dp[][] = new int[n + 1][n + 1];
for (int row[] : dp)
Arrays.fill(row, -1);
return f(0, -1, n, arr, dp);
}
public static void main(String args[])
{
int a[] = { 3, 10, 2, 1, 20 };
int n = a.length;
System.out.println("Length of lis is " + lis(a, n));
}
}
|
Python3
import sys
def f(idx, prev_idx, n, a, dp):
if (idx == n):
return 0
if (dp[idx][prev_idx + 1] != -1):
return dp[idx][prev_idx + 1]
notTake = 0 + f(idx + 1, prev_idx, n, a, dp)
take = -sys.maxsize - 1
if (prev_idx == -1 or a[idx] > a[prev_idx]):
take = 1 + f(idx + 1, idx, n, a, dp)
dp[idx][prev_idx + 1] = max(take, notTake)
return dp[idx][prev_idx + 1]
def longestSubsequence(n, a):
dp = [[-1 for i in range(n + 1)]for j in range(n + 1)]
return f(0, -1, n, a, dp)
if __name__ == '__main__':
a = [3, 10, 2, 1, 20]
n = len(a)
print("Length of lis is", longestSubsequence(n, a))
|
C#
using System;
class GFG {
public static int INT_MIN = -2147483648;
public static int f(int idx, int prev_idx, int n,
int[] a, int[, ] dp)
{
if (idx == n) {
return 0;
}
if (dp[idx, prev_idx + 1] != -1) {
return dp[idx, prev_idx + 1];
}
int notTake = 0 + f(idx + 1, prev_idx, n, a, dp);
int take = INT_MIN;
if (prev_idx == -1 || a[idx] > a[prev_idx]) {
take = 1 + f(idx + 1, idx, n, a, dp);
}
return dp[idx, prev_idx + 1]
= Math.Max(take, notTake);
}
public static int longestSubsequence(int n, int[] a)
{
int[, ] dp = new int[n + 1, n + 1];
for (int i = 0; i < n + 1; i++) {
for (int j = 0; j < n + 1; j++) {
dp[i, j] = -1;
}
}
return f(0, -1, n, a, dp);
}
static void Main()
{
int[] a = { 3, 10, 2, 1, 20 };
int n = a.Length;
Console.WriteLine("Length of lis is "
+ longestSubsequence(n, a));
}
}
|
Javascript
function f(idx, prev_idx, n, a, dp) {
if (idx == n) {
return 0;
}
if (dp[idx][prev_idx + 1] != -1) {
return dp[idx][prev_idx + 1];
}
var notTake = 0 + f(idx + 1, prev_idx, n, a, dp);
var take = Number.MIN_VALUE;
if (prev_idx == -1 || a[idx] > a[prev_idx]) {
take = 1 + f(idx + 1, idx, n, a, dp);
}
return (dp[idx][prev_idx + 1] = Math.max(take, notTake));
}
function longestSubsequence(n, a) {
var dp = Array(n + 1)
.fill()
.map(() => Array(n + 1).fill(-1));
return f(0, -1, n, a, dp);
}
var a = [3, 10, 2, 1, 20];
var n = 5;
console.log("Length of lis is " + longestSubsequence(n, a));
|
Output
Length of lis is 3
Time Complexity: O(N2)
Auxiliary Space: O(N2)
Due to optimal substructure and overlapping subproblem property, we can also utilise Dynamic programming to solve the problem. Instead of memoization, we can use the nested loop to implement the recursive relation.
The outer loop will run from i = 1 to N and the inner loop will run from j = 0 to i and use the recurrence relation to solve the problem.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int lis(int arr[], int n)
{
int lis[n];
lis[0] = 1;
for (int i = 1; i < n; i++) {
lis[i] = 1;
for (int j = 0; j < i; j++)
if (arr[i] > arr[j] && lis[i] < lis[j] + 1)
lis[i] = lis[j] + 1;
}
return *max_element(lis, lis + n);
}
int main()
{
int arr[] = { 10, 22, 9, 33, 21, 50, 41, 60 };
int n = sizeof(arr) / sizeof(arr[0]);
printf("Length of lis is %d\n", lis(arr, n));
return 0;
}
|
Java
import java.lang.*;
class LIS {
static int lis(int arr[], int n)
{
int lis[] = new int[n];
int i, j, max = 0;
for (i = 0; i < n; i++)
lis[i] = 1;
for (i = 1; i < n; i++)
for (j = 0; j < i; j++)
if (arr[i] > arr[j] && lis[i] < lis[j] + 1)
lis[i] = lis[j] + 1;
for (i = 0; i < n; i++)
if (max < lis[i])
max = lis[i];
return max;
}
public static void main(String args[])
{
int arr[] = { 10, 22, 9, 33, 21, 50, 41, 60 };
int n = arr.length;
System.out.println("Length of lis is "
+ lis(arr, n));
}
}
|
Python3
def lis(arr):
n = len(arr)
lis = [1]*n
for i in range(1, n):
for j in range(0, i):
if arr[i] > arr[j] and lis[i] < lis[j] + 1:
lis[i] = lis[j]+1
maximum = 0
for i in range(n):
maximum = max(maximum, lis[i])
return maximum
if __name__ == '__main__':
arr = [10, 22, 9, 33, 21, 50, 41, 60]
print("Length of lis is", lis(arr))
|
C#
using System;
class LIS {
static int lis(int[] arr, int n)
{
int[] lis = new int[n];
int i, j, max = 0;
for (i = 0; i < n; i++)
lis[i] = 1;
for (i = 1; i < n; i++)
for (j = 0; j < i; j++)
if (arr[i] > arr[j] && lis[i] < lis[j] + 1)
lis[i] = lis[j] + 1;
for (i = 0; i < n; i++)
if (max < lis[i])
max = lis[i];
return max;
}
public static void Main()
{
int[] arr = { 10, 22, 9, 33, 21, 50, 41, 60 };
int n = arr.Length;
Console.WriteLine("Length of lis is "
+ lis(arr, n));
}
}
|
Javascript
<script>
function lis(arr, n)
{
let lis = Array(n).fill(0);
let i, j, max = 0;
for(i = 0; i < n; i++)
lis[i] = 1;
for(i = 1; i < n; i++)
for(j = 0; j < i; j++)
if (arr[i] > arr[j] && lis[i] < lis[j] + 1)
lis[i] = lis[j] + 1;
for(i = 0; i < n; i++)
if (max < lis[i])
max = lis[i];
return max;
}
let arr = [ 10, 22, 9, 33, 21, 50, 41, 60 ];
let n = arr.length;
document.write("Length of lis is " + lis(arr, n) + "\n");
</script>
|
Output
Length of lis is 5
Time Complexity: O(N2) As a nested loop is used.
Auxiliary Space: O(N) Use of any array to store LIS values at each index.
Note: The time complexity of the above Dynamic Programming (DP) solution is O(n^2), but there is an O(N* logN) solution for the LIS problem. We have not discussed the O(N log N) solution here.
Refer: Longest Increasing Subsequence Size (N * logN) for the mentioned approach.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...