Understanding Types of Means | Set 1
Last Updated :
25 Jul, 2022
It is one of the most important concepts of statistics, a crucial subject to learning Machine Learning.
- Arithmetic Mean: It is the mathematical expectation of a discrete set of numbers or averages.
Denoted by X̂, pronounced as “x-bar”. It is the sum of all the discrete values in the set divided by the total number of values in the set.
The formula to calculate the mean of n values – x1, x2, ….. xn
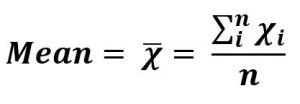
Sequence = {1, 5, 6, 4, 4}
Sum = 20
n, Total values = 5
Arithmetic Mean = 20/5 = 4
Python3
import statistics
data1 = [1, 5, 6, 4, 4]
x = statistics.mean(data1)
print("Mean is :", x)
|
Mean is : 4
- Trimmed Mean: Arithmetic Mean is influenced by the outliers (extreme values) in the data. So, trimmed mean is used at the time of pre-processing when we are handling such kinds of data in machine learning.
It is arithmetic having a variation i.e. it is calculated by dropping a fixed number of sorted values from each end of the sequence of data given and then calculating the mean (average) of the remaining values.
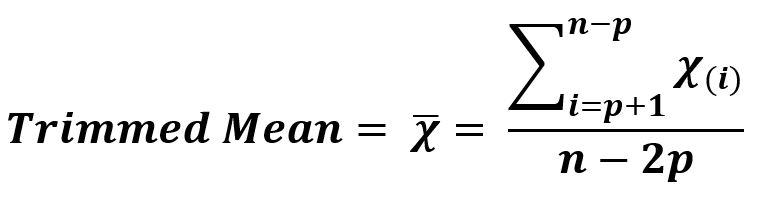
Sequence = {0, 2, 1, 3}
p = 0.25
Remaining Sequence = {2, 1}
n, Total values = 2
Mean = 3/2 = 1.5
Python3
from scipy import stats
data = [0, 2, 1, 3]
x = stats.trim_mean(data, 0.25)
print("Trimmed Mean is :", x)
|
Trimmed Mean is : 1.5
- Weighted Mean: Arithmetic Mean or Trimmed mean is giving equal importance to all the parameters involved. But whenever we are working on machine learning predictions, there is a possibility that some parameter values hold more importance than others, so we assign high weights to the values of such parameters. Also, there can be a chance that our data set has a highly variable value of a parameter, so we assign lesser weights to the values of such parameters.
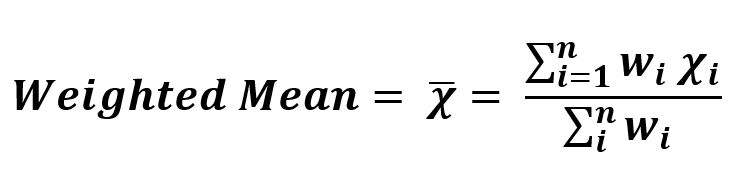
Sequence = [0, 2, 1, 3]
Weight = [1, 0, 1, 1]
Sum (Weight * sequence) = 0*1 + 2*0 + 1*1 + 3*1
Sum (Weight) = 3
Weighted Mean = 4 / 3 = 1.3333333333333333
Python3
import numpy as np
data = [0, 2, 1, 3]
x = np.average(data, weights =[1, 0, 1, 1])
print("Weighted Mean is :", x)
|
Weighted Mean is : 1.3333333333333333
Python3
data = [0, 2, 1, 3]
weights = [1, 0, 1, 1]
x = sum(data[i] * weights[i]
for i in range(len(data))) / sum(weights)
print ("Weighted Mean is :", x)
|
Weighted Mean is : 1.3333333333333333
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...