Bias and Variance in Machine Learning
Last Updated :
05 Jun, 2023
There are various ways to evaluate a machine-learning model. We can use MSE (Mean Squared Error) for Regression; Precision, Recall, and ROC (Receiver of Characteristics) for a Classification Problem along with Absolute Error. In a similar way, Bias and Variance help us in parameter tuning and deciding better-fitted models among several built.
Bias is one type of error that occurs due to wrong assumptions about data such as assuming data is linear when in reality, data follows a complex function. On the other hand, variance gets introduced with high sensitivity to variations in training data. This also is one type of error since we want to make our model robust against noise. There are two types of error in machine learning. Reducible error and Irreducible error. Bias and Variance come under reducible error.
What is Bias?
Bias is simply defined as the inability of the model because of that there is some difference or error occurring between the model’s predicted value and the actual value. These differences between actual or expected values and the predicted values are known as error or bias error or error due to bias. Bias is a systematic error that occurs due to wrong assumptions in the machine learning process.
Let 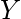 be the true value of a parameter, and let
be the true value of a parameter, and let 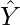 be an estimator of
be an estimator of 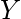 based on a sample of data. Then, the bias of the estimator
based on a sample of data. Then, the bias of the estimator 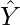 is given by:
is given by:
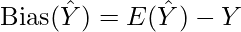
where 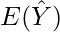 is the expected value of the estimator
is the expected value of the estimator 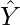 . It is the measurement of the model that how well it fits the data.
. It is the measurement of the model that how well it fits the data.
- Low Bias: Low bias value means fewer assumptions are taken to build the target function. In this case, the model will closely match the training dataset.
- High Bias: High bias value means more assumptions are taken to build the target function. In this case, the model will not match the training dataset closely.
The high-bias model will not be able to capture the dataset trend. It is considered as the underfitting model which has a high error rate. It is due to a very simplified algorithm.
For example, a linear regression model may have a high bias if the data has a non-linear relationship.
Ways to reduce high bias in Machine Learning:
- Use a more complex model: One of the main reasons for high bias is the very simplified model. it will not be able to capture the complexity of the data. In such cases, we can make our mode more complex by increasing the number of hidden layers in the case of a deep neural network. Or we can use a more complex model like Polynomial regression for non-linear datasets, CNN for image processing, and RNN for sequence learning.
- Increase the number of features: By adding more features to train the dataset will increase the complexity of the model. And improve its ability to capture the underlying patterns in the data.
- Reduce Regularization of the model: Regularization techniques such as L1 or L2 regularization can help to prevent overfitting and improve the generalization ability of the model. if the model has a high bias, reducing the strength of regularization or removing it altogether can help to improve its performance.
- Increase the size of the training data: Increasing the size of the training data can help to reduce bias by providing the model with more examples to learn from the dataset.
What is Variance?
Variance is the measure of spread in data from its mean position. In machine learning variance is the amount by which the performance of a predictive model changes when it is trained on different subsets of the training data. More specifically, variance is the variability of the model that how much it is sensitive to another subset of the training dataset. i.e. how much it can adjust on the new subset of the training dataset.
Let Y be the actual values of the target variable, and 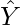 be the predicted values of the target variable. Then the variance of a model can be measured as the expected value of the square of the difference between predicted values and the expected value of the predicted values.
be the predicted values of the target variable. Then the variance of a model can be measured as the expected value of the square of the difference between predicted values and the expected value of the predicted values.
![Rendered by QuickLaTeX.com \text{Variance} = E[(\hat Y - E[\hat Y])^2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-90d24d7c9a008dd9586bf0b26f5b811c_l3.png)
where ![Rendered by QuickLaTeX.com E[\bar Y]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-13c6d7128798577b8d465ca85dcda920_l3.png) is the expected value of the predicted values. Here expected value is averaged over all the training data.
is the expected value of the predicted values. Here expected value is averaged over all the training data.
Variance errors are either low or high-variance errors.
- Low variance: Low variance means that the model is less sensitive to changes in the training data and can produce consistent estimates of the target function with different subsets of data from the same distribution. This is the case of underfitting when the model fails to generalize on both training and test data.
- High variance: High variance means that the model is very sensitive to changes in the training data and can result in significant changes in the estimate of the target function when trained on different subsets of data from the same distribution. This is the case of overfitting when the model performs well on the training data but poorly on new, unseen test data. It fits the training data too closely that it fails on the new training dataset.
Ways to Reduce the reduce Variance in Machine Learning:
- Cross-validation: By splitting the data into training and testing sets multiple times, cross-validation can help identify if a model is overfitting or underfitting and can be used to tune hyperparameters to reduce variance.
- Feature selection: By choosing the only relevant feature will decrease the model’s complexity. and it can reduce the variance error.
- Regularization: We can use L1 or L2 regularization to reduce variance in machine learning models
- Ensemble methods: It will combine multiple models to improve generalization performance. Bagging, boosting, and stacking are common ensemble methods that can help reduce variance and improve generalization performance.
- Simplifying the model: Reducing the complexity of the model, such as decreasing the number of parameters or layers in a neural network, can also help reduce variance and improve generalization performance.
- Early stopping: Early stopping is a technique used to prevent overfitting by stopping the training of the deep learning model when the performance on the validation set stops improving.
Mathematical Derivation for Total Error
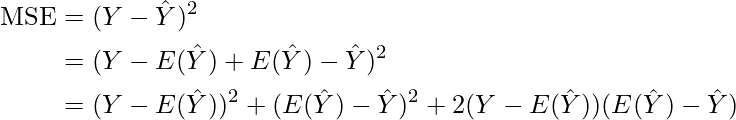
Applying the Expectations on both sides.
![Rendered by QuickLaTeX.com \begin{aligned} E[ (Y-\hat Y)^2] &= E[(Y-E(\hat Y))^2 + (E(\hat Y) -\hat Y)^2 + 2(Y-E(\hat Y))(E(\hat Y) -\hat Y)] \\ & = E[(Y-E(\hat Y))^2] + E[(E(\hat Y) -\hat Y)^2] + 2E[(Y-E(\hat Y))(E(\hat Y) -\hat Y)]] \\ & = [(Y-E(\hat Y))^2] + E[(E(\hat Y) -\hat Y)^2] + 2(Y-E(\hat Y))E[(E(\hat Y) -\hat Y)]] \\ & = [(Y-E(\hat Y))^2] + E[(E(\hat Y) -\hat Y)^2] + 2(Y-E(\hat Y))[E[E(\hat Y)] -E[\hat Y]] \\ & = [(Y-E(\hat Y))^2] + E[(E(\hat Y) -\hat Y)^2] + 2(Y-E(\hat Y))[E(\hat Y)] -E[\hat Y]] \\ & = [(Y-E(\hat Y))^2] + E[(E(\hat Y) -\hat Y)^2] + 2(Y-E(\hat Y))[0] \\ & = [(Y-E(\hat Y))^2] + E[(E(\hat Y) -\hat Y)^2] + 0 \\ &= [\text{Bias}^2] + \text{Variance} \end{aligned}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-219d84c0a6a9f68705efae2b7a3e1307_l3.png)
Different Combinations of Bias-Variance
There can be four combinations between bias and variance.
- High Bias, Low Variance: A model with high bias and low variance is said to be underfitting.
- High Variance, Low Bias: A model with high variance and low bias is said to be overfitting.
- High-Bias, High-Variance: A model has both high bias and high variance, which means that the model is not able to capture the underlying patterns in the data (high bias) and is also too sensitive to changes in the training data (high variance). As a result, the model will produce inconsistent and inaccurate predictions on average.
- Low Bias, Low Variance: A model that has low bias and low variance means that the model is able to capture the underlying patterns in the data (low bias) and is not too sensitive to changes in the training data (low variance). This is the ideal scenario for a machine learning model, as it is able to generalize well to new, unseen data and produce consistent and accurate predictions. But in practice, it’s not possible.

Bias-Variance Combinations
Now we know that the ideal case will be Low Bias and Low variance, but in practice, it is not possible. So, we trade off between Bias and variance to achieve a balanced bias and variance.
A model with balanced bias and variance is said to have optimal generalization performance. This means that the model is able to capture the underlying patterns in the data without overfitting or underfitting. The model is likely to be just complex enough to capture the complexity of the data, but not too complex to overfit the training data. This can happen when the model has been carefully tuned to achieve a good balance between bias and variance, by adjusting the hyperparameters and selecting an appropriate model architecture.
Bias Variance Tradeoff
If the algorithm is too simple (hypothesis with linear equation) then it may be on high bias and low variance condition and thus is error-prone. If algorithms fit too complex (hypothesis with high degree equation) then it may be on high variance and low bias. In the latter condition, the new entries will not perform well. Well, there is something between both of these conditions, known as a Trade-off or Bias Variance Trade-off. This tradeoff in complexity is why there is a tradeoff between bias and variance. An algorithm can’t be more complex and less complex at the same time. For the graph, the perfect tradeoff will be like this.
.png)
Bias-Variance Tradeoff
The technique by which we analyze the performance of the machine learning model is known as Bias Variance Decomposition. Now we give 1-1 example of Bias Variance Decomposition for classification and regression.
Bias Variance Decomposition for Classification and Regression
As per the formula, we have derived total error as the sum of Bias squares and variance. We try to make sure that the bias and the variance are comparable and one does not exceed the other by too much difference.
Python3
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import BaggingClassifier
from mlxtend.evaluate import bias_variance_decomp
import warnings
warnings.filterwarnings('ignore')
X, y = load_iris(return_X_y=True)
X_train, X_test,\
y_train, y_test = train_test_split(X, y,
test_size=0.25,
random_state=23,
shuffle=True,
stratify=y)
tree = DecisionTreeClassifier(random_state=123)
clf = BaggingClassifier(base_estimator=tree,
n_estimators=50,
random_state=23)
avg_expected_loss, avg_bias, \
avg_var = bias_variance_decomp(clf,
X_train, y_train,
X_test, y_test,
loss='0-1_loss',
random_seed=23)
print('Average expected loss: %.2f' % avg_expected_loss)
print('Average bias: %.2f' % avg_bias)
print('Average variance: %.2f' % avg_var)
|
Output:
Average expected loss: 0.06
Average bias: 0.05
Average variance: 0.02
Now let’s perform the same on the regression task. And check the values of the bias and variance.
Python3
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
import tensorflow as tf
from mlxtend.evaluate import bias_variance_decomp
import warnings
warnings.filterwarnings('ignore')
X, y = fetch_california_housing(return_X_y=True)
X_train, X_test,\
y_train, y_test = train_test_split(X, y,
test_size=0.25,
random_state=23,
shuffle=True)
model = tf.keras.Sequential([
tf.keras.layers.Dense(64, activation=tf.nn.relu),
tf.keras.layers.Dense(1)
])
optimizer = tf.keras.optimizers.Adam()
model.compile(loss='mean_squared_error',
optimizer=optimizer)
model.fit(X_train, y_train, epochs=25, verbose=0)
accuracy = model.evaluate(X_test, y_test)
print('Average: %.2f' % accuracy)
avg_expected_loss, avg_bias,\
avg_var = bias_variance_decomp(model,
X_train, y_train,
X_test, y_test,
loss='mse',
random_seed=23,
epochs=5,
verbose=0)
print('Average expected loss: %.2f' % avg_expected_loss)
print('Average bias: %.2f' % avg_bias)
print('Average variance: %.2f' % avg_var)
|
Output:
162/162 [==============================] - 0s 802us/step - loss: 0.9195
Average: 0.92
Average expected loss: 2.30
Average bias: 0.72
Average variance: 1.58
Share your thoughts in the comments
Please Login to comment...