Total number of possible Binary Search Trees and Binary Trees with n keys
Last Updated :
30 Dec, 2022
Total number of possible Binary Search Trees with n different keys (countBST(n)) = Catalan number Cn = (2n)! / ((n + 1)! * n!)
For n = 0, 1, 2, 3, … values of Catalan numbers are 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, …. So are numbers of Binary Search Trees.
Total number of possible Binary Trees with n different keys (countBT(n)) = countBST(n) * n!
Below is code for finding count of BSTs and Binary Trees with n numbers. The code to find n’th Catalan number is taken from here.
C++
#include <bits/stdc++.h>
using namespace std;
unsigned long int factorial(unsigned int n)
{
unsigned long int res = 1;
for (int i = 1; i <= n; ++i)
{
res *= i;
}
return res;
}
unsigned long int binomialCoeff(unsigned int n, unsigned int k)
{
unsigned long int res = 1;
if (k > n - k)
k = n - k;
for (int i = 0; i < k; ++i)
{
res *= (n - i);
res /= (i + 1);
}
return res;
}
unsigned long int catalan(unsigned int n)
{
unsigned long int c = binomialCoeff(2*n, n);
return c/(n+1);
}
unsigned long int countBST(unsigned int n)
{
unsigned long int count = catalan(n);
return count;
}
unsigned long int countBT(unsigned int n)
{
unsigned long int count = catalan(n);
return count * factorial(n);
}
int main()
{
int count1,count2, n = 5;
count1 = countBST(n);
count2 = countBT(n);
cout<<"Count of BST with "<<n<<" nodes is "<<count1<<endl;
cout<<"Count of binary trees with "<<n<<" nodes is "<<count2;
return 0;
}
|
Java
import java.io.*;
class GFG
{
static int factorial(int n)
{
int res = 1;
for (int i = 1; i <= n; ++i)
{
res *= i;
}
return res;
}
static int binomialCoeff(int n,
int k)
{
int res = 1;
if (k > n - k)
k = n - k;
for (int i = 0; i < k; ++i)
{
res *= (n - i);
res /= (i + 1);
}
return res;
}
static int catalan( int n)
{
int c = binomialCoeff(2 * n, n);
return c / (n + 1);
}
static int countBST( int n)
{
int count = catalan(n);
return count;
}
static int countBT(int n)
{
int count = catalan(n);
return count * factorial(n);
}
public static void main (String[] args)
{
int count1, count2, n = 5;
count1 = countBST(n);
count2 = countBT(n);
System.out.println("Count of BST with "+
n +" nodes is "+
count1);
System.out.println("Count of binary " +
"trees with "+
n + " nodes is " +
count2);
}
}
|
Python3
def factorial(n) :
res = 1
for i in range(1, n + 1):
res *= i
return res
def binomialCoeff(n, k):
res = 1
if (k > n - k):
k = n - k
for i in range(k):
res *= (n - i)
res //= (i + 1)
return res
def catalan(n):
c = binomialCoeff(2 * n, n)
return c // (n + 1)
def countBST(n):
count = catalan(n)
return count
def countBT(n):
count = catalan(n)
return count * factorial(n)
if __name__ == '__main__':
n = 5
count1 = countBST(n)
count2 = countBT(n)
print("Count of BST with", n, "nodes is", count1)
print("Count of binary trees with", n,
"nodes is", count2)
|
C#
using System;
class GFG
{
static int factorial(int n)
{
int res = 1;
for (int i = 1; i <= n; ++i)
{
res *= i;
}
return res;
}
static int binomialCoeff(int n,
int k)
{
int res = 1;
if (k > n - k)
k = n - k;
for (int i = 0; i < k; ++i)
{
res *= (n - i);
res /= (i + 1);
}
return res;
}
static int catalan(int n)
{
int c = binomialCoeff(2 * n, n);
return c / (n + 1);
}
static int countBST(int n)
{
int count = catalan(n);
return count;
}
static int countBT(int n)
{
int count = catalan(n);
return count * factorial(n);
}
static public void Main ()
{
int count1, count2, n = 5;
count1 = countBST(n);
count2 = countBT(n);
Console.WriteLine("Count of BST with "+
n +" nodes is "+
count1);
Console.WriteLine("Count of binary " +
"trees with "+
n + " nodes is " +
count2);
}
}
|
PHP
<?php
function factorial($n)
{
$res = 1;
for ($i = 1; $i <= $n; ++$i)
{
$res *= $i;
}
return $res;
}
function binomialCoeff($n, $k)
{
$res = 1;
if ($k > $n - $k)
$k = $n - $k;
for ($i = 0; $i < $k; ++$i)
{
$res *= ($n - $i);
$res = (int)$res / ($i + 1);
}
return $res;
}
function catalan($n)
{
$c = binomialCoeff(2 * $n, $n);
return (int)$c / ($n + 1);
}
function countBST($n)
{
$count = catalan($n);
return $count;
}
function countBT($n)
{
$count = catalan($n);
return $count *
factorial($n);
}
$count1;
$count2;
$n = 5;
$count1 = countBST($n);
$count2 = countBT($n);
echo "Count of BST with " , $n ,
" nodes is ", $count1,"\n";
echo "Count of binary trees with " ,
$n ," nodes is ",$count2;
?>
|
Javascript
<script>
function factorial(n)
{
let res = 1;
for (let i = 1; i <= n; ++i)
{
res *= i;
}
return res;
}
function binomialCoeff(n, k)
{
let res = 1;
if (k > n - k)
k = n - k;
for (let i = 0; i < k; ++i)
{
res *= (n - i);
res /= (i + 1);
}
return res;
}
function catalan(n)
{
let c = binomialCoeff(2 * n, n);
return c / (n + 1);
}
function countBST(n)
{
let count = catalan(n);
return count;
}
function countBT(n)
{
let count = catalan(n);
return count * factorial(n);
}
let count1, count2, n = 5;
count1 = countBST(n);
count2 = countBT(n);
document.write("Count of BST with "+
n +" nodes is "+
count1 + "</br>");
document.write("Count of binary " +
"trees with "+
n + " nodes is " +
count2);
</script>
|
Output:
Count of BST with 5 nodes is 42
Count of binary trees with 5 nodes is 5040
Time Complexity: O(n): The time complexity of the above code is O(n). It uses the Catalan number formula to calculate the number of possible binary search trees in O(n) time.
Auxiliary Space Complexity: O(1), The space complexity of the above code is O(1). No extra space is allocated.
Proof of Enumeration
Consider all possible binary search trees with each element at the root. If there are n nodes, then for each choice of root node, there are n – 1 non-root nodes and these non-root nodes must be partitioned into those that are less than a chosen root and those that are greater than the chosen root.
Let’s say node i is chosen to be the root. Then there are i – 1 nodes smaller than i and n – i nodes bigger than i. For each of these two sets of nodes, there is a certain number of possible subtrees.
Let t(n) be the total number of BSTs with n nodes. The total number of BSTs with i at the root is t(i – 1) t(n – i). The two terms are multiplied together because the arrangements in the left and right subtrees are independent. That is, for each arrangement in the left tree and for each arrangement in the right tree, you get one BST with i at the root.
Summing over i gives the total number of binary search trees with n nodes.
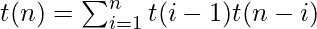
The base case is t(0) = 1 and t(1) = 1, i.e. there is one empty BST and there is one BST with one node.
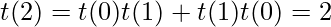
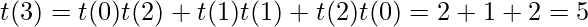
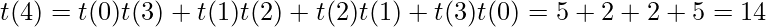
Also, the relationship countBT(n) = countBST(n) * n! holds. As for every possible BST, there can have n! binary trees where n is the number of nodes in BST.
Share your thoughts in the comments
Please Login to comment...