Preorder Traversal of Binary Tree

Preorder traversal is defined as a type of tree traversal that follows the Root-Left-Right policy where:

• The root node of the subtree is visited first.
• Then the left subtree  is traversed.
• At last, the right subtree is traversed.

Preorder traversal

Algorithm for Preorder Traversal of Binary Tree

The algorithm for preorder traversal is shown as follows:

Preorder(root):

1. Follow step 2 to 4 until root != NULL
2. Write root -> data
3. Preorder (root -> left)
4. Preorder (root -> right)
5. End loop

How does Preorder Traversal of Binary Tree work?

Consider the following tree:

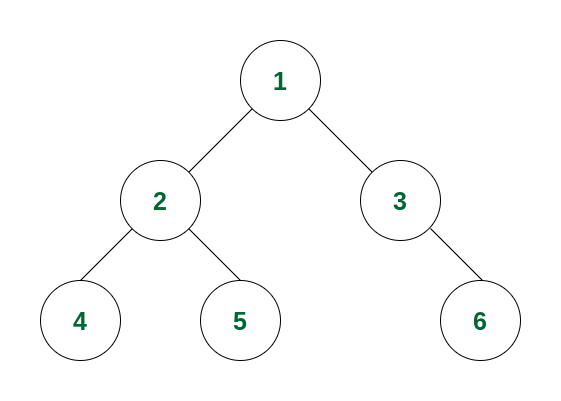
Example of Binary Tree

If we perform a preorder traversal in this binary tree, then the traversal will be as follows:

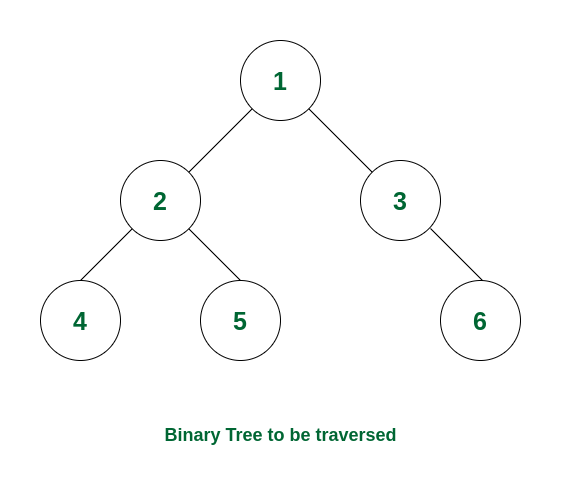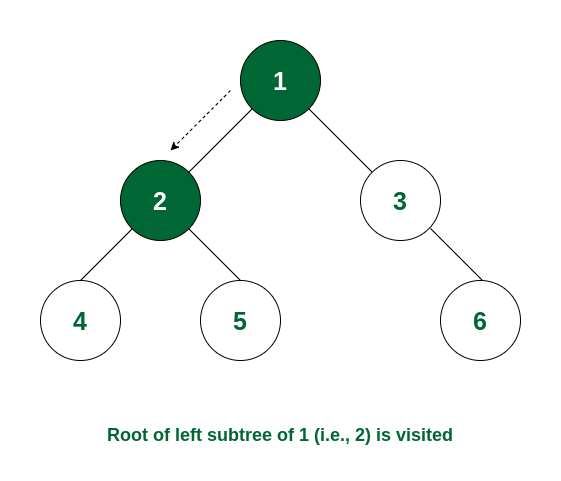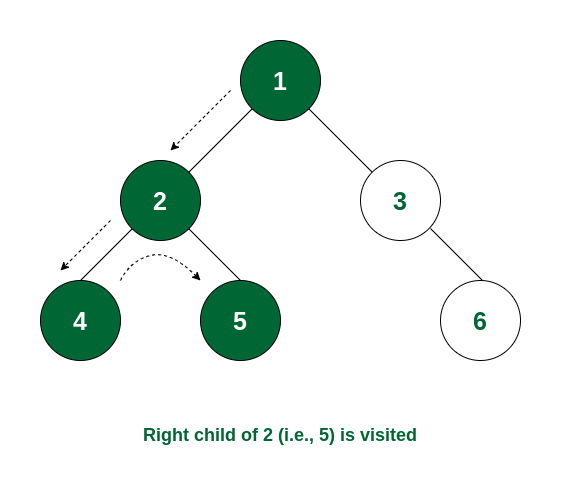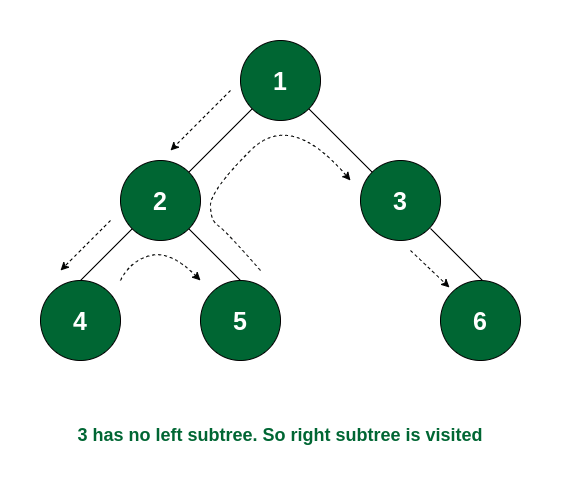
Step 1: At first the root will be visited, i.e. node 1.

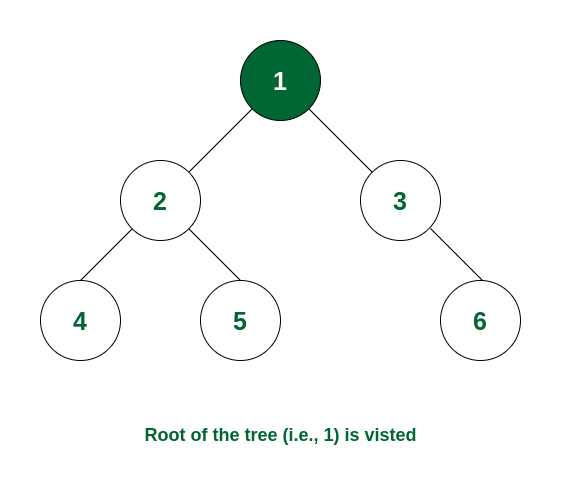
Node 1 is visited

Step 2: After this, traverse in the left subtree. Now the root of the left subtree is visited i.e., node 2 is visited.

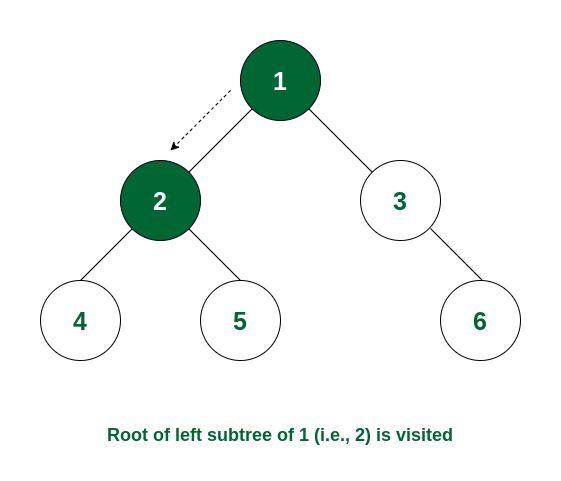
Node 2 is visited

Step 3: Again the left subtree of node 2 is traversed and the root of that subtree i.e., node 4 is visited.

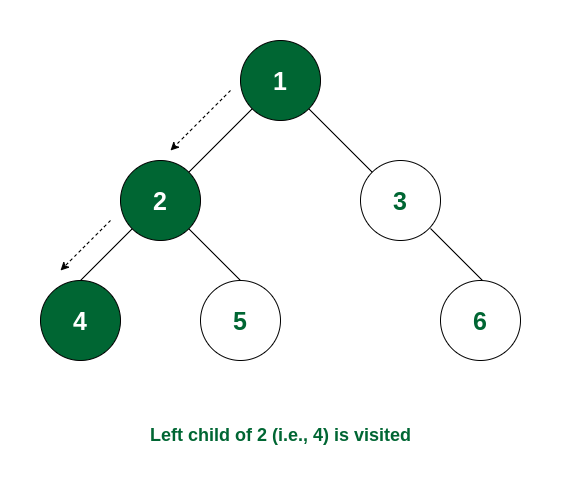
Node 4 is visited

Step 4: There is no subtree of 4 and the left subtree of node 2 is visited. So now the right subtree of node 2 will be traversed and the root of that subtree i.e., node 5 will be visited.

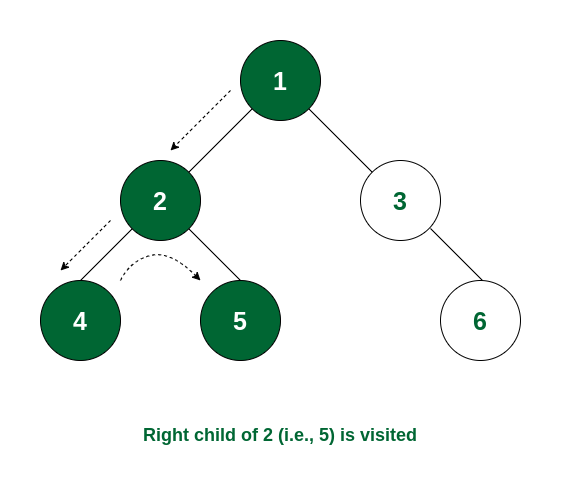
Node 5 is visited

Step 5: The left subtree of node 1 is visited. So now the right subtree of node 1 will be traversed and the root node i.e., node 3 is visited.

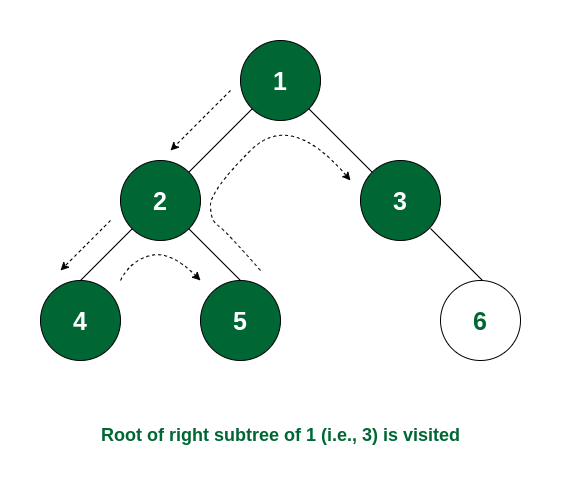
Node 3 is visited

Step 6: Node 3 has no left subtree. So the right subtree will be traversed and the root of the subtree i.e., node 6 will be visited. After that there is no node that is not yet traversed. So the traversal ends.

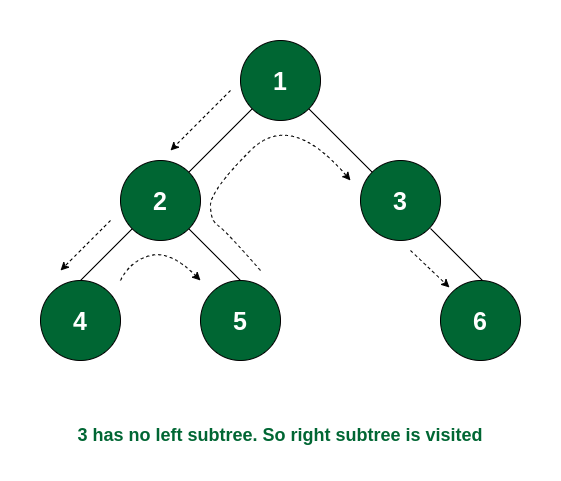
The complete tree is visited

So the order of traversal of nodes is 1 -> 2 -> 4 -> 5 -> 3 -> 6.

Program to Implement Preorder Traversal of Binary Tree

Below is the code implementation of the preorder traversal:

C++

// C++ program for preorder traversals

#include <bits/stdc++.h>
using namespace std;

// Structure of a Binary Tree Node
struct Node {
    int data;
    struct Node *left, *right;
    Node(int v)
    {
        data = v;
        left = right = NULL;
    }
};

// Function to print preorder traversal
void printPreorder(struct Node* node)
{
    if (node == NULL)
        return;

    // Deal with the node
    cout << node->data << " ";

    // Recur on left subtree
    printPreorder(node->left);

    // Recur on right subtree
    printPreorder(node->right);
}

// Driver code
int main()
{
    struct Node* root = new Node(1);
    root->left = new Node(2);
    root->right = new Node(3);
    root->left->left = new Node(4);
    root->left->right = new Node(5);
    root->right->right = new Node(6);

    // Function call
    cout << "Preorder traversal of binary tree is: \n";
    printPreorder(root);

    return 0;
}

Java

// Java program for preorder traversals

class Node {
    int data;
    Node left, right;

    public Node(int item) {
        data = item;
        left = right = null;
    }
}

class BinaryTree {
    Node root;

    BinaryTree() {
        root = null;
    }

    // Function to print preorder traversal
    void printPreorder(Node node) {
        if (node == null)
            return;

        // Deal with the node
        System.out.print(node.data + " ");

        // Recur on left subtree
        printPreorder(node.left);

        // Recur on right subtree
        printPreorder(node.right);
    }

    // Driver code
    public static void main(String[] args) {
        BinaryTree tree = new BinaryTree();

        // Constructing the binary tree
        tree.root = new Node(1);
        tree.root.left = new Node(2);
        tree.root.right = new Node(3);
        tree.root.left.left = new Node(4);
        tree.root.left.right = new Node(5);
        tree.root.right.right = new Node(6);

        // Function call
        System.out.println("Preorder traversal of binary tree is: ");
        tree.printPreorder(tree.root);
    }
}

Python3

# Python program for preorder traversals

# Structure of a Binary Tree Node
class Node:
    def __init__(self, v):
        self.data = v
        self.left = None
        self.right = None

# Function to print preorder traversal
def printPreorder(node):
    if node is None:
        return

    # Deal with the node
    print(node.data, end=' ')

    # Recur on left subtree
    printPreorder(node.left)

    # Recur on right subtree
    printPreorder(node.right)


# Driver code
if __name__ == '__main__':
    root = Node(1)
    root.left = Node(2)
    root.right = Node(3)
    root.left.left = Node(4)
    root.left.right = Node(5)
    root.right.right = Node(6)

    # Function call
    print("Preorder traversal of binary tree is:")
    printPreorder(root)

C#

// C# program for preorder traversals
using System;

// Structure of a Binary Tree Node
public class Node {
    public int data;
    public Node left, right;

    public Node(int v)
    {
        data = v;
        left = right = null;
    }
}

// Class to print preorder traversal
public class BinaryTree {
    // Function to print preorder traversal
    public static void printPreorder(Node node)
    {
        if (node == null)
            return;

        // Deal with the node
        Console.Write(node.data + " ");

        // Recur on left subtree
        printPreorder(node.left);

        // Recur on right subtree
        printPreorder(node.right);
    }

    // Driver code
    public static void Main()
    {
        Node root = new Node(1);
        root.left = new Node(2);
        root.right = new Node(3);
        root.left.left = new Node(4);
        root.left.right = new Node(5);
        root.right.right = new Node(6);

        // Function call
        Console.WriteLine(
            "Preorder traversal of binary tree is: ");
        printPreorder(root);
    }
}

// This code is contributed by Susobhan Akhuli

Javascript

// Structure of a Binary Tree Node
class Node {
  constructor(v) {
    this.data = v;
    this.left = null;
    this.right = null;
  }
}

// Function to print preorder traversal
function printPreorder(node) {
  if (node === null) {
    return;
  }

  // Deal with the node
  console.log(node.data);

  // Recur on left subtree
  printPreorder(node.left);

  // Recur on right subtree
  printPreorder(node.right);
}

// Driver code
function main() {
  const root = new Node(1);
  root.left = new Node(2);
  root.right = new Node(3);
  root.left.left = new Node(4);
  root.left.right = new Node(5);
  root.right.right = new Node(6);

  // Function call
  console.log("Preorder traversal of binary tree is:");
  printPreorder(root);
}

main();

Output

Preorder traversal of binary tree is: 
1 2 4 5 3 6 

Explanation:

How preorder traversal works

Complexity Analysis:

Time Complexity: O(N) where N is the total number of nodes. Because it traverses all the nodes at least once.
Auxiliary Space:

• O(1) if no recursion stack space is considered. 
• Otherwise, O(h) where h is the height of the tree
• In the worst case, h can be the same as N (when the tree is a skewed tree)
• In the best case, h can be the same as logN (when the tree is a complete tree)

Use cases of Preorder Traversal:

Some use cases of preorder traversal are:

• This is often used for creating a copy of a tree.
• It is also useful to get the prefix expression from an expression tree.