Total number of Spanning Trees in a Graph
Last Updated :
26 Mar, 2024
If a graph is a complete graph with n vertices, then total number of spanning trees is n(n-2) where n is the number of nodes in the graph. In complete graph, the task is equal to counting different labeled trees with n nodes for which have Cayley’s formula.
What if graph is not complete?
Follow the given procedure:
- STEP 1: Create Adjacency Matrix for the given graph.
- STEP 2: Replace all the diagonal elements with the degree of nodes. For eg. element at (1,1) position of adjacency matrix will be replaced by the degree of node 1, element at (2,2) position of adjacency matrix will be replaced by the degree of node 2, and so on.
- STEP 3: Replace all non-diagonal 1’s with -1.
- STEP 4: Calculate co-factor for any element.
- STEP 5: The cofactor that you get is the total number of spanning tree for that graph.
Consider the following graph:
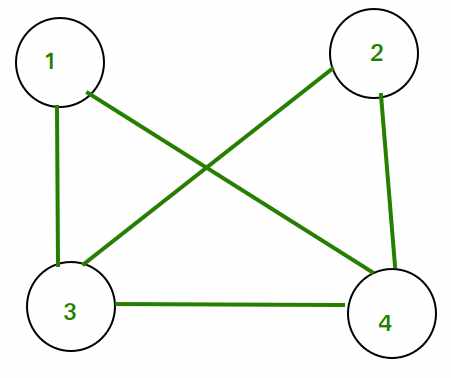
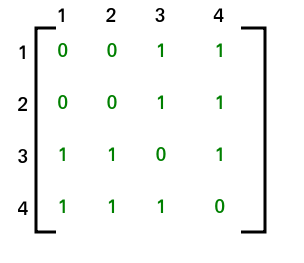
Adjacency Matrix for the above graph will be as follows:
After applying STEP 2 and STEP 3, adjacency matrix will look like
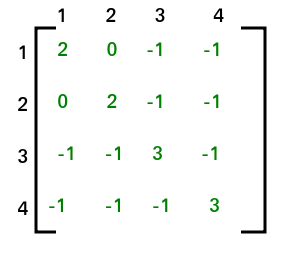
The co-factor for (1, 1) is 8. Hence total no. of spanning tree that can be formed is 8.
NOTE: Co-factor for all the elements will be same. Hence we can compute co-factor for any element of the matrix. This method is also known as Kirchhoff’s Theorem. It can be applied to complete graphs also.
let’s see another example to solve these problems by making use of the Laplacian matrix.
A Laplacian matrix L,
where L[i, i] is the degree of node i and L[i, j] = -1 if there is an edge between nodes i and j, and otherwise L[i, j] = 0.
Kirchhoff’s theorem provides a way to calculate the number of spanning trees for a given graph as a determinant of a special matrix.
consider the following graph,

the undirected graph
All possible spanning trees are as follows

three spanning trees
In order to calculate the number of spanning trees, construct a Laplacian matrix L, where L[i, i] is the degree of node i and L[i, j] = ?1 if there is an edge between nodes i and j, and otherwise L[i, j] = 0.
for the above graph, The Laplacian matrix will look like this
The number of spanning trees equals the determinant of a matrix.
The Determinant of a matrix that can be obtained when we remove any row and any column from L.
For example, if we remove the first row and column, the result will be,
The determinant is always the same, regardless of which row and column we remove from L.
C++
#include<bits/stdc++.h>
using namespace std;
#define MAX 100
#define MOD 1000000007
void multiply(int A[MAX][MAX], int B[MAX][MAX], int C[MAX][MAX])
{
for (int i = 0; i < MAX; i++)
for (int j = 0; j < MAX; j++)
for (int k = 0; k < MAX; k++)
C[i][j] = (C[i][j] + (A[i][k] * B[k][j])%MOD)%MOD;
}
void power(int A[MAX][MAX], int N, int result[MAX][MAX])
{
int temp[MAX][MAX];
for (int i = 0; i < MAX; i++)
for (int j = 0; j < MAX; j++)
result[i][j] = (i == j);
while (N>0)
{
if (N%2 == 1)
{
multiply(A, result, temp);
for (int i=0; i<MAX; i++)
for (int j=0; j<MAX; j++)
result[i][j] = temp[i][j];
}
N = N/2;
multiply(A, A, temp);
for (int i=0; i<MAX; i++)
for (int j=0; j<MAX; j++)
A[i][j] = temp[i][j];
}
}
int numOfSpanningTree(int graph[][MAX], int V)
{
int result[MAX][MAX] = {0};
int temp[MAX][MAX] = {0};
for (int i = 0; i < V; i++)
for (int j = 0; j < V; j++)
temp[i][j] = graph[i][j];
power(temp, V-2, result);
int ans = 0;
for (int i = 0; i < V; i++)
for (int j = 0; j < V; j++)
ans = (ans + result[i][j])%MOD;
return ans;
}
int main()
{
int V = 4;
int E = 5;
int graph[][MAX] = {
{0, 1, 1, 1},
{1, 0, 1, 1},
{1, 1, 0, 1},
{1, 1, 1, 0}
};
cout << numOfSpanningTree(graph, V);
return 0;
}
|
Java
import java.util.*;
public class Main {
static final int MAX = 100;
static final int MOD = 1000000007;
static void multiply(int A[][], int B[][], int C[][])
{
for (int i = 0; i < MAX; i++)
for (int j = 0; j < MAX; j++)
for (int k = 0; k < MAX; k++)
C[i][j] = (int)((C[i][j]
+ (A[i][k] * B[k][j])
% MOD)
% MOD);
}
static void power(int A[][], int N, int result[][])
{
int temp[][] = new int[MAX][MAX];
for (int i = 0; i < MAX; i++)
for (int j = 0; j < MAX; j++)
result[i][j] = (i == j) ? 1 : 0;
while (N > 0) {
if (N % 2 == 1) {
multiply(A, result, temp);
for (int i = 0; i < MAX; i++)
for (int j = 0; j < MAX; j++)
result[i][j] = temp[i][j];
}
N = N / 2;
multiply(A, A, temp);
for (int i = 0; i < MAX; i++)
for (int j = 0; j < MAX; j++)
A[i][j] = temp[i][j];
}
}
static int numOfSpanningTree(int graph[][], int V)
{
int result[][] = new int[MAX][MAX];
int temp[][] = new int[MAX][MAX];
for (int i = 0; i < V; i++)
for (int j = 0; j < V; j++)
temp[i][j] = graph[i][j];
power(temp, V - 2, result);
int ans = 0;
for (int i = 0; i < V; i++)
for (int j = 0; j < V; j++)
ans = (int)((ans + result[i][j]) % MOD);
return ans;
}
public static void main(String[] args)
{
int V = 4;
int E = 5;
int graph[][] = { { 0, 1, 1, 1 },
{ 1, 0, 1, 1 },
{ 1, 1, 0, 1 },
{ 1, 1, 1, 0 } };
System.out.println(numOfSpanningTree(graph, V));
}
}
|
C#
using System;
class GFG
{
static int MAX = 100;
static int MOD = 1000000007;
static void multiply(int[,] A, int[,] B, int[,] C)
{
for (int i = 0; i < MAX; i++)
for (int j = 0; j < MAX; j++)
for (int k = 0; k < MAX; k++)
C[i, j] = (C[i, j] + (A[i, k] * B[k, j]) % MOD) % MOD;
}
static void power(int[,] A, int N, int[,] result)
{
int[,] temp = new int[MAX, MAX];
for (int i = 0; i < MAX; i++)
for (int j = 0; j < MAX; j++)
result[i, j] = (i == j) ? 1 : 0;
while (N > 0)
{
if (N % 2 == 1)
{
multiply(A, result, temp);
for (int i = 0; i < MAX; i++)
for (int j = 0; j < MAX; j++)
result[i, j] = temp[i, j];
}
N = N / 2;
multiply(A, A, temp);
for (int i = 0; i < MAX; i++)
for (int j = 0; j < MAX; j++)
A[i, j] = temp[i, j];
}
}
static int numOfSpanningTree(int[,] graph, int V)
{
int[,] result = new int[MAX, MAX];
int[,] temp = new int[MAX, MAX];
for (int i = 0; i < V; i++)
for (int j = 0; j < V; j++)
temp[i, j] = graph[i, j];
power(temp, V - 2, result);
int ans = 0;
for (int i = 0; i < V; i++)
for (int j = 0; j < V; j++)
ans = (ans + result[i, j]) % MOD;
return ans;
}
public static void Main()
{
int V = 4;
int E = 5;
int[,] graph = {
{0, 1, 1, 1},
{1, 0, 1, 1},
{1, 1, 0, 1},
{1, 1, 1, 0}
};
Console.Write(numOfSpanningTree(graph, V));
}
}
|
Python3
MAX = 100
MOD = 1000000007
def multiply(A, B, C):
for i in range(MAX):
for j in range(MAX):
C[i][j] = 0
for k in range(MAX):
C[i][j] = (C[i][j] + (A[i][k] * B[k][j]) % MOD) % MOD
def power(A, N, result):
temp = [[0] * MAX for i in range(MAX)]
for i in range(MAX):
for j in range(MAX):
result[i][j] = 1 if i == j else 0
while N > 0:
if N % 2 == 1:
multiply(A, result, temp)
for i in range(MAX):
for j in range(MAX):
result[i][j] = temp[i][j]
N = N // 2
multiply(A, A, temp)
for i in range(MAX):
for j in range(MAX):
A[i][j] = temp[i][j]
def numOfSpanningTree(graph, V):
result = [[0] * MAX for i in range(MAX)]
temp = [[0] * MAX for i in range(MAX)]
for i in range(V):
for j in range(V):
temp[i][j] = graph[i][j]
power(temp, V - 2, result)
ans = 0
for i in range(V):
for j in range(V):
ans = (ans + result[i][j]) % MOD
return ans
if __name__ == '__main__':
V = 4
E = 5
graph = [[0, 1, 1, 1],
[1, 0, 1, 1],
[1, 1, 0, 1],
[1, 1, 1, 0]]
print(numOfSpanningTree(graph, V))
|
Javascript
const MAX = 100;
const MOD = 1000000007;
function multiply(A, B, C) {
for (let i = 0; i < MAX; i++) {
for (let j = 0; j < MAX; j++) {
C[i][j] = 0;
for (let k = 0; k < MAX; k++) {
C[i][j] = (C[i][j] + (A[i][k] * B[k][j]) % MOD) % MOD;
}
}
}
}
function power(A, N, result) {
let temp = new Array(MAX).fill().map(() => new Array(MAX).fill(0));
for (let i = 0; i < MAX; i++) {
result[i][i] = 1;
}
while (N > 0) {
if (N % 2 == 1) {
multiply(A, result, temp);
for (let i = 0; i < MAX; i++) {
for (let j = 0; j < MAX; j++) {
result[i][j] = temp[i][j];
}
}
}
N = Math.floor(N / 2);
multiply(A, A, temp);
for (let i = 0; i < MAX; i++) {
for (let j = 0; j < MAX; j++) {
A[i][j] = temp[i][j];
}
}
}
}
function numOfSpanningTree(graph, V) {
let result = new Array(MAX).fill().map(() => new Array(MAX).fill(0));
let temp = new Array(MAX).fill().map(() => new Array(MAX).fill(0));
for (let i = 0; i < V; i++) {
for (let j = 0; j < V; j++) {
temp[i][j] = graph[i][j];
}
}
power(temp, V - 2, result);
let ans = 0;
for (let i = 0; i < V; i++) {
for (let j = 0; j < V; j++) {
ans = (ans + result[i][j]) % MOD;
}
} ans = ans+ans;
return ans;
}
const V = 4;
const E = 5;
const graph = [[0, 1, 1, 1], [1, 0, 1, 1], [1, 1, 0, 1], [1, 1, 1, 0]];
console.log(numOfSpanningTree(graph, V));
|
Time Complexity: The given program uses the Matrix Chain Multiplication algorithm to find the number of spanning trees in a given graph. The algorithm works by computing the (V-2)th power of the adjacency matrix of the graph, where V is the number of vertices in the graph. The number of spanning trees in the graph is equal to the sum of all the entries in the resulting matrix.
The time complexity of the program is determined by the matrix multiplication and exponentiation operations. The matrix multiplication operation takes O(V^3) time, and it is performed N times, where N is the power to which the adjacency matrix is raised. Since N can be as large as V-2, the total time complexity of the program is O(V^3 * log N).
Space Complexity:
The space complexity of the program is determined by the size of the adjacency matrix and the result matrix. Since the matrices are of size VxV, the space complexity of the program is O(V^2). In addition, there are some temporary matrices created during the matrix multiplication and exponentiation operations, but they are of the same size as the input matrices and do not contribute significantly to the space complexity.
Overall, the program is efficient for finding the number of spanning trees in small to medium-sized graphs. However, for large graphs, the time and space complexity of the program may become a bottleneck, and alternative algorithms may be more appropriate.
NOTE:
Cayley’s formula is a special case of Kirchhoff’s theorem because, in a complete graph of n nodes, the determinant is equal to nn-2
Share your thoughts in the comments
Please Login to comment...