Maximum Possible Edge Disjoint Spanning Tree From a Complete Graph

Give a complete graph with N-vertices. The task is to find out the maximum number of edge-disjoint spanning tree possible.
Edge-disjoint Spanning Tree is a spanning tree where no two trees in the set have an edge in common.

Examples:

Input : N = 4
Output : 2

Input : N = 5
Output : 2 

The maximum number of possible Edge-Disjoint Spanning tree from a complete graph with N vertices can be given as, 

Max Edge-disjoint spanning tree = floor(N / 2)

Let’s look at some examples:

Example 1:

Complete graph with 4 vertices

All possible Edge-disjoint spanning trees for the above graph are: 

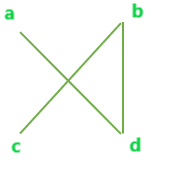
A

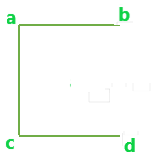
B

Example 2: 

Complete graph with 5 vertices

All possible Edge-disjoint spanning trees for the above graph are: 

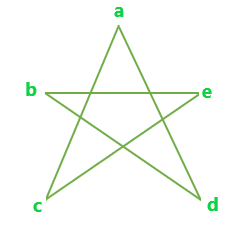
A

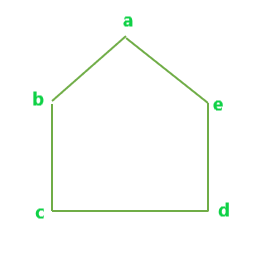
B

Implementation: Below is the program to find the maximum number of edge-disjoint spanning trees possible. 

C++

// C++ program to find the maximum number of
// Edge-Disjoint Spanning tree possible

#include <bits/stdc++.h>
using namespace std;

// Function to calculate max number of
// Edge-Disjoint Spanning tree possible
float edgeDisjoint(int n)
{
    float result = 0;

    result = floor(n / 2);

    return result;
}

// Driver code
int main()
{
    int n = 4;

    cout << edgeDisjoint(n);

    return 0;
}

Java

// Java program to find the maximum
// number of Edge-Disjoint Spanning
// tree possible
import java.io.*;

class GFG
{

// Function to calculate max number
// of Edge-Disjoint Spanning tree
// possible
static double edgeDisjoint(int n)
{
    double result = 0;

    result = Math.floor(n / 2);

    return result;
}

// Driver Code
public static void main(String[] args)
{
    int n = 4;
    System.out.println((int)edgeDisjoint(n));
}
}

// This code is contributed
// by Naman_Garg

Python3

# Python 3 to find the maximum
# number of Edge-Disjoint
# Spanning tree possible
import math

# Function to calculate max
# number of Edge-Disjoint
# Spanning tree possible
def edgeDisjoint(n):

    result = 0

    result = math.floor(n / 2)

    return result

# Driver Code
if __name__ == "__main__" :

    n = 4

    print(int(edgeDisjoint(n)))

# This Code is contributed
# by Naman_Garg

C#

// C# program to find the maximum number of
// Edge-Disjoint Spanning tree possible
using System;

class GFG
{

// Function to calculate max number of
// Edge-Disjoint Spanning tree possible
static double edgeDisjoint(double n)
{
    double result = 0;

    result = Math.Floor(n / 2);

    return result;
}

// Driver Code
public static void Main()
{
    int n = 4;

    Console.Write(edgeDisjoint(n));
}
}

// This code is contributed
// by Sanjit_Prasad

PHP

<?php
// PHP program to find the maximum
// number of Edge-Disjoint Spanning
// tree possible

// Function to calculate max number of
// Edge-Disjoint Spanning tree possible
function edgeDisjoint($n)
{
    $result = 0;

    $result = floor($n / 2);

    return $result;
}

// Driver code
$n = 4;

echo edgeDisjoint($n);

// This code is contributed
// by Ankita Saini
?>

Javascript

<script>

// Javascript program to find the maximum number of
// Edge-Disjoint Spanning tree possible

// Function to calculate max number of
// Edge-Disjoint Spanning tree possible
function edgeDisjoint(n)
{
    var result = 0;

    result = Math.floor(n / 2);

    return result;
}

// Driver code
var n = 4;
document.write( edgeDisjoint(n));

</script>

Output

2

Time Complexity: O(1)
Auxiliary Space: O(1)