Topological Sort of a graph using departure time of vertex
Last Updated :
20 Feb, 2023
Given a Directed Acyclic Graph (DAG), find Topological Sort of the graph.
Topological sorting for Directed Acyclic Graph (DAG) is a linear ordering of vertices such that for every directed edge uv, vertex u comes before v in the ordering. Topological Sorting for a graph is not possible if the graph is not a DAG.
For example, a topological sorting of the following graph is “5 4 2 3 1 0”. There can be more than one topological sorting for a graph. For example, another topological sorting of the following graph is “4 5 2 3 1 0”.
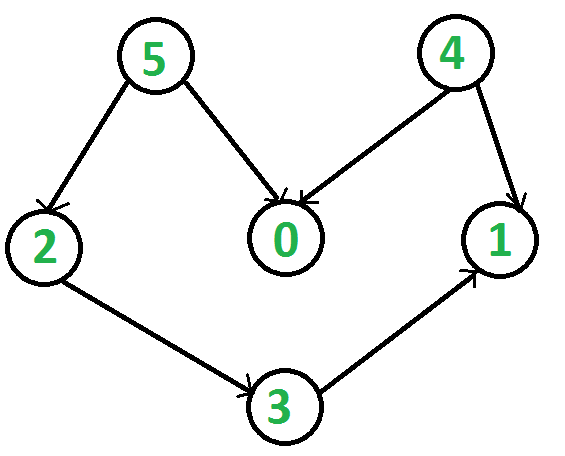
Please note that the first vertex in topological sorting is always a vertex with in-degree as 0 (a vertex with no incoming edges). For above graph, vertex 4 and 5 have no incoming edges.
We have already discussed a DFS-based algorithm using stack and Kahn’s Algorithm for Topological Sorting. We have also discussed how to print all topological sorts of the DAG here. In this post, another DFS based approach is discussed for finding Topological sort of a graph by introducing concept of arrival and departure time of a vertex in DFS.
What is Arrival Time & Departure Time of Vertices in DFS?
In DFS, Arrival Time is the time at which the vertex was explored for the first time and Departure Time is the time at which we have explored all the neighbors of the vertex and we are ready to backtrack.
How to find Topological Sort of a graph using departure time?
To find Topological Sort of a graph, we run DFS starting from all unvisited vertices one by one. For any vertex, before exploring any of its neighbors, we note the arrival time of that vertex and after exploring all the neighbors of the vertex, we note its departure time. Please note only departure time is needed to find Topological Sort of a graph, so we can skip arrival time of vertex. Finally, after we have visited all the vertices of the graph, we print the vertices in order of their decreasing departure time which is our desired Topological Order of Vertices.
Below is C++ implementation of above idea –
C++
#include <bits/stdc++.h>
using namespace std;
class Graph {
int V;
list<int>* adj;
public:
Graph(int);
~Graph();
void addEdge(int, int);
void DFS(int, vector<bool>&, vector<int>&, int&);
void topologicalSort();
};
Graph::Graph(int V)
{
this->V = V;
this->adj = new list<int>[V];
}
Graph::~Graph() { delete[] this->adj; }
void Graph::addEdge(int v, int w)
{
adj[v].push_back(w);
}
void Graph::DFS(int v, vector<bool>& visited,
vector<int>& departure, int& time)
{
visited[v] = true;
for (int i : adj[v])
if (!visited[i])
DFS(i, visited, departure, time);
departure[time++] = v;
}
void Graph::topologicalSort()
{
vector<int> departure(V, -1);
vector<bool> visited(V, false);
int time = 0;
for (int i = 0; i < V; i++) {
if (visited[i] == 0) {
DFS(i, visited, departure, time);
}
}
for (int i = V - 1; i >= 0; i--)
cout << departure[i] << " ";
}
int main()
{
Graph g(6);
g.addEdge(5, 2);
g.addEdge(5, 0);
g.addEdge(4, 0);
g.addEdge(4, 1);
g.addEdge(2, 3);
g.addEdge(3, 1);
cout << "Topological Sort of the given graph is \n";
g.topologicalSort();
return 0;
}
|
Python3
def addEdge(u, v):
global adj
adj[u].append(v)
def DFS(v):
global visited, departure, time
visited[v] = 1
for i in adj[v]:
if visited[i] == 0:
DFS(i)
departure[time] = v
time += 1
def topologicalSort():
for i in range(V):
if(visited[i] == 0):
DFS(i)
for i in range(V - 1, -1, -1):
print(departure[i], end = " ")
if __name__ == '__main__':
V,time, adj, visited, departure = 6, 0, [[] for i in range(7)], [0 for i in range(7)],[-1 for i in range(7)]
addEdge(5, 2)
addEdge(5, 0)
addEdge(4, 0)
addEdge(4, 1)
addEdge(2, 3)
addEdge(3, 1)
print("Topological Sort of the given graph is")
topologicalSort()
|
C#
using System;
using System.Collections.Generic;
public class Graph {
private int V;
private List<int>[] adj;
public Graph(int v)
{
V = v;
adj = new List<int>[ v ];
for (int i = 0; i < v; i++)
adj[i] = new List<int>();
}
public void AddEdge(int v, int w)
{
adj[v].Add(w);
}
private void DFS(int v, bool[] visited, int[] departure,
ref int time)
{
visited[v] = true;
foreach(int i in adj[v])
{
if (!visited[i])
DFS(i, visited, departure, ref time);
}
departure[time++] = v;
}
public void TopologicalSort()
{
int[] departure = new int[V];
for (int i = 0; i < V; i++)
departure[i] = -1;
bool[] visited = new bool[V];
int time = 0;
for (int i = 0; i < V; i++) {
if (visited[i] == false) {
DFS(i, visited, departure, ref time);
}
}
for (int i = V - 1; i >= 0; i--)
Console.Write(departure[i] + " ");
Console.WriteLine();
}
}
class GFG {
static void Main(string[] args)
{
Graph g = new Graph(6);
g.AddEdge(5, 2);
g.AddEdge(5, 0);
g.AddEdge(4, 0);
g.AddEdge(4, 1);
g.AddEdge(2, 3);
g.AddEdge(3, 1);
Console.WriteLine(
"Topological Sort of the given graph is");
g.TopologicalSort();
}
}
|
Javascript
<script>
let adj=new Array(7);
for(let i=0;i<adj.length;i++)
{
adj[i]=[];
}
let V=6;
let time=0;
let visited=new Array(7);
let departure =new Array(7);
for(let i=0;i<7;i++)
{
visited[i]=0;
departure[i]=-1;
}
function addEdge(u, v)
{
adj[u].push(v)
}
function DFS(v)
{
visited[v] = 1;
for(let i=0;i<adj[v].length;i++)
{
if(visited[adj[v][i]]==0)
DFS(adj[v][i]);
}
departure[time] = v
time += 1
}
function topologicalSort()
{
for(let i=0;i<V;i++)
{
if(visited[i] == 0)
DFS(i)
}
for(let i=V-1;i>=0;i--)
{
document.write(departure[i]+" ");
}
}
addEdge(5, 2);
addEdge(5, 0);
addEdge(4, 0);
addEdge(4, 1);
addEdge(2, 3);
addEdge(3, 1);
document.write(
"Topological Sort of the given graph is<br>"
);
topologicalSort()
</script>
|
Java
import java.util.ArrayList;
public class GFG {
int V;
ArrayList<ArrayList<Integer> > adj;
int time = 0;
public GFG(int v)
{
V = v;
adj = new ArrayList<>();
for (int i = 0; i < v; i++)
adj.add(new ArrayList<>());
}
public void AddEdge(int v, int w)
{
adj.get(v).add(w);
}
private void DFS(int v, boolean[] visited,
int[] departure)
{
visited[v] = true;
for (int i : adj.get(v)) {
if (!visited[i])
DFS(i, visited, departure);
}
departure[time++] = v;
}
public void TopologicalSort()
{
int[] departure = new int[V];
for (int i = 0; i < V; i++)
departure[i] = -1;
boolean[] visited = new boolean[V];
for (int i = 0; i < V; i++) {
if (!visited[i]) {
DFS(i, visited, departure);
}
}
for (int i = V - 1; i >= 0; i--)
System.out.print(departure[i] + " ");
}
public static void main(String[] args)
{
GFG g = new GFG(6);
g.AddEdge(5, 2);
g.AddEdge(5, 0);
g.AddEdge(4, 0);
g.AddEdge(4, 1);
g.AddEdge(2, 3);
g.AddEdge(3, 1);
System.out.println(
"Topological Sort of the given graph is");
g.TopologicalSort();
}
}
|
Output
Topological Sort of the given graph is
5 4 2 3 1 0
Time Complexity of above solution is O(V + E).
Space Complexity of this algorithm is O(V). This is because we use a vector to store the departure time of each vertex, which is of size V.
Share your thoughts in the comments
Please Login to comment...