Check if a given directed graph is strongly connected | Set 2 (Kosaraju using BFS)

Given a directed graph, find out whether the graph is strongly connected or not. A directed graph is strongly connected if there is a path between any two pairs of vertices. There are different methods to check the connectivity of directed graph but one of the optimized method is Kosaraju’s DFS based simple algorithm. 

Kosaraju’s BFS based simple algorithm also work on the same principle as DFS based algorithm does. 

Following is Kosaraju’s BFS based simple algorithm
that does two BFS traversals of graph:
1) Initialize all vertices as not visited.

2) Do a BFS traversal of graph starting from 
   any arbitrary vertex v. If BFS traversal 
   doesn’t visit all vertices, then return false.

3) Reverse all edges (or find transpose or reverse 
   of graph)

4) Mark all vertices as not visited in reversed graph.

5) Again do a BFS traversal of reversed graph starting
   from same vertex v (Same as step 2). If BFS traversal
   doesn’t visit all vertices, then return false. 
   Otherwise, return true.

The idea is again simple if every node can be reached from a vertex v, and every node can reach same vertex v, then the graph is strongly connected. In step 2, we check if all vertices are reachable from v. In step 5, we check if all vertices can reach v (In reversed graph, if all vertices are reachable from v, then all vertices can reach v in original graph).

Explanation with some examples: 

Example 1 : 
Given a directed to check if it is strongly connected or not. 

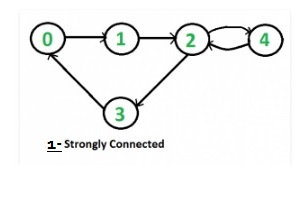
• step 1: Starting with vertex 2 BFS obtained is 2 3 4 0 1
• step 2: After reversing the given graph we got listed graph. 

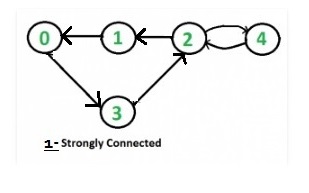
• step 3: Again after starting with vertex 2 the BFS is 2 1 4 0 3
• step 4: No vertex in both case (step 1 & step 3) remains unvisited.
• step 5: So, given graph is strongly connected.

Example 2 : 

Given a directed to check if it is strongly connected or not. 

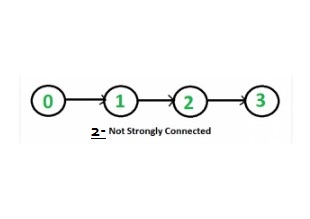
• step 1: Starting with vertex 2 BFS obtained is 2 3 4 
• step 2: After reversing the given graph we got listed graph. 

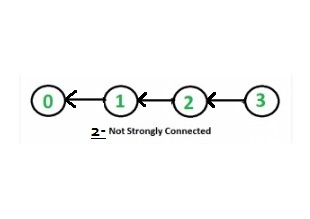
• step 3: Again after starting with vertex 2 the BFS is 2 1 0 
• step 4: vertex 0, 1 in original graph and 3, 4 in reverse graph remains unvisited.
• step 5: So, given graph is not strongly connected.

Following is the implementation of above algorithm. 

C++

// C++ program to check if a given directed graph
// is strongly connected or not with BFS use
#include <bits/stdc++.h>
using namespace std;

class Graph
{
    int V;    // No. of vertices
    list<int> *adj;    // An array of adjacency lists

    // A recursive function to print DFS starting from v
    void BFSUtil(int v, bool visited[]);
public:

    // Constructor and Destructor
    Graph(int V) { this->V = V;  adj = new list<int>[V];}
    ~Graph() { delete [] adj; }

    // Method to add an edge
    void addEdge(int v, int w);

    // The main function that returns true if the
    // graph is strongly connected, otherwise false
    bool isSC();

    // Function that returns reverse (or transpose)
    // of this graph
    Graph getTranspose();
};

// A recursive function to print DFS starting from v
void Graph::BFSUtil(int v, bool visited[])
{
    // Create a queue for BFS
    list<int> queue;

    // Mark the current node as visited and enqueue it
    visited[v] = true;
    queue.push_back(v);

    // 'i' will be used to get all adjacent vertices
    // of a vertex
    list<int>::iterator i;

    while (!queue.empty())
    {
        // Dequeue a vertex from queue
        v = queue.front();
        queue.pop_front();

        // Get all adjacent vertices of the dequeued vertex s
        // If a adjacent has not been visited, then mark it
        // visited and enqueue it
        for (i = adj[v].begin(); i != adj[v].end(); ++i)
        {
            if (!visited[*i])
            {
                visited[*i] = true;
                queue.push_back(*i);
            }
        }
    }
}

// Function that returns reverse (or transpose) of this graph
Graph Graph::getTranspose()
{
    Graph g(V);
    for (int v = 0; v < V; v++)
    {
        // Recur for all the vertices adjacent to this vertex
        list<int>::iterator i;
        for (i = adj[v].begin(); i != adj[v].end(); ++i)
            g.adj[*i].push_back(v);
    }
    return g;
}

void Graph::addEdge(int v, int w)
{
    adj[v].push_back(w); // Add w to v’s list.
}

// The main function that returns true if graph
// is strongly connected
bool Graph::isSC()
{
    // Step 1: Mark all the vertices as not
    // visited (For first BFS)
    bool visited[V];
    for (int i = 0; i < V; i++)
        visited[i] = false;

    // Step 2: Do BFS traversal starting
    // from first vertex.
    BFSUtil(0, visited);

    // If BFS traversal doesn’t visit all
    // vertices, then return false.
    for (int i = 0; i < V; i++)
        if (visited[i] == false)
             return false;

    // Step 3: Create a reversed graph
    Graph gr = getTranspose();

    // Step 4: Mark all the vertices as not
    // visited (For second BFS)
    for(int i = 0; i < V; i++)
        visited[i] = false;

    // Step 5: Do BFS for reversed graph
    // starting from first vertex.
    // Starting Vertex must be same starting
    // point of first DFS
    gr.BFSUtil(0, visited);

    // If all vertices are not visited in
    // second DFS, then return false
    for (int i = 0; i < V; i++)
        if (visited[i] == false)
             return false;

    return true;
}

// Driver program to test above functions
int main()
{
    // Create graphs given in the above diagrams
    Graph g1(5);
    g1.addEdge(0, 1);
    g1.addEdge(1, 2);
    g1.addEdge(2, 3);
    g1.addEdge(3, 0);
    g1.addEdge(2, 4);
    g1.addEdge(4, 2);
    g1.isSC()? cout << "Yes\n" : cout << "No\n";

    Graph g2(4);
    g2.addEdge(0, 1);
    g2.addEdge(1, 2);
    g2.addEdge(2, 3);
    g2.isSC()? cout << "Yes\n" : cout << "No\n";

    return 0;
}

Java

// Java program to check if a given directed graph
// is strongly connected or not with BFS use
import java.util.*;

class Graph {
  int V; // No. of vertices
  // An array of adjacency lists
  ArrayList<ArrayList<Integer> > adj;

  // Constructor and Destructor
  Graph(int V)
  {
    this.V = V;
    adj = new ArrayList<>();
    for (int i = 0; i < V; i++) {
      adj.add(new ArrayList<>());
    }
  }

  // Method to add an edge
  void addEdge(int v, int w)
  {
    adj.get(v).add(w); // Add w to v’s list.
  }

  // A recursive function to print DFS starting from v
  void BFSUtil(int v, boolean visited[])
  {

    // Create a queue for BFS
    Queue<Integer> queue = new ArrayDeque<>();

    // Mark the current node as visited and enqueue it
    visited[v] = true;
    queue.add(v);

    while (!queue.isEmpty())
    {

      // Dequeue a vertex from queue
      v = queue.peek();
      queue.remove();

      // Get all adjacent vertices of the dequeued
      // vertex s If a adjacent has not been visited,
      // then mark it visited and enqueue it
      for (Integer i : adj.get(v)) {
        if (!visited[i]) {
          visited[i] = true;
          queue.add(i);
        }
      }
    }
  }

  // The main function that returns true if the
  // graph is strongly connected, otherwise false
  boolean isSC()
  {
    // Step 1: Mark all the vertices as not
    // visited (For first BFS)
    boolean[] visited = new boolean[V];
    for (int i = 0; i < V; i++)
      visited[i] = false;

    // Step 2: Do BFS traversal starting
    // from first vertex.
    BFSUtil(0, visited);

    // If BFS traversal doesn’t visit all
    // vertices, then return false.
    for (int i = 0; i < V; i++)
      if (visited[i] == false)
        return false;

    // Step 3: Create a reversed graph
    Graph gr = getTranspose();

    // Step 4: Mark all the vertices as not
    // visited (For second BFS)
    for (int i = 0; i < V; i++)
      visited[i] = false;

    // Step 5: Do BFS for reversed graph
    // starting from first vertex.
    // Starting Vertex must be same starting
    // point of first DFS
    gr.BFSUtil(0, visited);

    // If all vertices are not visited in
    // second DFS, then return false
    for (int i = 0; i < V; i++)
      if (visited[i] == false)
        return false;

    return true;
  }

  // Function that returns reverse (or transpose)
  // of this graph
  Graph getTranspose()
  {
    Graph g = new Graph(V);
    for (int v = 0; v < V; v++) {
      // Recur for all the vertices adjacent to this
      // vertex
      for (Integer i : adj.get(v))
        g.adj.get(i).add(v);
    }
    return g;
  }
}

public class GFG {

  // Driver program to test above functions
  public static void main(String[] args)
  {
    Graph g1 = new Graph(5);
    g1.addEdge(0, 1);
    g1.addEdge(1, 2);
    g1.addEdge(2, 3);
    g1.addEdge(3, 0);
    g1.addEdge(2, 4);
    g1.addEdge(4, 2);
    if (g1.isSC())
      System.out.println("Yes");
    else
      System.out.println("No");

    Graph g2 = new Graph(4);
    g2.addEdge(0, 1);
    g2.addEdge(1, 2);
    g2.addEdge(2, 3);
    if (g2.isSC())
      System.out.println("Yes");
    else
      System.out.println("No");
  }
}

// This code is contributed by karandeep1234.

Python3

# Python3 program to check if a given directed graph
# is strongly connected or not with BFS use
from collections import deque

# A recursive function to print DFS starting from v
def BFSUtil(adj, v, visited):

    # Create a queue for BFS
    queue = deque()

    # Mark the current node as visited
    # and enqueue it
    visited[v] = True
    queue.append(v)

    # 'i' will be used to get all adjacent
    # vertices of a vertex
    while (len(queue) > 0):

        # Dequeue a vertex from queue
        v = queue.popleft()
        #print(v)
        #queue.pop_front()

        # Get all adjacent vertices of the
        # dequeued vertex s. If a adjacent
        # has not been visited, then mark it
        # visited and enqueue it
        for i in adj[v]:
            if (visited[i] == False):
                visited[i] = True
                queue.append(i)

    return visited

# Function that returns reverse
# (or transpose) of this graph
def getTranspose(adj, V):

    g = [[] for i in range(V)]

    for v in range(V):

        # Recur for all the vertices adjacent to
        # this vertex
        # list<int>::iterator i
        for i in adj[v]:
            g[i].append(v)

    return g

def addEdge(adj, v, w):

    # Add w to v’s list.
    adj[v].append(w)
    return adj

# The main function that returns True if graph
# is strongly connected
def isSC(adj, V):

    # Step 1: Mark all the vertices as not
    # visited (For first BFS)
    visited = [False]*V

    # Step 2: Do BFS traversal starting
    # from first vertex.
    visited = BFSUtil(adj, 0, visited)
    # print(visited)

    # If BFS traversal doesn’t visit all
    # vertices, then return false.
    for i in range(V):
        if (visited[i] == False):
             return False

    # Step 3: Create a reversed graph
    adj = getTranspose(adj, V)

    # Step 4: Mark all the vertices as not
    # visited (For second BFS)
    for i in range(V):
        visited[i] = False

    # Step 5: Do BFS for reversed graph
    # starting from first vertex.
    # Starting Vertex must be same starting
    # point of first DFS
    visited = BFSUtil(adj, 0, visited)

    # If all vertices are not visited in
    # second DFS, then return false
    for i in range(V):
        if (visited[i] == False):
             return False

    return True

# Driver code
if __name__ == '__main__':

    # Create graphs given in the above diagrams
    g1 = [[] for i in range(5)]
    g1 = addEdge(g1, 0, 1)
    g1 = addEdge(g1, 1, 2)
    g1 = addEdge(g1, 2, 3)
    g1 = addEdge(g1, 3, 0)
    g1 = addEdge(g1, 2, 4)
    g1 = addEdge(g1, 4, 2)
    #print(g1)

    print("Yes" if isSC(g1, 5) else "No")

    g2 = [[] for i in range(4)]

    g2 = addEdge(g2, 0, 1)
    g2 = addEdge(g2, 1, 2)
    g2 = addEdge(g2, 2, 3)

    print("Yes" if isSC(g2, 4) else "No")

# This code is contributed by mohit kumar 29

C#

using System;
using System.Collections.Generic;
using System.Linq;

class Graph
{
    private int V;
    private List<int>[] adj;

    public Graph(int v)
    {
        V = v;
        adj = new List<int>[v];
        for (int i = 0; i < v; i++)
        {
            adj[i] = new List<int>();
        }
    }

    public void addEdge(int v, int w)
    {
        adj[v].Add(w);
    }

    public bool isSC()
    {
        bool[] visited = new bool[V];
        DFSUtil(0, visited);
        for (int i = 0; i < V; i++)
        {
            if (visited[i] == false)
            {
                return false;
            }
        }

        Graph gt = getTranspose();

        for (int i = 0; i < V; i++)
        {
            visited[i] = false;
        }

        gt.DFSUtil(0, visited);
        for (int i = 0; i < V; i++)
        {
            if (visited[i] == false)
            {
                return false;
            }
        }

        return true;
    }

    private void DFSUtil(int v, bool[] visited)
    {
        visited[v] = true;
        for (int i = 0; i < adj[v].Count; i++)
        {
            int n = adj[v][i];
            if (!visited[n])
            {
                DFSUtil(n, visited);
            }
        }
    }

    private Graph getTranspose()
    {
        Graph g = new Graph(V);
        for (int v = 0; v < V; v++)
        {
            for (int i = 0; i < adj[v].Count; i++)
            {
                g.adj[adj[v][i]].Add(v);
            }
        }
        return g;
    }

    public static void Main(string[] args)
    {
        Graph g1 = new Graph(5);
        g1.addEdge(0, 1);
        g1.addEdge(1, 2);
        g1.addEdge(2, 3);
        g1.addEdge(3, 0);
        g1.addEdge(2, 4);
        g1.addEdge(4, 2);

        if (g1.isSC())
            Console.WriteLine("Yes");
        else
            Console.WriteLine("No");

        Graph g2 = new Graph(4);
        g2.addEdge(0, 1);
        g2.addEdge(1, 2);
        g2.addEdge(2, 3);
        if (g2.isSC())
            Console.WriteLine("Yes");
        else
            Console.WriteLine("No");

    }
}

Javascript

<script>
// javascript program to check if a given directed graph
// is strongly connected or not with BFS use


class Graph
{

    constructor(V){
        this.V = V; // No. of vertices
        this.adj = new Array(V); // An array of adjacency lists
        for(let i = 0; i < V; i++){
            this.adj[i] = new Array();
        }
    }

    // A recursive function to print DFS starting from v
    BFSUtil(v, visited)
    {
        // Create a queue for BFS
        let queue = [];

        // Mark the current node as visited and enqueue it
        visited[v] = true;
        queue.push(v);


        while (queue.length > 0)
        {
            // Dequeue a vertex from queue
            v = queue[0];
            queue.shift();

            // Get all adjacent vertices of the dequeued vertex s
            // If a adjacent has not been visited, then mark it
            // visited and enqueue it
            for (let i = 0; i < this.adj[v].length; i++)
            {
                let x = this.adj[v][i];
                if (!visited[x])
                {
                    visited[x] = true;
                    queue.push(x);
                }
            }
        }
    }

    // Function that returns reverse (or transpose) of this graph
    getTranspose()
    {
        let g = new Graph(this.V);
        for (let v = 0; v < this.V; v++)
        {
            // Recur for all the vertices adjacent to this vertex
            for (let i = 0; i < this.adj[v].length; i++){
                let x = this.adj[v][i];
                g.adj[x].push(v);
            }
        }
        return g;
    }

    addEdge(v, w)
    {
        this.adj[v].push(w); // Add w to v’s list.
    }

    // The main function that returns true if graph
    // is strongly connected
    isSC()
    {
        // Step 1: Mark all the vertices as not
        // visited (For first BFS)
        let visited = new Array(this.V);
        for (let i = 0; i < this.V; i++)
            visited[i] = false;

        // Step 2: Do BFS traversal starting
        // from first vertex.
        this.BFSUtil(0, visited);

        // If BFS traversal doesn’t visit all
        // vertices, then return false.
        for (let i = 0; i < this.V; i++)
            if (visited[i] == false)
                 return false;

        // Step 3: Create a reversed graph
        let gr = this.getTranspose();

        // Step 4: Mark all the vertices as not
        // visited (For second BFS)
        for(let i = 0; i < this.V; i++)
            visited[i] = false;

        // Step 5: Do BFS for reversed graph
        // starting from first vertex.
        // Starting Vertex must be same starting
        // point of first DFS
        gr.BFSUtil(0, visited);

        // If all vertices are not visited in
        // second DFS, then return false
        for (let i = 0; i < this.V; i++)
            if (visited[i] == false)
                 return false;

        return true;
    }

};



// Driver program to test above functions
// Create graphs given in the above diagrams
let g1 = new Graph(5);
g1.addEdge(0, 1);
g1.addEdge(1, 2);
g1.addEdge(2, 3);
g1.addEdge(3, 0);
g1.addEdge(2, 4);
g1.addEdge(4, 2);
if(g1.isSC()){
    document.write("Yes");
}
else{
    document.write("No");
}

let g2 = new Graph(4);
g2.addEdge(0, 1);
g2.addEdge(1, 2);
g2.addEdge(2, 3);
if(g2.isSC()){
    document.write("Yes");
}
else{
    document.write("No");
}

// the code is contributed by Nidhi goel.
</script>

Output

Yes
No

Time Complexity: Time complexity of above implementation is same as Breadth First Search which is O(V+E) if the graph is represented using adjacency matrix representation.

Can we improve further?
The above approach requires two traversals of graph. We can find whether a graph is strongly connected or not in one traversal using Tarjan’s Algorithm to find Strongly Connected Components.

This article is contributed by Shivam Pradhan. If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.