Stoke’s Law: Observe a raindrop falling from a height if you look closely you will notice that the speed of all the raindrops is constant and even though it falls from a height under the influence of gravity its velocity seems constant. These questions are answered using Stoke’s law
Stoke’s law was first proposed by the famous English scientist George Gabriel Stokes. This law tells us that the velocity of any object increases gradually when it is dropped in any medium until it reaches a constant velocity then that object proceeds without changing its velocity.
This article will explore Stoke’s law, its definition, formula, examples, applications, conditions, etc.
What is Stoke’s Law?
Stoke’s Law is an equation that expresses the velocity of small spherical particles in a fluid medium. The law is established by taking into account the forces acting on a certain particle as it falls through a liquid column under the influence of gravity.
Stoke’s Law Definition
Stokes Law state that, “There is a drag force working on the spherical body which is following in a column and the upward drag force on the body ultimately equals the gravitational force then the body drops with a constant velocity.”
The force that retards a sphere passing through a viscous fluid is directly proportional to the sphere’s velocity, radius, and fluid viscosity. Sir George G. Stokes, an English physicist, stated the viscous drag force acts on a body dropping in a liquid, this force is denoted using the letter ‘F’.
Stoke’s Law Mathematical Expression
In Stokes’s law, the drag force F acting upward in resistance to the fall is equal to 6πrηv, in which r is the radius of the sphere, η is the viscosity of the liquid, and v is the velocity of the fall.
F=6πηrv
Where:
- F is the drag force acting on the object,
- η (Greek letter eta) is the dynamic viscosity of the fluid,
- r is the radius of the spherical object, and
- v is the velocity of the object relative to the fluid.
Stokes’s law gives us a mathematical equation that tells us about the drag force acting on a spherical particle when passing through a liquid under the influence of gravity. Stokes Law Formula is stated as,
F = 6πηrv
where
F is the frictional force
η is the viscosity of the liquid
r is the radius
v is the velocity of the flow
Importance of Stoke’s Law
Following are the importance of Stoke’s Law:
- Millikan employs this rule in his oil-drop experiment to determine the electric charge.
- Working of a parachute is based on the principle of Stoke’s Law.
- Cloud formation and floating are explained using Stoke’s Law.
Stoke’s Law Derivation
The viscous force acting on a sphere is directly proportional to the following factors:
Coefficient of viscosity (η) as F ∝ ηa …(i)
Radius of the sphere (r) as F ∝ rb …(ii)
Velocity of the object (v) as F ∝ vc …(iii)
Combining the above three equations we get,
F ∝ ηa rb vc
Removing the proportionality sign and adding the proportionality constant k we get.
F = k ηa rb vc……(1)
Now, equating the dimensions of parameters on either side of equation (1)
[MLT–2] = [ML–1T–1]a [L]b [LT-1]c
Simplifying the above equation,
[MLT–2] = [Ma ⋅ L–a+b+c ⋅ T–a–c]……(2)
Equating the superscripts of mass, length, and time respectively from equation (2), we get
a = 1 ….(a)
–a + b + c = 1 ……(b)
–a –c = 2
a + c = 2 ……(c)
from (b), (c)
1 + c = 2
c = 1 ……(d)
from (a) & (b) in (d), we get
–1 + b + 1 = 1
b = 1 ……(e)
from (a), (d), and (e)
F = k η r v
For any spherical body, the value of k was experimentally obtained to be 6π.
Thus, the viscous force on a spherical body falling through a liquid is given by the equation,
F = 6πηrv
Hence, this is the required relation of Stoke’s Law.
Limitations of Stoke’s Law
Various limitations of Stoke’s Law are discussed below in the article,
Negative Density Difference in Stoke’s Equation
Stokes’ equation is invalid if the density difference in the equation is negative that is when the particles are lighter than the dispersion medium. This results in floatation or creaming most commonly seen in emulsion systems.
High Content of Dispersed Solids
When the solid content of a suspension is high, Stokes’ equation may not show the real sedimentation rate. High solid content imparts additional viscosity to the system, which must be taken into consideration if the correct rate of settling is to be determined. The equation contains only the viscosity of the medium.
Dielectric Constant
The dielectric constant, which is not used in Stokes’ equation, is a significant parameter in many contexts. The electrical potential between two charges is inversely proportional to the medium’s dielectric constant. As a result, the zeta potential is affected by the medium’s dielectric constant. The assumption is that if an automobile has a low dielectric constant, the double layer is several times thicker than in an aqueous medium, resulting in different zeta potential and, therefore, a different setting. These considerations are critical for using non-aqueous vehicles such as sesame oil, corn oil, and chlorofluorocarbon propellant (in aerosol suspension).
Brownian Movement
Another aspect that can affect the precision of Stokes’ equation results is Brownian movement, which is a spontaneous (zigzag) movement of particles floating in a fluid caused by collisions with fast-moving atoms or molecules in the gas or liquid. Sedimentation is mitigated to some degree by Brownian migration. This results in a significant difference between the real rate of sedimentation and the rate measured using Stokes’ equation.
Conditions for Stoke’s Law
Conditions under which Stoke’s Law is valid are,
- The fluid through which the body moves must have an infinite extension.
- The body is perfectly rigid and smooth.
- There is no slip between the body and the fluid. The motion of the body does not give rise to turbulent motion. Hence, the motion is streamlined.
- The size of the body is small, but it is larger than the distance between the molecules of the liquid. Thus, the medium is homogeneous and continuous for such a body.
Applications of Stoke’s Law in Real Life
Velocity of Raindrops
Raindrops do not reach extremely high speeds during their free fall. If this does not occur, a person walking in the rain will be injured. This is because the viscous drag in air opposes the velocity of raindrops as they descend due to gravity. The drop reaches a terminal velocity when the viscous force equals the force of gravity. As a result, raindrops reaching the earth have low kinetic energy.
Parachute
When we jump out of an aeroplane, a parachute assists us in landing safely on the ground. Because in this case, the person falls with g acceleration due to gravity, but the acceleration decreases due to viscous drag in the air until the person attains terminal velocity. The person then drops at a constant speed and opens his parachute close to the ground at a predetermined period, allowing him to land safely near his destination.
It is used to calculate the charge of an electron. (The oil drop method of Millikan)
Terminal Velocity
When a body falls through a viscous fluid, it produces relative motion between its different layers. As a result, the body experiences a viscous force that tends to retard its motion. As the velocity of the body increase, the viscous force (F = 6 π η r v) also increases. A stage is reached when the weight of the body becomes just equal to the sum of the upthrust and viscous force. Then no net force acts on the body, and it begins to move with a constant velocity. So, here comes the concept of Terminal Velocity.
The maximum constant velocity acquired by a body while falling through a viscous medium is called its Terminal Velocity.
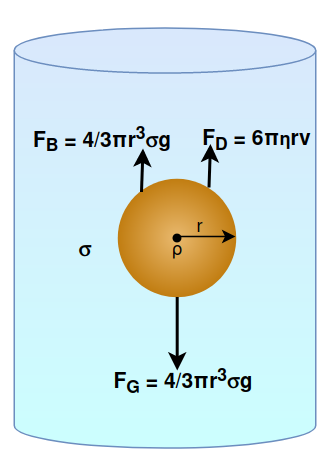
As the speed of an object increases, so does the drag force acting on it, which also depends on the substance it is passing through (for example air or water). At some speed, the drag or force of resistance will equal the gravitational pull on the object (buoyancy is considered below). At this point, the object stops accelerating and continues falling at a constant speed called the terminal velocity (also called settling velocity).
Terminal Velocity Formula
The formula for terminal velocity (vt) is,
vt = 2r2 × (ρ−σ)g / 9η
where
ρ is the mass density of the sphere
σ is the mass densities of the fluid
r is the radius of the raindrop
Read More,
Stoke’s Law Examples
Example 1: A raindrop of radius 0.3 mm falls through the air with a terminal velocity of 1 m/s. The viscosity of air is 18 × 10-5 Poise. Find the viscous force on the raindrop.
Solution:
Given,
Radius of the raindrop, r = 0.3mm = 0.03 cm.
Terminal velocity, v = 1 m/s =100 cm/s.
Viscosity of air, η = 18 × 10-5 Poise.
According to Stokes law, force of viscosity on rain drop is
F = 6π η r v
= 6 × 3.142 × 18 × 10-5 Poise × 0.03 cm × 100 cm/s
= 1.018 × 10-2 dyne
Example 2: A solid metal ball falling in a liquid column attains a terminal velocity of 3 m/s. Find the viscosity of the liquid if the radius of the ball is r = 7 cm and its density is dl = 1000kg/m3 and the density of the metal ball is ds = 7050 kg/m3 (Take g = 10 m/s2)
Solution:
Given,
Radius of Sphere r = 3 cm = 0.03 m
Density of Sphere ds = 7050 kg/m3
Density of liquid dl = 1000 kg/m3
Terminal Velocity = 5 m/s
vt = 2r2 × (ρ−σ)g / 9η
Substituting the values in the terminal velocity equation,
3 = 2(0.03)2 × (7050 -1000)10 / 9η
3 = (6×10-4 × 60500) / 9η
3 = 36.3/9η
9η = 12.1
η = 12.1/9 = 1.344 kg/ms
Example 3: The speed of water in a water stream is 18 km/h near the surface. If the stream is 10 m deep, then determine the Shearing stress between the surface layer and the bottom layer (coefficient of viscosity of water, η=10−3 Pa s).
Solution:
Since, velocity of water at the bottom of the river is 0 m/s,
Therefore, dv = 18 km/h = (18 × 5/18) m/s = 5 m/s
Also, dx = 10 m and η=10−3 Pa s
Force of viscosity, F = η A (dv/dx)
Therefore,
Shearing stress = F / A = η (dv/dx)
= 10−3 Pa s × (5 m/s / 10 m)
= 5 ×10−2 N m-2
Summary – Stoke’s Law
Stoke’s Law is like a guidebook explaining why objects like raindrops fall at a steady speed instead of speeding up non-stop. Proposed by George Gabriel Stokes, this law dives into the world where tiny spherical objects slow dance with fluids, revealing why they eventually settle into a graceful, constant descent. Picture a raindrop tumbling down, initially picking up speed due to gravity’s pull. According to Stoke’s Law, as it falls, the liquid around it starts to push back, gradually increasing until this push matches gravity’s pull. When these forces balance out, our raindrop glides smoothly at a constant pace, hitting the ground gently instead of with a splash. This isn’t just about raindrops; Stoke’s Law has its fingers in many pies, from parachutes fluttering to safety, clouds wafting across the sky, to the nitty-gritty of scientific experiments like measuring an electron’s charge. It’s a fascinating peek into how objects interact with the world on a microscopic level, transforming seemingly chaotic descents into harmonious falls.
FAQs on Stokes law
Define Stoke’s Law
The equation which gives the drag force acting on the body if it is in free fall in any liquid column is called Stoke’s Law. It is used to find the terminal velocity of an object.
When do we use Stoke’s Law?
Stoke’s Law is used to determine the terminal velocity of any object. This law also works in explaining the working of parachutes, cloud formation and others.
When is Stoke’s Law valid?
Stoke’s Law is valid only when the velocity of the object is constant under influence of the gravitational force which is balanced by the drag force of the liquid.
What are the Applications of Stoke’s Law?
Various applications of Stoke’s Law are,
- Measuring the Viscosity of Fluid
- Finding the Terminal Velocity of an object, etc.
What is the Force on the Water Drop falling with a Constant Velocity?
When a drop falls at a constant velocity, the viscous force is balanced by its weight i.e. the force of gravity. Therefore, the resulting force is zero.
What is Terminal Velocity?
Terminal velocity is the velocity of an object when the net force acting on the object is zero. In the case of raindrops, the mass of the drop acts downward while the viscous force of the air acts upward when these two force balance each other the velocity attained by the raindrop is called the Terminal Velocity.
Share your thoughts in the comments
Please Login to comment...