As liquid runs into a channel, it collides with the pipe. Engineers ensure that the liquid flow through the city’s pipes is as consistent as possible. As a result, a number known as the Reynolds number predicts whether the flow of the liquid will be smooth or turbulent. Sir George Stoke was the first to introduce this concept. Later, it was popularised by Osborne Reynolds, and the number was dubbed the Reynolds number. The Reynolds number is a pure number that specifies how much liquid flows into a vessel. Because air and liquids move, they are fluids, and their movement is flow. In addition, we will look at a fluid flow parameter known as the Reynolds number, as well as the Reynolds Number Formula, in this topic. Whether the fluid is turbulent or laminar is determined by its value.
Reynolds Number
It is the ratio of an inertia force to the viscous force of a fluid. Furthermore, the inertia force is the momentum force of the mass of a flowing stream. It is a measure of how difficult it would be to adjust the velocity of a moving stream in basic terms. The viscous force, on the other hand, is the force that deals with the friction of a flowing fluid. Furthermore, the inertial and viscous forces are very comparable. In addition, they share the same unit, implying that the Reynolds number is unit less.
The Reynolds number is a dimensionless quantity that determines whether a flow pattern is laminar or turbulent as it passes through a pipe. The ratio of inertial forces to viscous forces determines the Reynolds number.
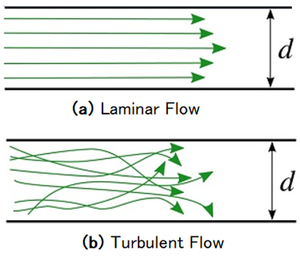
In everyday life, the Reynolds number has a variety of potentials. It can be used to describe liquid flow in a pipe, airfoil flow, or an object moving through a fluid. Laminar flow is a type of fluid flow in which the fluid flows smoothly and in predictable patterns. Turbulent flow, on the other hand, is irregular in nature and involves a lot of mixing.
Reynolds Number Formula
The formula for the Reynolds number is given as:
Re = (pVD) / u
Here,
Re is the Reynolds number, p is the density of fluid, V is the velocity of flow, D is the diameter of pipe and u is the viscosity of the fluid.
The flow through the pipe is said to be turbulent if the computed Reynolds number is high. The flow is said to be laminar if the Reynolds number is low. These are acceptable numerical values, while laminar and turbulent flows are often grouped within a range. Laminar flow has a Reynolds number less than 2000, while turbulent flow has a Reynolds number greater than 2000.
Sample Problems
Problem 1: Determine the flow of fluid having a relative density of 100 kg/m3, the viscosity of 0.5 Ns/m2 with a velocity of 5 m/s through a pipe of 0.2 m.
Solution:
The type of flow can be determined by the value of Reynolds number.
Given:
Velocity of fluid, V=5 m/s
Diameter of pipe, D= 0.2 m
Relative density of fluid, p=100 kg/m^3
Viscosity of fluid=0.5 Ns/m^2
The formula of Reynolds number is given as:
Re = pVD/u
Substitute all the values in the formula to calculate the Reynolds number.
Re = (100 kg/m3)(5 m/s)(0.2 m)/(0.5 Ns/m2)
= 200
Since, the Reynolds number is less than 2000, the flow of liquid is laminar.
Problem 2: Let’s suppose we’re conducting study on water flowing via pipes. We’d also like to compare the diameters of the two pipes that demonstrate laminar flow, which is when water flows smoothly in a straight line.
Moreover, pipes with turbulent flow, in which water flows in a chaotic manner, make flow predictions challenging. It can also generate vibration, which can eventually cause wear and tear in the flow system, resulting in its failure.
The water passing through the two separate pipes should have a Reynolds number of 2200 in our research paper. The first pipe in this set has a diameter of 2.75 cm (0.0275 m). In addition, water has a density of 1,000 Kg/m^3. Above all, water has a viscosity of 0.0013 kg/(ms). Calculate the water’s velocity through the pipe to meet those standards.
Solution:
The formula of Reynolds number is given as:
Re = pVD/u
Substitute the given values to find out the velocity.
2200 = (1000 kg/m3)(0.0275 m)V/(0.00133 Pa⋅ s)
V ≈ 0.11 ms
Now we must use various pipes of various sizes with the same configuration, as well as compute the water velocity that must travel through it. Furthermore, when the water is running through the pipe at a calculated velocity, we will add a dye to it.
Also, if the dye water shows laminar flow, we’ve demonstrated how dynamic similitude works. Let’s finish the computation to estimate the water velocity that should flow through a smaller pipe.
Consider the pipe diameter be 0.005 m.
2200=(1000 kg/m3)(0.005 m)V/(0.00133 Pa⋅s)
V ≈ 0.59 ms
We arrive at the conclusion that water in a smaller pipe flows quicker than water in a larger conduit after the calculations. Also, because the Reynolds number is the same as in the preceding example, even when the water in the smaller pipe flows faster, the water still flows in a laminar pattern.
Problem 3: What should be the Reynolds number for laminar flow?
Answer:
The fluid particles in laminar flow move in unmixing layers or streams that follow a smooth continuous course. The Reynolds number should be less than 2000 for laminar flow.
Problem 4: What should be the Reynolds number for turbulent flow?
Answer:
The motion of fluid particles in turbulent flow is uneven, and it follows erratic and unpredictable patterns. The Reynolds number should be more than 2000 for turbulent flow.
Problem 5: Calculate the Reynolds number, Re, for oil flow in a circular pipe. The diameter of the pipe is 60 mm, the density of the oil is 910 kg/m3, the volumetric oil flow rate is 60 L/min, and the dynamic viscosity of the oil is 50 m Pa s.
Solution:
Given:
Diameter of the pipe, D = 60 mm = 0.06 m.
Density of the oil, p = 910 kg/m3
Volume flow rate, Q = 60 L/min = 0.01 m3/s.
Dynamic viscosity, u=50 m Pa s =0.05 Pa s
The area of the pipe is given as:
A = π(D/2)2
= π(0.06/2)2
= 0.0283 m2
The formula for volume flow rate is given as:
Q = Av
0.01 = 0.0283 × V
V = 0.353 m/s
The formula of Reynolds number is given as:
Re = pVD/u
Substitute all the values to find the Reynolds number.
Re = (910 kg/m3)(0.353 m/s)(0.06 m)/(0.05 Pa s)
= 386
Thus, the Reynolds number of the flow is 386.
Share your thoughts in the comments
Please Login to comment...