Every physical occurrence in the universe of physics includes some type of attraction or repulsion, which causes the universe to exist in a unique way. The environment remains in a well-equipped and well-balanced state due to the attraction and repulsions between particles. When these attractions and repulsions are manipulated to disturb or vary, the outcomes in observations can be remarkable.
Consider an atom’s electrons: if the attraction between protons in the nucleus and electrons in the shells is disrupted, the atom can be destroyed. Physicists have long been fascinated by the quantitative side of physics since it aids in the understanding of concepts and the development of new theories and ideas.
In 1785, a French physicist named Charles Augustin de Coulomb coined a measurable mathematical relationship between two electrically charged bodies. Coulomb’s law, often known as Coulomb’s inverse-square law, is an equation that helps to determine the extent of repulsion or attraction force between two charged particles.
Coulomb’s Law
Coulomb’s Law describes the force that exists between two point charges. The term point charge refers to the fact that the size of linearly charged objects is relatively small in comparison to the distance between them in physics. As a result, we treat them as point charges since calculating the force of attraction/repulsion between them is simple.
Therefore, Coulomb’s Law can be stated as:
The force of attraction or repulsion between two charged bodies is directly proportional to the product of their charges and inversely proportional to the square of the distance between them, according to Coulomb’s law. It acts on the line that connects the two charges that are called point charges.
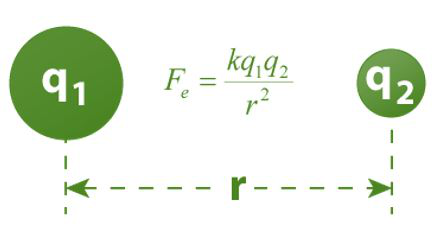
Pictorial Representation for Coulomb’s Law
In general, the statement has two charges, q1 and q2. The attraction/repulsion force between the charges is ‘F’, and the distance between them is ‘r’. Then mathematically Coulomb’s law is given as:
- The electrostatic force, F is directly proportional to the product of the magnitude of the charges in contact i.e. F ∝ q1q2
- The electrostatic force, F is inversely proportional to the square of the distance between the two charges in contact i.e. F ∝ 1/r2
Let’s combine the above to relation as
F ∝ q1q2 / r2
Now, introduce a new proportionality constant k as,
F = k q1q2 / r2
where k is proportionality constant and equals 1/4πε0, here ε0 is called epsilon not which indicates the permittivity of a vacuum. The calculated value of k is 9 × 109 Nm2/ C2.
Like charges repel one other, while unlike charges attract each other, according to Coulomb. This means that charges of the same sign will repel each other, while charges of opposite signs will attract each other.
Coulomb’s Law in Vector Form
There are two sorts of physical quantities: Scalars (with just one magnitude) and Vectors (with many magnitudes) (those quantities with magnitude and direction). Because it has both magnitude and direction, force is a vector quantity. In the form of vectors, Coulomb’s law can be rewritten. Remember that the vector “F” is denoted as 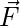 , and the vector “r” is denoted as
, and the vector “r” is denoted as 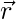 , and so on.
, and so on.
Let’s say there are two charges, q1 and q2, with r1 and r2 as their location vectors. Because both charges are of the same sign, a repulsive force will exist between them. Let F12 be the force on the q1 charge due to q2, and F21 be the force on the q2 charge due to the q1 charge. The r21 vector is the matching vector from q1 to q2.
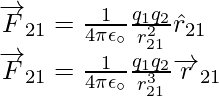
When using Coulomb’s Law to calculate the force between two point charges, keep the following points in mind. Because both charges are inherently opposite, the vector form of the equation is unaffected by their signs.
Owing to the change in position vector, the repulsive force F21, which is the force on charge q1 due to q2, and another repulsive force F21, which is the force on charge q2 due to q1, have opposite signs.
F12 = – F21
This is due to the fact that the position vector for force F12 is r12, while the position vector for force F21 is r21.
r21 = r2 – r1
and
r12 = r1 – r2
Because the signs of r21 and r12 are opposed, they produce forces with opposing signs. This demonstrates that Coulomb’s Law is compatible with Newton’s Third Law, which states that every action has an equal and opposite reaction. When two charges are present in a vacuum, Coulomb’s Law determines the force between them. This is due to the fact that in a vacuum, charges are unaffected by other matter or particles.
Limitations of Coulomb’s Law
Coulomb’s Law is based on a set of assumptions and cannot be employed in the same way as other universal formulas. The following points are covered by the law:
- If the charges are static, we can utilise the formula (in rest position)
- When dealing with charges that have a normal and smooth shape, the formula is simple to employ; but, when dealing with charges that have irregular shapes, it becomes too complicated.
- Only when the solvent molecules between the particles are significantly larger than both charges is the formula valid.
Problems Based on Coulomb’s Law
Problem 1: What will be the electrostatic force between the two-point charges of charges +2μC and +4μC repel each other with a force of 20N when a charge of −6μC is added to each of them?
Solution:
Given that,
The first charge, q1 is +2μC.
The second charge, q2 is +4μC.
The third charge, q3 is -6μC.
The electrostatic force in the first case, F is 20 N.
Therefore,
F = k q1q2 / r2
or
20 N = k (+2μC × +4μC) / r2 …… (1)
Now, when a third charge q3 is introduces to q1 and q2 then, charges on both q1 and q2 changes as:
q1′ = (2 – 6) μC = -4 μC
q2′ = (4 – 6) μC = -2 μC
Then, the electrostatic force in this new case is:
F’ = k q’1q’2 / r2
= k (-4 μC × -2 μC) / r2 …… (2)
Now, in order to obtain F’, lets divide equation (2) by (1) as,
F’ / 20 N = [k (-4 μC × -2 μC) / r2] / [20 N = k (+2μC × +4μC) / r2 ]
F’ = +20 N
Hence, the electrostatic force when third charge is introduced is +20 N.
Problem 2: Determine the electrostatic force between the two charges of magnitude 2 C and -1 C separated by a distance 1m in air.
Solution:
Given that,
The first charge, q1 is +2 C.
The second charge, q2 is -1C.
The distance between the two charges, r is 1 m.
The formula to calculate electrostatic force between the charges is:
F = k q1q2 / r2
Substitute the given values in the above expression as,
F = (9 × 109 Nm2/ C2)(+2 C)(-1 C) / (1 m)2
= 18 × 109 N
Problem 3: The distance between the two electrons in contact is equal to 1Å. Determine the Coulomb force between them.
Solution:
The charge on an electron, q is -1.6 × 10-19 C.
The distance between the two charges, r is 1 Å.
The formula to calculate electrostatic force between the two electrons is:
F = k (q2 / r2)
Substitute the given values in the above expression as,
F = (9 × 109 Nm2/ C2) [(-1.6 × 10-19 C)2 / (1 Å)2]
= 2.3 × 10−8 N
Problem 4: When held apart at a certain distance, two spherical conductors B and C with similar radii and carrying equal charges repel each other with a force F. A third spherical conductor, with the same radius as B but no charge, is brought into contact with B, then with C, and ultimately removed from both. What is the new repulsion force between B and C?
Solution:
For the given case,
Initially the electrostatic force on the conductors is defined as:
F = k (q2 / r2) ……(1)
But when a third spherical conductor comes in contact alternately with B and C then removed, so charges on B and C are Q / 2 and 3Q / 4 respectively.
Therefore, the New force becomes as:
F’ = k [Q / 2) (3Q / 4)/ r2] ……(2)
Comparing equation (1) and (2), we get:
F’ = 38F
Problem 5: Consider a system of two charges of magnitude 2 × 10-7 C and 4.5 × 10-7 C which is acted upon by a force of 0.1 N. What is the distance between the two charges?
Solution:
Given that,
The first charge, q1 is 2 × 10-7 C.
The second charge, q2 is 4.5 × 10-7 C.
The force acted upon them, F is 0.1 N.
The formula to calculate electrostatic force between the charges is:
F = k q1q2 / r2
Substitute the given values in the above expression as,
0.1 N = (9 × 109 Nm2/ C2)(2 × 10-7 C)(4.5 × 10-7 C) / (r)2
r = 0.09 m
Hence, the distance between the two charges, r is 0.9 m.
Problem 6: Determine the magnitude of the two identical charges, when the electrostatic force between these two identical charges is 1000 N and are separated by a distance of 0.1 m.
Solution:
Given that,
The distance between the two charges, r is 0.1 m.
The force acted upon them, F is 1000 N.
The formula to calculate electrostatic force between the charges is:
F = k q2 / r2
where q is the charge.
Rearrange the above formula for q as,
q2 = Fr2 / k
Substitute the given values in the above expression as,
q2 = (1000 N) (0.1 m)2 / (9 × 109 Nm2/ C2)
q = 0.33 × 10-5 C
Hence, the magnitude of the charge is 0.33 × 10-5 C.
Problem 7: Consider two opposite charges with the same magnitude, placed at a distance from each other such that the force of F N acts between these two charges. If 60% of the charge from one is transferred to another. Determine how much the value of force changes in this case.
Solution:
Initially, the electrostatic force between the two charges is given by,
F = k q2 / r2 ……(1)
Now, when the charge is transferred, the electrostatic force becomes,
F’ = k q1q2 / r2 ……(2)
The transferred charge is,
60 % of q = 60 / 100 × q = 3 / 5 q
Therefore, charge q1 = q – 3 / 5 q
= 2 / 5 q
And the charge q2 = q + 3 / 5 q
= 8 / 5 q
Thus, the net force between these charges is,
F’ = k q1q2 / r2
= k (2 / 5 q) (8 / 5 q) / r2
= 16 / 25 F
Problem 8: A specific charge Q is split into two components, q, and Q-q. What is the relation between Q and q if the two portions are separated by r and have the greatest Coulomb repulsion?
Solution:
Given that, the given charge Q is divided into charges Q-q and q separated by a distance r.
We know,
F = k q1q2 / r2
i.e.
F = k q (Q-q) / r2
Now, to maximize this force lets take:
d F / d q = 0
which implies,
(Q-q) – q = 0
2 q =Q
or
q = Q / 2
Share your thoughts in the comments
Please Login to comment...