Reverse Delete Algorithm for Minimum Spanning Tree

Reverse Delete algorithm is closely related to Kruskal’s algorithm. In Kruskal’s algorithm what we do is : Sort edges by increasing order of their weights. After sorting, we one by one pick edges in increasing order. We include current picked edge if by including this in spanning tree not form any cycle until there are V-1 edges in spanning tree, where V = number of vertices.

In Reverse Delete algorithm, we sort all edges in decreasing order of their weights. After sorting, we one by one pick edges in decreasing order. We include current picked edge if excluding current edge causes disconnection in current graph. The main idea is delete edge if its deletion does not lead to disconnection of graph.

The Algorithm :

1. Sort all edges of graph in non-increasing order of edge weights.
2. Initialize MST as original graph and remove extra edges using step 3.
3. Pick highest weight edge from remaining edges and check if deleting the edge disconnects the graph   or not.
    If disconnects, then we don’t delete the edge.
   Else we delete the edge and continue. 

Illustration:

Let us understand with the following example:

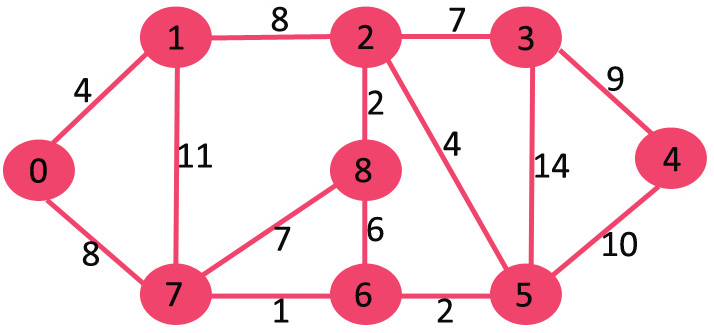
If we delete highest weight edge of weight 14, graph doesn’t become disconnected, so we remove it. 

Next we delete 11 as deleting it doesn’t disconnect the graph. 

Next we delete 10 as deleting it doesn’t disconnect the graph. 

Next is 9. We cannot delete 9 as deleting it causes disconnection. 

We continue this way and following edges remain in final MST. 

Edges in MST
(3, 4) 
(0, 7) 
(2, 3) 
(2, 5) 
(0, 1) 
(5, 6) 
(2, 8) 
(6, 7) 

Note : In case of same weight edges, we can pick any edge of the same weight edges.

Implementation:

C++

// C++ program to find Minimum Spanning Tree
// of a graph using Reverse Delete Algorithm
#include<bits/stdc++.h>
using namespace std;

// Creating shortcut for an integer pair
typedef  pair<int, int> iPair;

// Graph class represents a directed graph
// using adjacency list representation
class Graph
{
    int V;    // No. of vertices
    list<int> *adj;
    vector< pair<int, iPair> > edges;
    void DFS(int v, bool visited[]);

public:
    Graph(int V);   // Constructor

    // function to add an edge to graph
    void addEdge(int u, int v, int w);

    // Returns true if graph is connected
    bool isConnected();

    void reverseDeleteMST();
};

Graph::Graph(int V)
{
    this->V = V;
    adj = new list<int>[V];
}

void Graph::addEdge(int u, int v, int w)
{
    adj[u].push_back(v); // Add w to v’s list.
    adj[v].push_back(u); // Add w to v’s list.
    edges.push_back({w, {u, v}});
}

void Graph::DFS(int v, bool visited[])
{
    // Mark the current node as visited and print it
    visited[v] = true;

    // Recur for all the vertices adjacent to
    // this vertex
    list<int>::iterator i;
    for (i = adj[v].begin(); i != adj[v].end(); ++i)
        if (!visited[*i])
            DFS(*i, visited);
}

// Returns true if given graph is connected, else false
bool Graph::isConnected()
{
    bool visited[V];
    memset(visited, false, sizeof(visited));

    // Find all reachable vertices from first vertex
    DFS(0, visited);

    // If set of reachable vertices includes all,
    // return true.
    for (int i=1; i<V; i++)
        if (visited[i] == false)
            return false;

    return true;
}

// This function assumes that edge (u, v)
// exists in graph or not,
void Graph::reverseDeleteMST()
{
    // Sort edges in increasing order on basis of cost
    sort(edges.begin(), edges.end());

    int mst_wt = 0;  // Initialize weight of MST

    cout << "Edges in MST\n";

    // Iterate through all sorted edges in
    // decreasing order of weights
    for (int i=edges.size()-1; i>=0; i--)
    {
        int u = edges[i].second.first;
        int v = edges[i].second.second;

        // Remove edge from undirected graph
        adj[u].remove(v);
        adj[v].remove(u);

        // Adding the edge back if removing it
        // causes disconnection. In this case this
        // edge becomes part of MST.
        if (isConnected() == false)
        {
            adj[u].push_back(v);
            adj[v].push_back(u);

            // This edge is part of MST
            cout << "(" << u << ", " << v << ") \n";
            mst_wt += edges[i].first;
        }
    }

    cout << "Total weight of MST is " << mst_wt;
}

// Driver code
int main()
{
    // create the graph given in above figure
    int V = 9;
    Graph g(V);

    //  making above shown graph
    g.addEdge(0, 1, 4);
    g.addEdge(0, 7, 8);
    g.addEdge(1, 2, 8);
    g.addEdge(1, 7, 11);
    g.addEdge(2, 3, 7);
    g.addEdge(2, 8, 2);
    g.addEdge(2, 5, 4);
    g.addEdge(3, 4, 9);
    g.addEdge(3, 5, 14);
    g.addEdge(4, 5, 10);
    g.addEdge(5, 6, 2);
    g.addEdge(6, 7, 1);
    g.addEdge(6, 8, 6);
    g.addEdge(7, 8, 7);

    g.reverseDeleteMST();
    return 0;
}

Java

// Java program to find Minimum Spanning Tree
// of a graph using Reverse Delete Algorithm
import java.util.*;

// class to represent an edge
class Edge implements Comparable<Edge> {
  int u, v, w;
  Edge(int u, int v, int w)
  {
    this.u = u;
    this.w = w;
    this.v = v;
  }
  public int compareTo(Edge other)
  {
    return (this.w - other.w);
  }
}
// Class to represent a graph using adjacency list
// representation
public class GFG {

  private int V; // No. of vertices
  private List<Integer>[] adj;
  private List<Edge> edges;
  @SuppressWarnings({ "unchecked", "deprecated" })
  public GFG(int v) // Constructor
  {
    V = v;
    adj = new ArrayList[v];
    for (int i = 0; i < v; i++)
      adj[i] = new ArrayList<Integer>();
    edges = new ArrayList<Edge>();
  }

  // function to Add an edge
  public void AddEdge(int u, int v, int w)
  {
    adj[u].add(v); // Add w to v’s list.
    adj[v].add(u); // Add w to v’s list.
    edges.add(new Edge(u, v, w));
  }

  // function to perform dfs
  private void DFS(int v, boolean[] visited)
  {
    // Mark the current node as visited and print it
    visited[v] = true;
    // Recur for all the vertices adjacent to
    // this vertex
    for (int i : adj[v]) {
      if (!visited[i])
        DFS(i, visited);
    }
  }
  // Returns true if given graph is connected, else false
  private boolean IsConnected()
  {
    boolean[] visited = new boolean[V];
    // Find all reachable vertices from first vertex
    DFS(0, visited);
    // If set of reachable vertices includes all,
    // return true.
    for (int i = 1; i < V; i++) {
      if (visited[i] == false)
        return false;
    }
    return true;
  }

  // This function assumes that edge (u, v)
  // exists in graph or not,
  public void ReverseDeleteMST()
  {
    // Sort edges in increasing order on basis of cost
    Collections.sort(edges);
    int mst_wt = 0; // Initialize weight of MST
    System.out.println("Edges in MST");
    // Iterate through all sorted edges in
    // decreasing order of weights
    for (int i = edges.size() - 1; i >= 0; i--) {
      int u = edges.get(i).u;
      int v = edges.get(i).v;
      // Remove edge from undirected graph
      adj[u].remove(adj[u].indexOf(v));
      adj[v].remove(adj[v].indexOf(u));

      // Adding the edge back if removing it
      // causes disconnection. In this case this
      // edge becomes part of MST.
      if (IsConnected() == false) {
        adj[u].add(v);
        adj[v].add(u);
        // This edge is part of MST
        System.out.println("(" + u + ", " + v
                           + ")");
        mst_wt += edges.get(i).w;
      }
    }
    System.out.println("Total weight of MST is "
                       + mst_wt);
  }
  // Driver code
  public static void main(String[] args)
  {
    // create the graph given in above figure
    int V = 9;
    GFG g = new GFG(V);
    // making above shown graph
    g.AddEdge(0, 1, 4);
    g.AddEdge(0, 7, 8);
    g.AddEdge(1, 2, 8);
    g.AddEdge(1, 7, 11);
    g.AddEdge(2, 3, 7);
    g.AddEdge(2, 8, 2);
    g.AddEdge(2, 5, 4);
    g.AddEdge(3, 4, 9);
    g.AddEdge(3, 5, 14);
    g.AddEdge(4, 5, 10);
    g.AddEdge(5, 6, 2);
    g.AddEdge(6, 7, 1);
    g.AddEdge(6, 8, 6);
    g.AddEdge(7, 8, 7);

    g.ReverseDeleteMST();
  }
}

// This code is contributed by Prithi_Dey

Python3

# Python3 program to find Minimum Spanning Tree
# of a graph using Reverse Delete Algorithm

# Graph class represents a directed graph
# using adjacency list representation
class Graph:
    def __init__(self, v):

        # No. of vertices
        self.v = v
        self.adj = [0] * v
        self.edges = []
        for i in range(v):
            self.adj[i] = []

    # function to add an edge to graph
    def addEdge(self, u: int, v: int, w: int):
        self.adj[u].append(v) # Add w to v’s list.
        self.adj[v].append(u) # Add w to v’s list.
        self.edges.append((w, (u, v)))

    def dfs(self, v: int, visited: list):

        # Mark the current node as visited and print it
        visited[v] = True

        # Recur for all the vertices adjacent to
        # this vertex
        for i in self.adj[v]:
            if not visited[i]:
                self.dfs(i, visited)

    # Returns true if graph is connected
    # Returns true if given graph is connected, else false
    def connected(self):
        visited = [False] * self.v

        # Find all reachable vertices from first vertex
        self.dfs(0, visited)

        # If set of reachable vertices includes all,
        # return true.
        for i in range(1, self.v):
            if not visited[i]:
                return False

        return True

    # This function assumes that edge (u, v)
    # exists in graph or not,
    def reverseDeleteMST(self):

        # Sort edges in increasing order on basis of cost
        self.edges.sort(key = lambda a: a[0])

        mst_wt = 0 # Initialize weight of MST

        print("Edges in MST")

        # Iterate through all sorted edges in
        # decreasing order of weights
        for i in range(len(self.edges) - 1, -1, -1):
            u = self.edges[i][1][0]
            v = self.edges[i][1][1]

            # Remove edge from undirected graph
            self.adj[u].remove(v)
            self.adj[v].remove(u)

            # Adding the edge back if removing it
            # causes disconnection. In this case this
            # edge becomes part of MST.
            if self.connected() == False:
                self.adj[u].append(v)
                self.adj[v].append(u)

                # This edge is part of MST
                print("( %d, %d )" % (u, v))
                mst_wt += self.edges[i][0]
        print("Total weight of MST is", mst_wt)

# Driver Code
if __name__ == "__main__":

    # create the graph given in above figure
    V = 9
    g = Graph(V)

    # making above shown graph
    g.addEdge(0, 1, 4)
    g.addEdge(0, 7, 8)
    g.addEdge(1, 2, 8)
    g.addEdge(1, 7, 11)
    g.addEdge(2, 3, 7)
    g.addEdge(2, 8, 2)
    g.addEdge(2, 5, 4)
    g.addEdge(3, 4, 9)
    g.addEdge(3, 5, 14)
    g.addEdge(4, 5, 10)
    g.addEdge(5, 6, 2)
    g.addEdge(6, 7, 1)
    g.addEdge(6, 8, 6)
    g.addEdge(7, 8, 7)

    g.reverseDeleteMST()

# This code is contributed by
# sanjeev2552

C#

// C# program to find Minimum Spanning Tree
// of a graph using Reverse Delete Algorithm

using System;
using System.Collections.Generic;

// class to represent an edge
public class Edge : IComparable<Edge> {
    public int u, v, w;
    public Edge(int u, int v, int w)
    {
        this.u = u;
        this.v = v;
        this.w = w;
    }
    public int CompareTo(Edge other)
    {
        return this.w.CompareTo(other.w);
    }
}

// Graph class represents a directed graph
// using adjacency list representation
public class Graph {
    private int V; // No. of vertices
    private List<int>[] adj;
    private List<Edge> edges;

    public Graph(int v) // Constructor
    {
        V = v;
        adj = new List<int>[ v ];
        for (int i = 0; i < v; i++)
            adj[i] = new List<int>();
        edges = new List<Edge>();
    }

    // function to Add an edge
    public void AddEdge(int u, int v, int w)
    {
        adj[u].Add(v); // Add w to v’s list.
        adj[v].Add(u); // Add w to v’s list.
        edges.Add(new Edge(u, v, w));
    }

    // function to perform dfs
    private void DFS(int v, bool[] visited)
    {
        // Mark the current node as visited and print it
        visited[v] = true;

        // Recur for all the vertices adjacent to
        // this vertex
        foreach(int i in adj[v])
        {
            if (!visited[i])
                DFS(i, visited);
        }
    }

    // Returns true if given graph is connected, else false
    private bool IsConnected()
    {
        bool[] visited = new bool[V];

        // Find all reachable vertices from first vertex
        DFS(0, visited);

        // If set of reachable vertices includes all,
        // return true.
        for (int i = 1; i < V; i++) {
            if (visited[i] == false)
                return false;
        }
        return true;
    }

    // This function assumes that edge (u, v)
    // exists in graph or not,
    public void ReverseDeleteMST()
    {
        // Sort edges in increasing order on basis of cost
        edges.Sort();

        int mst_wt = 0; // Initialize weight of MST

        Console.WriteLine("Edges in MST");

        // Iterate through all sorted edges in
        // decreasing order of weights
        for (int i = edges.Count - 1; i >= 0; i--) {
            int u = edges[i].u;
            int v = edges[i].v;

            // Remove edge from undirected graph
            adj[u].Remove(v);
            adj[v].Remove(u);

            // Adding the edge back if removing it
            // causes disconnection. In this case this
            // edge becomes part of MST.
            if (IsConnected() == false) {
                adj[u].Add(v);
                adj[v].Add(u);

                // This edge is part of MST
                Console.WriteLine("({0}, {1})", u, v);
                mst_wt += edges[i].w;
            }
        }

        Console.WriteLine("Total weight of MST is {0}",
                          mst_wt);
    }
}

class GFG {
    // Driver code
    static void Main(string[] args)
    {
        // create the graph given in above figure
        int V = 9;
        Graph g = new Graph(V);

        // making above shown graph
        g.AddEdge(0, 1, 4);
        g.AddEdge(0, 7, 8);
        g.AddEdge(1, 2, 8);
        g.AddEdge(1, 7, 11);
        g.AddEdge(2, 3, 7);
        g.AddEdge(2, 8, 2);
        g.AddEdge(2, 5, 4);
        g.AddEdge(3, 4, 9);
        g.AddEdge(3, 5, 14);
        g.AddEdge(4, 5, 10);
        g.AddEdge(5, 6, 2);
        g.AddEdge(6, 7, 1);
        g.AddEdge(6, 8, 6);
        g.AddEdge(7, 8, 7);

        g.ReverseDeleteMST();
    }
}

// This code is contributed by cavi4762

Javascript

// Javascript program to find Minimum Spanning Tree
// of a graph using Reverse Delete Algorithm

// Graph class represents a directed graph
// using adjacency list representation
class Graph {

    // Constructor
    constructor(V) {
        this.V = V;
        this.adj = [];
        this.edges = [];
        for (let i = 0; i < V; i++) {
            this.adj[i] = [];
        }
    }

    // function to add an edge to graph
    addEdge(u, v, w) {
        this.adj[u].push(v);// Add w to v’s list.
        this.adj[v].push(u);// Add w to v’s list.
        this.edges.push([w, [u, v]]);
    }

    DFS(v, visited) {
        // Mark the current node as visited and print it
        visited[v] = true;
        for (const i of this.adj[v]) {
            if (!visited[i]) {
                this.DFS(i, visited);
            }
        }
    }

    // Returns true if given graph is connected, else false
    isConnected() {
        const visited = [];
        for (let i = 0; i < this.V; i++) {
            visited[i] = false;
        }

        // Find all reachable vertices from first vertex
        this.DFS(0, visited);

        // If set of reachable vertices includes all,
        // return true.
        for (let i = 1; i < this.V; i++) {
            if (!visited[i]) {
                return false;
            }
        }
        return true;
    }

    // This function assumes that edge (u, v)
    // exists in graph or not,
    reverseDeleteMST() {

        // Sort edges in increasing order on basis of cost
        this.edges.sort((a, b) => a[0] - b[0]);

        let mstWt = 0;// Initialize weight of MST

        console.log("Edges in MST");

        // Iterate through all sorted edges in
        // decreasing order of weights
        for (let i = this.edges.length - 1; i >= 0; i--) {
            const [u, v] = this.edges[i][1];

            // Remove edge from undirected graph
            this.adj[u] = this.adj[u].filter(x => x !== v);
            this.adj[v] = this.adj[v].filter(x => x !== u);

            // Adding the edge back if removing it
            // causes disconnection. In this case this
            // edge becomes part of MST.
            if (!this.isConnected()) {
                this.adj[u].push(v);
                this.adj[v].push(u);

                // This edge is part of MST
                console.log(`(${u}, ${v})`);
                mstWt += this.edges[i][0];
            }
        }
        console.log(`Total weight of MST is ${mstWt}`);
    }
}

// Driver code
function main()
{

    // create the graph given in above figure
    var V = 9;
    var g = new Graph(V);

    // making above shown graph
    g.addEdge(0, 1, 4);
    g.addEdge(0, 7, 8);
    g.addEdge(1, 2, 8);
    g.addEdge(1, 7, 11);
    g.addEdge(2, 3, 7);
    g.addEdge(2, 8, 2);
    g.addEdge(2, 5, 4);
    g.addEdge(3, 4, 9);
    g.addEdge(3, 5, 14);
    g.addEdge(4, 5, 10);
    g.addEdge(5, 6, 2);
    g.addEdge(6, 7, 1);
    g.addEdge(6, 8, 6);
    g.addEdge(7, 8, 7);

    g.reverseDeleteMST();
}
main();

Output

Edges in MST
(3, 4) 
(0, 7) 
(2, 3) 
(2, 5) 
(0, 1) 
(5, 6) 
(2, 8) 
(6, 7) 
Total weight of MST is 37

Time complexity: O((E*(V+E)) + E log E) where E is the number of edges.

Space complexity: O(V+E) where V is the number of vertices and E is the number of edges. We are using adjacency list to store the graph, so we need space proportional to O(V+E).

Notes : 

1. The above implementation is a simple/naive implementation of Reverse Delete algorithm and can be optimized to O(E log V (log log V)³) [Source : Wiki]. But this optimized time complexity is still less than Prim and Kruskal Algorithms for MST.
2. The above implementation modifies the original graph. We can create a copy of the graph if original graph must be retained.