Check if removing a given edge disconnects a graph

Given an undirected graph and an edge, the task is to find if the given edge is a bridge in graph, i.e., removing the edge disconnects the graph. 

Following are some example graphs with bridges highlighted with red color.

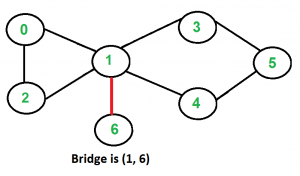
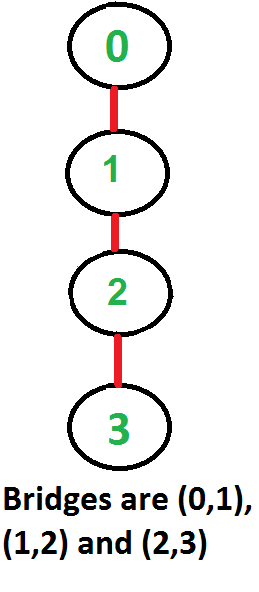
One solution is to find all bridges in given graph and then check if given edge is a bridge or not.

A simpler solution is to remove the edge, check if graph remains connect after removal or not, finally add the edge back. We can always find if an undirected is connected or not by finding all reachable vertices from any vertex. If count of reachable vertices is equal to number of vertices in graph, then the graph is connected else not. We can find all reachable vertices either using BFS or DFS. Below are complete steps.

1.  Remove the given edge 
2. Find all reachable vertices from any vertex. We have chosen first vertex in below implementation. 
3. If count of reachable nodes is V, then return false [given is not Bridge]. Else return yes. 

Implementation:

C++

// C++ program to check if removing an
// edge disconnects a graph or not.
#include<bits/stdc++.h>
using namespace std;

// Graph class represents a directed graph
// using adjacency list representation
class Graph
{
    int V;    // No. of vertices
    list<int> *adj;
    void DFS(int v, bool visited[]);
public:
    Graph(int V);   // Constructor

    // function to add an edge to graph
    void addEdge(int v, int w);

    // Returns true if graph is connected
    bool isConnected();

    bool isBridge(int u, int v);
};

Graph::Graph(int V)
{
    this->V = V;
    adj = new list<int>[V];
}

void Graph::addEdge(int u, int v)
{
    adj[u].push_back(v); // Add w to v’s list.
    adj[v].push_back(u); // Add w to v’s list.
}

void Graph::DFS(int v, bool visited[])
{
    // Mark the current node as visited and print it
    visited[v] = true;

    // Recur for all the vertices adjacent to
    // this vertex
    list<int>::iterator i;
    for (i = adj[v].begin(); i != adj[v].end(); ++i)
        if (!visited[*i])
            DFS(*i, visited);
}

// Returns true if given graph is connected, else false
bool Graph::isConnected()
{
    bool visited[V];
    memset(visited, false, sizeof(visited));

    // Find all reachable vertices from first vertex
    DFS(0, visited);

    // If set of reachable vertices includes all,
    // return true.
    for (int i=1; i<V; i++)
       if (visited[i] == false)
           return false;

    return true;
}

// This function assumes that edge (u, v)
// exists in graph or not,
bool Graph::isBridge(int u, int v)
{
    // Remove edge from undirected graph
    adj[u].remove(v);
    adj[v].remove(u);

    bool res = isConnected();

    // Adding the edge back
    addEdge(u, v);

    // Return true if graph becomes disconnected
    // after removing the edge.
    return (res == false);
}

// Driver code
int main()
{
    // Create a graph given in the above diagram
    Graph g(4);
    g.addEdge(0, 1);
    g.addEdge(1, 2);
    g.addEdge(2, 3);

    g.isBridge(1, 2)? cout << "Yes" : cout << "No";

    return 0;
}

Java

// Java program to check if removing an
// edge disconnects a graph or not.
import java.util.*;

// Graph class represents a directed graph
// using adjacency list representation
class Graph {
  int V; // No. of vertices
  ArrayList<ArrayList<Integer> > adj;
  private void DFS(int v, boolean[] visited)
  {
    // Mark the current node as visited and print it
    visited[v] = true;
    // Recur for all the vertices adjacent to
    // this vertex
    for (Integer i : adj.get(v)) {
      if (!visited[i]) {
        DFS(i, visited);
      }
    }
  }

  public Graph(int V)
  {
    this.V = V;
    adj = new ArrayList<>();
    for (int i = 0; i < V; i++) {
      adj.add(new ArrayList<>());
    }
  }

  public void addEdge(int u, int v)
  {
    adj.get(u).add(v); // Add v to u’s list.
    adj.get(v).add(u); // Add u to v’s list.
  }

  // Returns true if given graph is connected, else false
  public boolean isConnected()
  {
    boolean[] visited = new boolean[V];

    // Find all reachable vertices from first vertex
    DFS(0, visited);

    // If set of reachable vertices includes all,
    // return true.
    for (int i = 1; i < V; i++)
      if (visited[i] == false)
        return false;

    return true;
  }

  // This function assumes that edge (u, v)
  // exists in graph or not,
  public boolean isBridge(int u, int v)
  {
    // Remove edge from undirected graph
    adj.get(u).remove(Integer.valueOf(v));
    adj.get(v).remove(Integer.valueOf(u));

    boolean res = isConnected();

    // Adding the edge back
    addEdge(u, v);

    // Return true if graph becomes disconnected
    // after removing the edge.
    return (res == false);
  }

  // Driver code
  public static void main(String[] args)
  {
    Graph g = new Graph(4);
    g.addEdge(0, 1);
    g.addEdge(1, 2);
    g.addEdge(2, 3);

    if (g.isBridge(1, 2)) {
      System.out.println("Yes");
    }
    else {
      System.out.println("No");
    }
  }
}

// This code is contributed by Karandeep Singh

Python3

# Python3 program to check if removing
# an edge disconnects a graph or not.

# Graph class represents a directed graph
# using adjacency list representation
class Graph:

    def __init__(self, V):
        self.V = V
        self.adj = [[] for i in range(V)]

    def addEdge(self, u, v):
        self.adj[u].append(v) # Add w to v’s list.
        self.adj[v].append(u) # Add w to v’s list.

    def DFS(self, v, visited):

        # Mark the current node as
        # visited and print it
        visited[v] = True

        # Recur for all the vertices
        # adjacent to this vertex
        i = 0
        while i != len(self.adj[v]):
            if (not visited[self.adj[v][i]]):
                self.DFS(self.adj[v][i], visited)
            i += 1

    # Returns true if given graph is
    # connected, else false
    def isConnected(self):
        visited = [False] * self.V

        # Find all reachable vertices
        # from first vertex
        self.DFS(0, visited)

        # If set of reachable vertices
        # includes all, return true.
        for i in range(1, self.V):
            if (visited[i] == False):
                return False

        return True

    # This function assumes that edge
    # (u, v) exists in graph or not,
    def isBridge(self, u, v):

        # Remove edge from undirected graph
        indU = self.adj[v].index(u)
        indV = self.adj[u].index(v)
        del self.adj[u][indV]
        del self.adj[v][indU]

        res = self.isConnected()

        # Adding the edge back
        self.addEdge(u, v)

        # Return true if graph becomes
        # disconnected after removing
        # the edge.
        return (res == False)

# Driver code
if __name__ == '__main__':

    # Create a graph given in the
    # above diagram
    g = Graph(4)
    g.addEdge(0, 1)
    g.addEdge(1, 2)
    g.addEdge(2, 3)

    if g.isBridge(1, 2):
        print("Yes")
    else:
        print("No")

# This code is contributed by PranchalK

C#

using System;
using System.Collections.Generic;

class Graph {
  int V; // No. of vertices
  List<List<int>> adj;

  private void DFS(int v, bool[] visited) {
    // Mark the current node as visited and print it
    visited[v] = true;
    // Recur for all the vertices adjacent to
    // this vertex
    foreach (int i in adj[v]) {
      if (!visited[i]) {
        DFS(i, visited);
      }
    }
  }

  public Graph(int V) {
    this.V = V;
    adj = new List<List<int>>();
    for (int i = 0; i < V; i++) {
      adj.Add(new List<int>());
    }
  }

  public void addEdge(int u, int v) {
    adj[u].Add(v); // Add v to u’s list.
    adj[v].Add(u); // Add u to v’s list.
  }

  // Returns true if given graph is connected, else false
  public bool isConnected() {
    bool[] visited = new bool[V];

    // Find all reachable vertices from first vertex
    DFS(0, visited);

    // If set of reachable vertices includes all,
    // return true.
    for (int i = 1; i < V; i++)
      if (!visited[i])
        return false;

    return true;
  }

  // This function assumes that edge (u, v)
  // exists in graph or not,
  public bool isBridge(int u, int v) {
    // Remove edge from undirected graph
    adj[u].Remove(v);
    adj[v].Remove(u);

    bool res = isConnected();

    // Adding the edge back
    addEdge(u, v);

    // Return true if graph becomes disconnected
    // after removing the edge.
    return (res == false);
  }

  // Driver code
  public static void Main(string[] args) {
    Graph g = new Graph(4);
    g.addEdge(0, 1);
    g.addEdge(1, 2);
    g.addEdge(2, 3);

    if (g.isBridge(1, 2)) {
      Console.WriteLine("Yes");
    }
    else {
      Console.WriteLine("No");
    }
  }
}

Javascript

// Graph class represents a directed graph
// using adjacency list representation
class Graph {
    constructor(V) {
        this.V = V;
        this.adj = new Array(V);
        for (let i = 0; i < V; i++) {
            this.adj[i] = new Array();
        }
    }

    addEdge(u, v) {
        this.adj[u].push(v); // Add w to v’s list.
        this.adj[v].push(u); // Add w to v’s list.
    }

    DFS(v, visited) {
        // Mark the current node as
        // visited and print it
        visited[v] = true;

        // Recur for all the vertices
        // adjacent to this vertex
        for (let i = 0; i < this.adj[v].length; i++) {
            if (!visited[this.adj[v][i]]) {
                this.DFS(this.adj[v][i], visited);
            }
        }
    }

    // Returns true if given graph is
    // connected, else false
    isConnected() {
        let visited = new Array(this.V);
        for (let i = 0; i < this.V; i++) {
            visited[i] = false;
        }

        // Find all reachable vertices
        // from first vertex
        this.DFS(0, visited);

        // If set of reachable vertices
        // includes all, return true.
        for (let i = 1; i < this.V; i++) {
            if (visited[i] == false) {
                return false;
            }
        }
        return true;
    }

    // This function assumes that edge
    // (u, v) exists in graph or not,
    isBridge(u, v) {
        // Remove edge from undirected graph
        let indU = this.adj[v].indexOf(u);
        let indV = this.adj[u].indexOf(v);
        this.adj[u].splice(indV, 1);
        this.adj[v].splice(indU, 1);

        let res = this.isConnected();

        // Adding the edge back
        this.addEdge(u, v);

        // Return true if graph becomes
        // disconnected after removing
        // the edge.
        return (res == false);
    }
}

// Driver code

// Create a graph given in the
// above diagram
let g = new Graph(4);
g.addEdge(0, 1);
g.addEdge(1, 2);
g.addEdge(2, 3);

if (g.isBridge(1, 2)) {
    console.log("Yes");
} else {
    console.log("No");
}

Output

Yes

Time Complexity : O(V + E)

If you like GeeksforGeeks and would like to contribute, you can also write an article and mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.