Rationalization of Denomintors is a method where we change the fraction with an irrational denominator into a fraction with a rational denominator. If there is an irrational or radical in the denominator the definition of rational number ceases to exist as we can’t divide anything into irrational parts. Thus, the rationalization process comes in handy to convert these fractions with irrational denominators into fractions of integer denominators.
It is also important to understand that rationalization does not change the value of a number or function. It is a technique to re-write the fraction in a more acceptable form that is easy to understand. Readers may use a calculator to confirm that rationalization does not change the original value in the further examples used for the explanation of the method.
Rationalization Definition
As the name suggests, rationalization is a process to make a fraction rational. Rationalization is a process by which radicals in the denominator of a fraction are removed by multiplying it with an irrational number generally a conjugate or a similar radical. Rationalization makes the denominator free from radicals like square root or cube root.
Rationalizing Factor
The number or expression, by which the denominator is multiplied to convert it into rational is called the Rationalizing Factor. Some of the Rationalizing factors are tabulated below:
Denominator Form
| Rationalizing Factor
|
|---|
| √x | √x |
| a + √b | a – √b |
| a – √b | a + √b |
| √a + √b | √a – √b |
| √a – √b | √a + √b |
| p√a + q√b | p√a – q√b |
| p√a – q√b | p√a + q√b |
How to Rationalize the Denominator?
As different forms of irrational denominators need different methods to rationalize. Thus all the various methods to Rationalize the Denominator are as follows:
Rationalizing Single-Term Denominator
To rationalize a monomial square or cube root say ![Rendered by QuickLaTeX.com a\sqrt[m]{y^n}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a03f3f52daf6a7df3e55f9585bd73834_l3.png) where n < m, we multiply the numerator and denominator by the same factor say
where n < m, we multiply the numerator and denominator by the same factor say ![Rendered by QuickLaTeX.com a\sqrt[m]{y^{(m-n)}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9f3a24b0d5ea7e19d4c9289075366c15_l3.png) and we get
and we get ![Rendered by QuickLaTeX.com a\sqrt[m]{y^m}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-358da5cbcd82a539f522664c0988e91e_l3.png) which can be replaced by y, so free from the radical term. Or in other words, to rationalize a monomial square or cube root, we multiply the numerator and denominator by the same factor as the denominator. i.e., if we have
which can be replaced by y, so free from the radical term. Or in other words, to rationalize a monomial square or cube root, we multiply the numerator and denominator by the same factor as the denominator. i.e., if we have ![Rendered by QuickLaTeX.com a\sqrt[3]{5^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6998b82b38191f26159388a47d189a26_l3.png) as denominator, then we need to multiply with
as denominator, then we need to multiply with ![Rendered by QuickLaTeX.com \sqrt[3]{5^{3-2}}= \sqrt[3]{5} .](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fda0e42eea314318e62725f650898c9a_l3.png)
Example: Let us rationalize 1/√5
Solution:
1/√5 is the given expression,
So, multiple both numerator and denominator by√5
= 1/√5 × √5/√5
= √5/5
Example: Rationalize ![Rendered by QuickLaTeX.com \frac{2}{\sqrt[3]{6}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b3b9837146af08c85485627b263d2da9_l3.png) .
.
Solution:
![Rendered by QuickLaTeX.com \frac{2}{\sqrt[3]{6}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b3b9837146af08c85485627b263d2da9_l3.png) is the given expression,
is the given expression,
So, multiple both numerator and denominator by ![Rendered by QuickLaTeX.com \sqrt[3]{6^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7e5242dc3ba46c3d21fd246ada413eb3_l3.png)
![Rendered by QuickLaTeX.com = \frac{2}{\sqrt[3]{6}} \times \frac{\sqrt[3]{6^2}}{\sqrt[3]{6^2}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-327c8f10e7f79c5ad36eb42fa7b4041a_l3.png)
![Rendered by QuickLaTeX.com = \frac{2\sqrt[3]{6^2}}{\sqrt[3]{6^3}} = \frac{2\sqrt[3]{6^2}}{{6}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f45c5c4917a814df2bc612f5eff37210_l3.png)
![Rendered by QuickLaTeX.com =\frac{\sqrt[3]{6^2}}{{3}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d422bc06c4a4eda5d8284ed69ebc8226_l3.png)
Rationalizing Two Terms Denominator
If the denominator is linear and is of the form a +√b or a + i√b, then the method of rationalization of the denominator comprises multiplying both the numerator and the denominator by the algebraic conjugate a – √b or a – i√b. Due to the result of the algebraic identity (a+b)(a-b) = a2 – b2, the denominator of form a +√b or a + i√b can always be rationalized using this method.
Example: Let us rationalize 1/(1 +√5)
Solution:
Given expression is 1/(1 +√5).
So, multiple both numerator and denominator by 1 – √5
= 
= 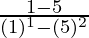 [Using identity (a+b)(a-b) = a2 – b2]
[Using identity (a+b)(a-b) = a2 – b2]
= 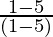
= 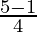
Rationalizing Three Terms Denominator
If the denominator is trinomial, like a±√b±√c (± represent all the possibilities) then it’s a little more complicated to rationalize its denominator than the method of rationalization of fraction with binomial radical as its denominator. In this case, take two terms as a single term and the third term as a second term of the rationalizing factor and then rationalize. If irrational terms are not eliminated completely after the first process of rationalization then rationalize the obtained result again with the term that remained irrational in the first rationalization process.
Let’s take 1/(1+√2-√3) for example,
Step 1: Choose any of the two given radicals to make it look like a binomial radical and multiply the fraction with its conjugate,
1/(1+√2-√3) × (1+√2+√3)/(1+√2+√3)
Note: if you choose (1+√2)-√3, then multiply the denominator and numerator with (1+√2)+√3 and if you choose (1-√3)+√2, then multiply the denominator and numerator with (1-√3)-√2.
Step 2: Simplify.
(1+√2+√3)/[(1+√2)2-(√3)2]
(1+√2+√3)/(3+2√2-3)
(1+√2+√3)/2√2
Step 3: Multiply again with √2 in numerator and denominator,
(1+√2+√3)/2√2 × √2/√2
Step 4: Simplify the result in Step 3.
(√2+2+√6)/4
Read More,
Sample Problems on Rationalization of Denominators
Problem 1: What is the interpretation of 1/√3 on a number line?
Solution:
Since the denominator has square root in the denominator, it is a bit difficult to understand. As we can not divide anything is √3 parts as it is an irrational number and it exact location on the number line depends on the number of digits taken into consideration at a time.
Let us write an equivalent expression where the denominator is a rational number using the method of rationalization.
Multiply and divide the given expression by √3.
= 1/√3 × √3/√3
= √3/3
Thus, 1/√3 =√3/3 means a point which is at one third distance from 0 to √3.
So, we can interpret the meaning of 1/√3 as a point which lies at one third distance from 0 to √3.
Problem 2: Rationalize the denominator (3 +√7)/√7
Solution:
As given expression is (3 +√7)/√7.
Multiply and divide the given expression by √7.
= (3 + √7)/√7 × (√7/√7)
= ((3 + √7)×√7 )/√7×√7
= (3√7 + 7)/7
Problem 3: Find the value of a and b, If 1/(5 + 6√3) = a√3 + b.
Solution:
Given: 1/(5 + 6√3) = a√3 + b.
Taking LHS = 1/(5 + 6√3)
Multiply and divide the given expression by 5 – 6√3 to rationalize it.
⇒ LHS ={1/(5 + 6√3)} * {(5 – 6√3)/(5 – 6√3}
⇒ LHS= {1 ×(5 – 6√3)}/{(5 + 6√3)(5 – 6√3)}
Using the identity (a + b)(a – b) = a2 – b2
⇒ LHS = (5 – 6√3)/{52 – (6√3)2}
⇒ LHS =(5 – 6√3)/ 25 – 108
⇒ LHS= (5 – 6√3)/ -83
⇒ LHS = (6√3 – 5)/83
Given that 1/(5 + 6√3) = a√3 + b
⇒ (6√3 – 5)/83 = a√3 + b
⇒ a = 6/83, b = -5/83
Problem 4: Given that √5 = 2.236. Find the value of 3/√5
Solution:
As given expression is 3/√5 .
Multiply and divide the given expression by √5
=(3/√5) × (√5 /√5)
= 3 √5 /5
= (3/5) ×√5
= 0.6 × 2.236 [ Given √5 = 2.236]
= 1.3416
Thus, 3/√5 = 1.3416
Problem 5: Rationalize the denominator of 8/(√5 – √3)
Solution:
As given Expression is 8/(√5 – √3)
Multiply and divide the given expression by √5 + √3
= (8 ×(√5 + √3))/((√5 – √3)√5 + √3))
Using the identity (a + b)(a – b) = a2 – b2
= (8√5 + 8√3)/(√52 – √32)
= 8√5 + 8√3/(5 – 3)
= 8√5 + 8√3/2
= 4√5 + 4√3
Problem 6: Simplify: (2√2 + √6 – √3)/(√2 – √3 + √6)
Solution:
As given expression if (2√2 + √6 – √3)/(√2 – √3 + √6).
To rationalize this expression, multiply the numerator and denominator by (√2 + √6 + √3).
= [(2√2 + √6 – √3)/(√2 – √6 + √3)] × [(√2 + √6+ √3)/(√2 + √6 + √3)]
= [2√2(√2 + √6 + √3) + √6(√2 + √6 + √3) – √3(√2 + √6 + √3)]/[√2(√2 + √6 + √3) – √3(√2 + √6 + √3) + √6(√2 + √6 + √3)]
Simplifying the numerator and denominator:
[(4√2 + 2√6 – √3√2 – √3√3 – √3√6)/(2 – 3 + 6)] × (√2 + √3 + √6)
Simplifying the first part of the expression:
[4√2 + 2√6 – √6 – √9 – √18]/5
[4√2 + 2√6 – √6 – 3√2 – 3√2]/5
[√2 – √6]/5
So, the simplified expression is (√2 – √6)/5.
FAQs on Rationalization of Denominators
Q1: What is the Rationalization of Denominators?
Answer:
Rationalization of denominator is the process to convert denominator of the fraction with irrational or radical expression
Q2: Why is it important to Rationalize Denominators?
Answer:
Fractions can represent parts of a whole, but when there is an irrational or radical in the denominator, the definition of the fraction no longer applies. To deal with irrational or radical denominators rationalization is used to cover these fractions into fractions with integer denominators.
Q3: What is Conjugate?
Answer:
Conjugate is the binomial formed by changing the sign of the given binomial. For example, a-√b is the conjugate of a+√b.
Q4: How do you Rationalize a Denominator With 2 Terms?
Answer:
To rationalize a denominator with 2 terms, we need to multiply both the numerator and denominator by the conjugate of the denominator and simplify.
Q5: How to Rationalize a Denominator with Square Root?
Answer:
We have to multiply the numerator and denominator with the same square root term to rationalize the denominator with square root.
Q6: How to Rationalize a Denominator with 3 Terms?
Answer:
In order to rationalize a Denominator with 3 terms take two terms as a single term and the third term as a second term of the rationalizing factor and then rationalize. If irrational terms are not eliminated completely after the first process of rationalization then rationalize the obtained result again with the term that remained irrational in the first rationalization process.
Share your thoughts in the comments
Please Login to comment...