Irrational Numbers: Definition, Examples, Symbol, Properties

Irrational numbers are real numbers that cannot be expressed as fractions. Irrational Numbers can not be expressed in the form of p/q, where p and q are integers and q ≠ 0. They are the opposite of rational numbers. They are non-recurring, non-terminating, and non-repeating decimals. Irrational numbers are real numbers but are different from rational numbers.

The symbol of irrational numbers is Q’. In this article, we will learn about irrational numbers, their properties, examples, identification, and others in detail.

Irrational Number Definition

Irrational Numbers are numbers that can not be expressed as the ratio of two integers. They are a subset of Real Numbers and can be expressed on the number line. And, the decimal expansion of an irrational number is neither terminating nor repeating.

We can define irrational numbers as real numbers that cannot be expressed as p/q where p and q are integers and q ≠ 0.

Examples of Irrational Numbers

√2, √3, π, e are some examples of irrational numbers.

• √2 = 1.41421356237309504880…
• Pi “π”= The value of π is 3.14159265358979323846264338327950… It is a famous irrational number. People have calculated its value up to quadrillion decimals but still haven’t found any pattern yet.
• Euler’s number “e” = Euler number is also very popular in mathematics. In this case, also, people tried calculating it up to a lot of decimals but still, no pattern was found. the value of e = 2.7182818284590452353602874713527 (and more …).
• Golden ratio  “ϕ” = This is an irrational number and its application is found in many fields like computer science, design, art, and architecture.

How to Identify an Irrational Number?

We know that irrational numbers are real numbers and they cannot be expressed in the form of p/q, where p and q are integers and q ≠ 0. For example, √ 5 and √ 3, etc. are irrational numbers. On the other hand, rational numbers are those that can be written as p/q, where p and q are integers and q ≠ 0.

Irrational Number Symbol

We represent the Irrational number with the symbol Q’ as it represents the group of rational numbers so Q complement (Q’) is used to represent irrational numbers. Also,

Q U Q’ = R

Where R is the set of real numbers.

How to know a Number is Irrational?

We know that rational numbers are expressed as, p/q, where p and q are integers and q ≠ 0. But we can not express the irrational number in a similar way. Irrational numbers are non-terminating and non-recurring decimal numbers. So if in a number the decimal value is never ending and never repeating then it is an irrational number.

Some examples of irrational numbers are:

• 1.112123123412345…
• -13.3221113333222221111111…, etc.

Are Irrational Numbers Real Numbers?

Irrational numbers come under real numbers, i.e. all irrational numbers are real. However irrational numbers are different from rational numbers as they can’t be written in the form of fractions. Although, irrational numbers can be expressed in the form of non-terminating and non-recurring fractions. For example,  √2, √3, and π are all irrational numbers and can’t be written as fractions.

The image below explains the relationship between Irrational numbers and Real Numbers.

Properties of Irrational Numbers

Various properties of irrational numbers are given below:

1. Sum of two rational numbers may be rational or may be irrational.
2. Sum of a rational number and an irrational number is an irrational number.
3. Product of an irrational number with a non-zero rational number is an irrational number.
4. Product of two irrational numbers may be rational or may be irrational.
5. LCM of two irrational numbers may or may not exist.
6. Set of irrational numbers is not closed under the multiplication process, but a set of rational numbers is closed.

Read More

• Properties of Real Numbers

Product of Two Irrational Numbers

Product of two rational numbers may be either rational or irrational. For example:

• π × π = π² is irrational
• √2 × √2 = 2 is rational

So Product of two Irrational Numbers can result in a Rational or Irrational Number accordingly.

Product of Irrational Number and Non-zero Rational Number

The product of any irrational number with any non-zero rational number is an irrational number. 

For example, 3 × √2 is an irrational number as it can not be represented as p/q.

Sum of Irrational Numbers

The sum of irrational numbers is sometimes rational sometimes irrational.  

• 3√2 + 4√3 is irrational.
• (3√2 + 6) + (- 3√2) = 6, is rational.

Is Pi an Irrational Number?

Yes, Pi (π) is an irrational number because it is neither terminating decimals nor repeating decimals. We will learn more about Pi (π) as:

Let’s take a circle, measure its circumference, and divide it by its diameter. It will always be a constant if measured accurately.

This constant ratio is denoted by the Greek symbol π (read as pi). That is:

Circumference/diameter = π

This decimal expansion goes on forever

Note: We often take 22/7 as the value of Pi, but it is an approximation.

Now one might think, how is Pi irrational? One can measure the circumference, One can measure the diameter, and then take their ratio. So it must be rational as we define π as:

π = Circumference/Diameter

And if we define any number as that ratio of two numbers then it is a rational number. But while defining the ratio of π, we take approximation and the value of π is never exactly equal to the ratio of Circumference and Diameter.

For more, Is pi a rational or irrational number?

Is √2  an Irrational Number?

Yes, √2 is an irrational number because it is neither terminating decimals nor repeating decimals. But we can graphically represent the value of √2 as the diagonal of the square with sides one unit as shown in the image below:

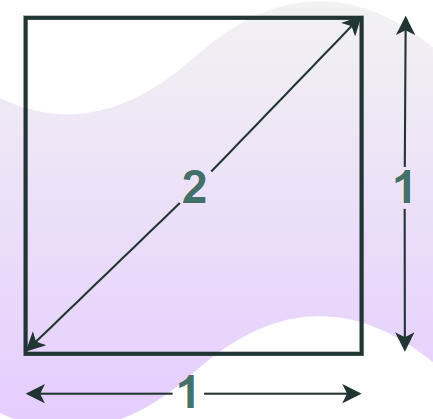
Read More about Square Root 2.

Irrational Number on Number Line

An irrational number on a number line is represented as a point that cannot be expressed as a simple fraction or ratio of integers. Unlike rational numbers, which can be depicted as points at specific positions on the number line, irrational numbers cannot be precisely pinpointed due to their non-repeating and non-terminating decimal expansions.

For example, √2 is an irrational number. When plotted on a number line, its approximate position can be determined, but its exact location cannot be identified. This is because √2 is a never-ending, non-repeating decimal. Its decimal representation goes on indefinitely without settling into a repeating pattern.

Similarly, other well-known irrational numbers such as π (pi) and e (Euler’s number) cannot be accurately represented by any finite decimal or fraction. They extend infinitely in decimal form without repeating.

List of Irrational Numbers

There are various irrational numbers that are widely used in mathematics. Some of the most commonly used irrational numbers are discussed in the table below:

Irrational Number	Symbol	Approximate Value
Pi	π	3.14159265358979…
Euler’s Number	e	2.71828182845904…
Golden Ratio	φ	1.61803398874989….

Irrational Number Theorem

The irrational number theorem is:

Theorem: If p is a prime number and p divides a², then p also divides a.

Proof:

Using the Fundamental Theorem of Arithmetic

We can say that,

a = p₁ × p₂ × p₃………..  × p_n …..(i)

where, 
p₁, p₂, p₃, ……, p_n are prime factors of a.

Squaring both sides of equation (ii)

a² = (p₁ × p₂ × p₃………..  × p_n)²

a² = (p₁)² × (p₂)² × (p₃)²…….. × (p_n)²

According to the Fundamental Theorem of Arithmetic. Every natural number has a unique prime factor.

Prime factors of a² are p₁, p₂, p₃……….., p_n. Also, the prime factors of a are, p₁, p₂, p₃……….., p_n

Thus, if a²  is divisible by p, then p also divides a.

How to Find Irrational Numbers?

An irrational Number between two prime numbers say a and b is given by √ab.

Irrational numbers between any two numbers are also found using the concept of perfect squares. We know that:

• √(1) = 1
• √(4) = 2

As the perfect squares of the number between them do not exist. So the numbers between them are irrational numbers, i.e. √(2), and √(3) are irrational numbers. Similarly the numbers

• √(4) = 2
• √(9) = 3

So the numbers between them, √(5), √(6), √(7), and √(8) are irrational numbers.

Also, the cube root of the non-perfect cube is an irrational number.

So we can say that the root of prime numbers is irrational numbers. √P  is an irrational number where P is the prime number.

This can be proved using the contradiction method is:

Statement: Square root of the prime number is an irrational number.

Proof:

Let us assume that, √u is a rational number. 

By the definition of rational numbers

√u =p/q    …….(i)

Where p and q have no common factor other than 1 and q ≠ 0

Squaring both sides of equation (1), we have

u = p²/q²

p² = uq ²    ………. (ii)

Now we can say that if u is a prime factor of p², then u is a prime factor of p.

Thus, 

p = u × c, where c is any integer.

from eq (ii)

(uc)² = uq²

q² = uc²…(iii)

From eq(iii) we can say that if u is a prime factor of q², then u is a prime factor of q.

But initially we have assumes that p and q have no common factors. But from the above proof, we say that p and q have a common factor u, which implies that our initial assumption is wrong. That is √u is not a rational number. Thus, √u is an irrational number. 

Important Points on Irrational Numbers

Non terminating, non recurring decimals are called irrational numbers.

• There are infinite rational numbers between two irrational numbers.
• There are infinite irrational numbers between two rational numbers.
• Irrational numbers can not be represented in form of p/q.

Sample Questions on Irrational Numbers

Question 1: Find Rational Numbers or Irrational Numbers among the following.

2, 3, √3, √2, 1.33333…, 1.1121231234…

Solution:

• Rational Numbers: 2, 3, 1.3333…. are rational numbers
• Irrational Numbers: √3, √2, 1.1121231234… are irrational numbers

Question 2: Find the sum of the following irrational numbers.

a) √2, √2  b) √2, √3

Solution:

a) √2 + √2 = 2√ 2 (they are added as two like variables)

b) √2 + √3 = √2 + √3 (they can’t be added as unlike variables)

Question 3: Find the product of the following rational numbers.

a) √2, √2  b) √2, √3

Solution:

a) √2 × √2 = 2

b) √2 × √3 = √6

Irrational Numbers – FAQs

What is the irrational number?

Irrational numbers are the numbers that are not defined as p/q where p and q are integers with no common factors and q does not equal to zero. They are non-terminating and non-recurring decimal numbers whose exact value can never be found.

What are examples of irrational numbers?

The examples of rational number are,

• √2 = 1.414…
• √3 = 1.732…
• Pi (π) = 3.1415…

Are integers irrational numbers?

No, Integers are not irrational numbers but are rational numbers as they can easily be represented in, p/q form. For example integers like, -1 and 2 are represented in rational number form as,

• -1 = -1/1
• 2 = 2/1

How can you identify an irrational number?

Irrational number are the numbers which are non-recurring and non-terminating decimals and we can easily identify them using this property. For example,

• 1.123123123…. is a rational number as it is a recurring decimal.
• 1.123123 is a rational number as it is a terminating decimal.
• 1.1121231234…. is an irrational number as it is non-recurring and non-terminating decimal.

Why Pi is an irrational number?

Pi(π) is an irrational number because it can not be expressed in the form of p/q and it is a non-recurring and non-terminating decimal and its value is,

π = 3.14156162…

How many irrational numbers are between 2 and 3?

There are infinite irrational number between any two real numbers and thus, there are infinite irrational number between 2 and 3.

Are rational numbers and irrational numbers same?

No, Rational Number and Irrational Number are not same.

What is difference between rational and irrational numbers?

• Rational number can be represented in the form of p/q.
• Irrational number can not be represented in form of p/q.

Is 2/3 an irrational number?

No, 2/3 is not a irrational number.

Why Pi is an irrational number?

Pi can not be represented in the form of p/q and hence it is an irrational number.

How many irrational numbers lies between root 2 and root 3?

There are infinite number between Root 2 and Root 3.

Are irrational numbers non-terminating and non-recurring?

Yes, Irrational Numbers are Non-Terminating and Non-Recurring.

Why are Irrational numbers called surds?

Surds are Non-Terminating and Non-Recurring numbers and hence they are called irrational numbers.

How to find irrational numbers between 5/7 and 9/11?

To find irrational numbers between 5/7 and 9/11, you can consider the decimal expansions of fractions. Convert both 5/7 and 9/11 into decimal form. Then, identify the digits after the decimal point that are not repeating or terminating. These non-repeating, non-terminating decimals represent irrational numbers between 5/7 and 9/11.

What are irrational numbers class 9?

In Class 9, students typically learn about irrational numbers as part of their mathematics curriculum. Irrational numbers are numbers that cannot be expressed as fractions of integers and have non-repeating, non-terminating decimal expansions. They are introduced along with rational numbers to provide a comprehensive understanding of real numbers.

Write a pair of irrational numbers whose sum is rational?

One example of a pair of irrational numbers whose sum is rational is (√2 – √2, √2 + √2). Here, (√2 – √2) equals 0, which is a rational number, and (√2 + √2) equals 2√2, which is irrational. Their sum, 0 + 2√2, is rational.