Rational Numbers Between Two Rational Numbers | Class 8 Maths
Last Updated :
23 Feb, 2021
Real numbers are categorized into rational and irrational numbers respectively. Given two integers p and q, a rational number is of the form p/q, where q > 0. A special case arises when q=1 and the rational number simply becomes an integer. Hence, all integers are rational numbers, equal to p. The number p/q reflects the ratio p:q. Some examples of rational numbers are the odd and even numbers, fractional as well as decimal numbers. All integers are also rational numbers.
Finding Rational Numbers between rational numbers
Any pair of rational numbers have an infinite number of rational numbers between them. For instance, between two whole numbers. there exist a large number of decimal numbers, which can be computed up to any number of decimal places. Given two rational numbers, f1 and f2, there exists an infinite number of rational numbers between them. The given rational numbers can be represented on the number line, and the solution must lie between them.
Same Denominator Method for finding rational numbers between rational numbers
Let us suppose the rational number f1 = p1/q1 and rational number f2 = p2/q2.
The following steps are performed to find one or more rational numbers between a pair of given rational numbers f1 and f2:
Step 1: Check the denominator values of both the fractions, that is compare the values of q1 and q2.
Step 2: If both the denominators are equal, that is q1 = q2, the numerators are then compared, that is the values of p1 and p2 are checked.
Step 3: If numerators differ by a large number, then we add any small constant integer value to the smaller numerator, keeping the denominator same. The rational numbers thus become p1/q1 and p2/q1 (since q1 = q2). Two cases may arise :
- p1 > p2 by a large amount, then we can add any numerical value to p1 such that it is less than p2, keeping the denominator same.
- p1 < p2 by a large amount, then we can add any numerical value to p2 such that it is less than p1, keeping the denominator same.
Step 4: If numerators differ by small value, then we can multiply both the rational numbers by a large constant value and follow first sub point, of adding a small constant integer to the smaller numerator. Multiplying the rational numbers by a large constant values increases the gap in the values of p1 and p2.
Sample Problems
Example 1:
Let f1 = 2/9
f2 = 38/9
Find 5 rational numbers between f1 and f2.
Solution:

Since the denominators are the same, we find fractions by adding 1 to a smaller numerator, that is, f1 numerator = 2.
3/9, 4/9, 5/9, 6/9
Example 2:
Let f1 = 2/9
f2 = 3/9
Find 7 rational numbers
Solution:

Step 1: Multiply f1 and f2 by 10
Therefore, f’1 = 20
90
f’2 = 30
90
Step 2: Now we can find the required number of rational numbers between the converted f’1 and f’2:
21/90, 22/90, 23/90, 24/90, 25/90, 26/90, 27/90
Example 3:
Let f1 = 7/11
f2 = 5/11
Find a rational number between them.
Solution:
Since the denominators are the same, we find fractions by adding 1 to a smaller numerator, that is, f2 numerator = 5.
The required fraction is = 6/11
Different Denominator Method for finding rational numbers between rational numbers
Let us suppose the rational number f1 = p1/q1 and rational number f2 = p2/q2. The following steps are performed to find one or more rational numbers between a pair of given rational numbers f1 and f2:
Step 1: Check the denominator values of both the fractions, that is compare the values of q1 and q2.
Step 2: If denominators are not equal, that is q1 ≠ q2, we first equalize denominators either by taking LCM of the two fractions or by successive multiplication of denominators of any one of the fractions to both numerator and denominator of other, such that the denominators become same.
Step 3: After, equating the denominators, we follow the Same Denominator Method to compute rational numbers between them.
Sample Problems
Example 1:
Let f1 = 3/5
f2 = 4/7, find a rational number between them.
Solution:
Since, denominators are different we take LCM of denominators, to equalize both rational number’s LCM (5, 7) = 35
Therefore f1 = f1 * 7 = 21/35
f2 = f2 * 5 = 20/35
Since, the fractions are two close, we need to increase the gap between them by multiplying them with a constant value. Multiplying both the fractions by 10 we have,
f1 = 210/350
f2 = 200/350
Now two fractions between f1 and f2 are ,
201/350 , 202/350
Example 2:
Let f1 = 1/4
f2 = 1, find a rational number between them.
Solution:
Since, denominators are different we take LCM of denominators, to equalize both rational number’s LCM (1, 4) = 4
Therefore, f1 =1/4
f2 = 4/4
Rational number between is 2/4.
Example 3:
Let f1 = 1/2
f2 = 1/8, find a rational number between them
Solution:
Since, denominators are different we take LCM of denominators, to equalize both rational number’s LCM (2, 8) = 8
Therefore f1 = f1 * 4/4 = 4/8
f2 = 1/8
One of the required rational number between 1/8 and 4/8 is 3/8.
Formula method for computing rational numbers
Irrespective of computing denominators of fractions, we can find rational numbers, between a given pair of rational numbers by finding the median of the given pair, that is, dividing them into half.
Let f1= p1/q2 and f2 = p2/q2 be the two rational numbers
Now, rational numbers between them can be computed by:
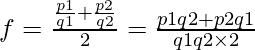
This method always finds the rational number exactly in the middle between the given pair of rational numbers.
Example 1: Let f1= 1/4
f2= 2/4
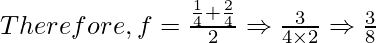
Example 2: Let f1= 1/11
f2= 3/8
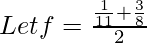
Computing LCM of fractions
⇒ (8+33)/88×2
⇒ 41/176
Share your thoughts in the comments
Please Login to comment...