Puzzle | Dividing a Square into N smaller squares
Last Updated :
06 Feb, 2023
Puzzle: Find all values of N for which one can dissect a square into N smaller squares, and outline an algorithm for doing such a dissection. Solution: The basic point to observe is a square has 4 right-angles. So, to divide it into smaller squares each of its right-angle must fall into another square, as more than one right-angle together will result in a non-square figures. Now, consider the following cases:
- When N = 2, 3, or 5: No such division is possible, as it violates the above given condition and non-shaped figures are obtained.
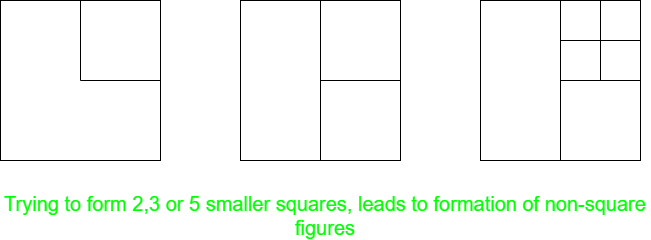
- When N = 4: This is the easiest case. Just divide the square horizontally and vertically, from the centre. The resulting figure will have 4 squares.

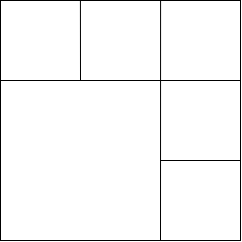
- When N is even and greater than 4: This case can be generalised by considering N = 2k and forming 2k – 1, equal squares along adjacent sides of the given square. However, the side length of each smaller square should be equal to 1/k of the length of the given square. For example: Consider the example when N = 6 as shown in the figure, here we have formed 5 squares along the top and right-side, each of side (1/3)rd of the side of the original square. Also, a square of side (2/k) is left, resulting in a total of 6 squares.
- Case N is odd and greater than 5: This case builds upon the solution for even values of N. If N is odd, we can break it as N = 2k + 1, which further can be written as N = 2(k – 1) + 3. Now, we can first form 2(k – 1) squares using the above approach, and then divide, one of the obtained squares, into four smaller squares, which will increase the overall square count by 3. For example: Consider the example when N = 9 as shown. Here, we first form 6 squares, and then divided the top-left square into 4 smaller squares, to get total 9 squares.

Share your thoughts in the comments
Please Login to comment...