Numbers in math are the most fundamental thing invented by mankind to serve its vast variety of endeavors in science and technology. From sending rockets to Mars to calculating bills for groceries, numbers are used everywhere. Nowadays, we can’t think of mathematics without Understanding numbers. There are different types of numbers like natural numbers, integers, rational numbers, irrational numbers, real numbers, complex numbers, prime numbers, composite numbers, algebraic numbers, transcendental numbers, even and odd numbers, and many, many more.
Numbers Definition
Numbers are a much-needed progression of the tally marks or counting on fingers, as numbers are the fundamental units of mathematics, without which we can’t imagine mathematics as it exists today. We use numbers to represent different quantities or values, such as weight, length, and time.
Numbers are used in a variety of tasks nowadays, including calculating, making measurements, performing data analysis, solving problems, and many more. Also, they are an essential part of the many fields of study such as science, engineering, economics, and finance.
History of Numbers
The early brain of humans was capable of grasping the concept of numbers, such that they could see how many cattle they owned or how much food would suffice for the community, but the present-day concept of numbers and counting is foreign to them. It was believed by scientists that the idea of numbers and counting originally originated in ancient societies such as Egypt, Mesopotamia, and India.
During the evolution of humans, a lot of different numerical systems were developed by humans in different parts of the world, and as the world became more connected, these systems travelled with people from one continent to another. One such numerical system, i.e., the Indian numeral system, travelled to countries in the Middle East and Europe and laid the foundation stone for the modern-day decimal system.

After reaching the Middle East, Arabic academics and scholars made noteworthy contributions to the growth of mathematics during the Middle Ages, including the usage of algebra and the decimal point. Mathematicians like John Napier and Simon Stevin introduced the ideas of decimal fractions and logarithms, respectively, in the 16th century, which helped to simplify complicated computations.
With new findings and applications in disciplines like physics, engineering, and computer science, the area of mathematics has advanced in the modern age. Today, numbers and mathematical ideas are fundamental to many key aspects of our everyday lives, from time and distance measurement to money management and data analysis.
Classification of Numbers
Based on characteristics, numbers can be classified into different types, such as:
- Natural Numbers
- Whole Numbers
- Integers
- Rational Numbers
- Irrational Numbers
- Real Numbers
- Complex Numbers
Natural Numbers
Natural Numbers, which are thought to be the first numbers to exist, are the most fundamental and obvious types of numbers. Natural numbers are defined as numbers that are used for counting. The Natural Numbers are therefore 1, 2, 3, 4, . . . and go on forever. The general representation of Natural numbers is N, and it is widely used in textbooks for the same. The image added below shows natural or counting numbers.

Whole Numbers
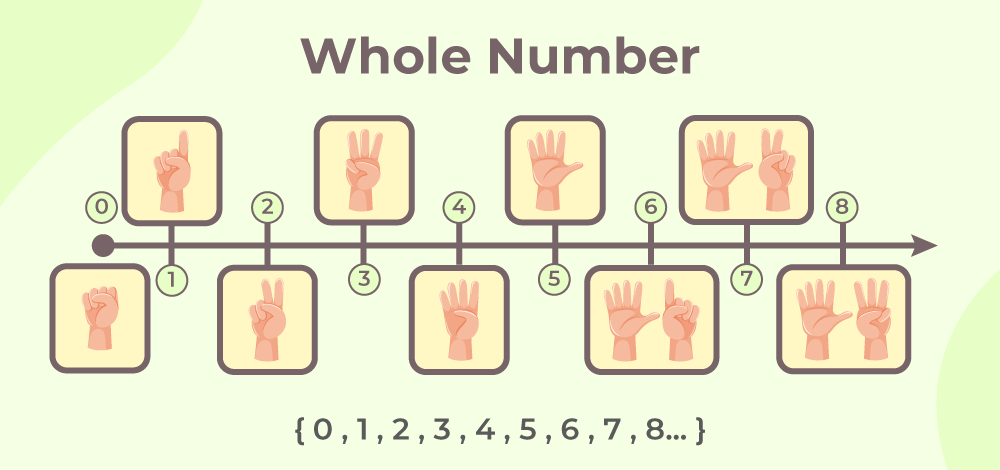
After the discovery of 0 Whole Numbers became the natural continuation of Natural Numbers. As Whole Numbers are defined as the collection of Natural Numbers including 0 i.e., 0, 1, 2, 3, 4, . . . and goes on forever. Whole Numbers are represented by the letter W. The image added below shows Whole Numbers.
Integers
When the use of negative numbers was popularized, they were very useful for many real-life use cases, such as debt-oriented calculations. Integers came into existence, as these are collections of whole numbers as well as the negative of each natural number, i.e., . . . -4, -3, -2, -1, 0, 1, 2, 3, 4, . . ., and these go forever on both sides. Integers are represented by Z.
Rational Numbers
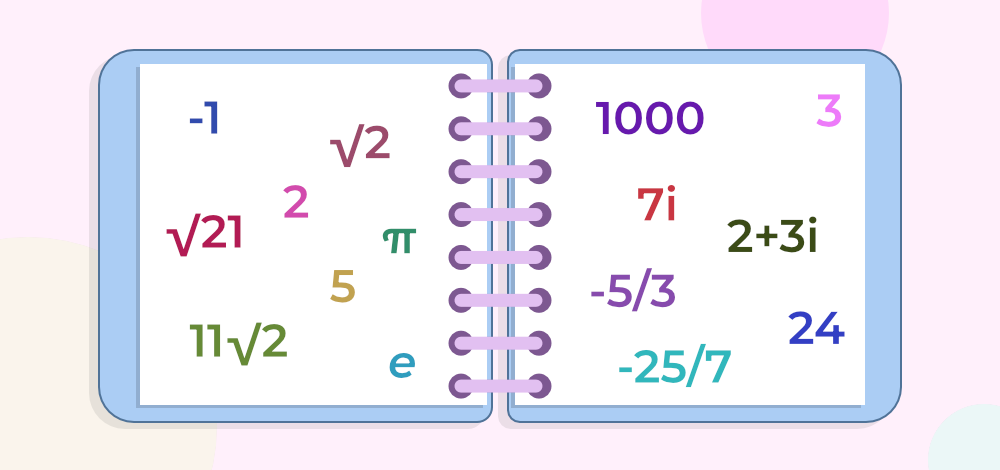
There was a problem in ancient Egypt with how to represent half or one-third of something in the records, so they came up with the solution known as fractions, and these fractions further evolved into Rational Numbers as we know them today. For a definition, Rational Numbers are those numbers that can be represented in the p/q form, where p and q are both integers and q can never be 0. For example, 1/2, 3/5, 17/41, 13/7, etc. (As we can’t list all rational numbers as a list of natural numbers or integers).
The image added below shows the rational and irrational number

Irrational Numbers
Irrational Numbers came into existence due to geometry, as Pythagoras discovered a very elegant solution for a right-angled triangle known as the Pythagoras Theorem. If there is a right-angled triangle with its base and height both being 1 unit, then using Pythagoras’ theorem, its hypotenuse comes to be √2, which back then wasn’t known as anything.
Also there was a dark story about it that goes like one of the Pythagoras’s disciple named Hippasus of Metapontum proved the existence of irrational numbers representing √2 as fraction and proofing that it is a contradiction but Pythagoras believed in the absoluteness of numbers and couldn’t accept the existence of irrational number but he also didn’t able to disproof logically that irrational numbers doesn’t exist. So, he sentenced Hippasus’ death by drowning to impede the spread of such things which were against the philosophies of Pythagoras.
Irrational numbers are defined as such numbers that can’t be represented as the ratio of two integers and are represented by P. Irrational Numbers are non-terminating and non-repeating in nature i.e. they don’t have decimal value limited to finite places and also the preparation of digits in decimal expansion is not periodic. Some examples of Irrational Numbers include √2, √3, √11, 2√2, π(pi), etc. (As we can’t list all rational numbers as a list of natural numbers or integers).
Real Numbers
The collection of rational and irrational numbers is known as Real Numbers but the name comes from the fact that they can be represented on the real number line. All the examples of rational and irrational numbers are examples of Real Numbers as well. All the numbers except imaginary numbers are included under Real Numbers. Real Numbers are represented by R.
Imaginary Numbers
For a long period of time, people thought that the number system was incomplete and needed some new sort of numbers to complete it, as there was no solution to the equation x2+a=0(where a>0) in real numbers, but we now know by the fundamental theorem of algebra that every polynomial of degree n needs to have n roots. So there must be a new sort of number needed to find the solution to the above equation.
The solution of the equation x2 + a = 0 is simply x = ±√-a, which in ancient times was not accepted as the solution because they didn’t know any such number whose square was a negative number, but eventually, some mathematicians started using such a number and saw that this made sense for a lot of other calculations as well. Some things that mathematicians saw as impossible before the use of the square root of negative numbers now seem graspable. One of the first mathematicians to use this notion was Rafael Bombelli, an Italian mathematician. Eventually, this concept of using the square root of negative numbers is becoming a useful tool for many fields of mathematics as well as physics.
A new symbol, “i(iota)” was used by Euler first for -1 so he could easily represent an imaginary number without writing √-1 repetitively, and it spread across the world and became second nature to use “i” for √-1. Numbers that give a negative value when squared are generally called Imaginary Numbers. Some examples of these numbers are √-21(which can be written as √-1×√21 or i√21), i, 2i, etc.
Complex Numbers
Complex numbers are the result of the endeavor of hundreds of mathematicians to complete the number system and are defined in the form of a+ib, where a and b are real numbers and “i” is the iota, which represents √-1. Complex numbers are represented by C and are the most useful in the different fields of modern physics, such as quantum mechanics and electromagnetic waves. Some examples of Complex Numbers are 1+i, √2-3i, 2-i√5, etc. The image added below represents the general structure of complex numbers.
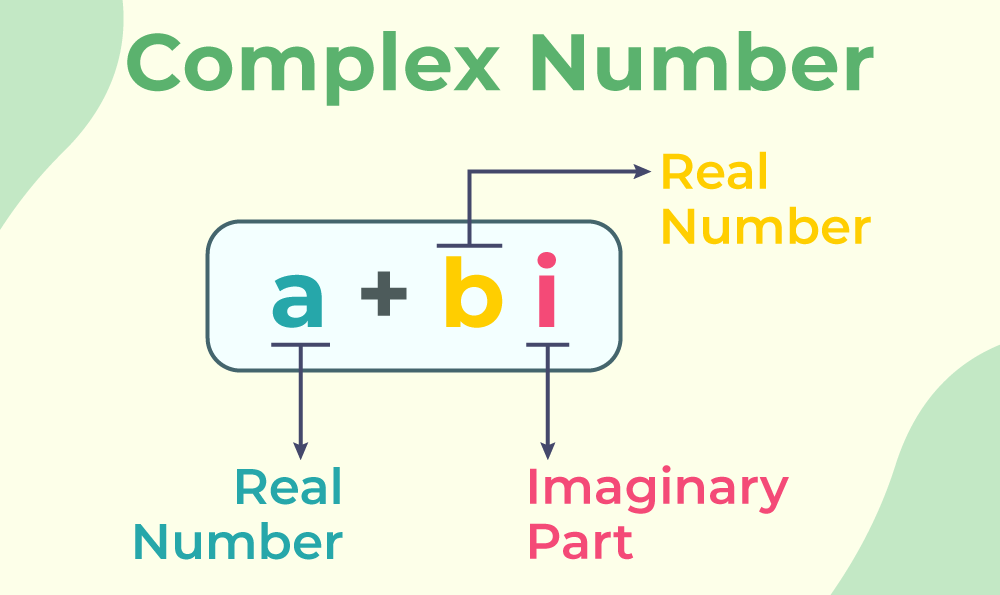
The set of numbers is discussed in the image added below which explains that all the numbers known to humans are the subset of complex numbers.
.png)
Numbers in Words
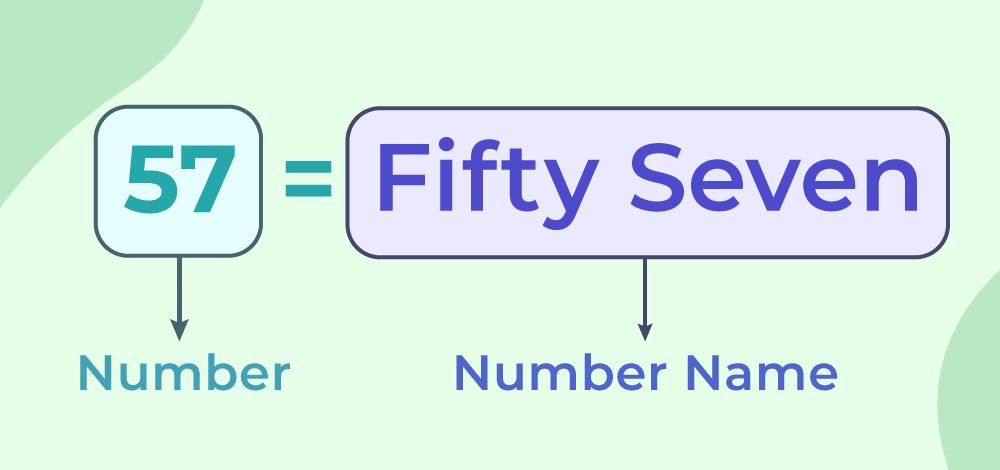
Representation of numerical values in the form of words is referred to as Numbers in Word. In this representation each digit of a number is replaced by a word, for example, the number 231 is represented as “two hundred thirty-one”.
In each number system, we have different rules for writing numbers in words. For example, in the Indian system, we separate numerals after every two digits of a number, and the names of successive higher numbers are as follows: one, ten, hundred, thousand, ten thousand, lac, ten lac, crore, ten crores, etc.
But in the international system, digits are separated according to their place value, and the names of successive higher numbers are as follows: one, ten, hundred, thousand, ten thousand, hundred thousand, million, ten million, hundred million, billion, etc.
List of first forty numbers as words as follows:
| 1 |
One |
21 |
Twenty-One |
| 2 |
Two |
22 |
Twenty-Two |
| 3 |
Three |
23 |
Twenty-Three |
| 4 |
Four |
24 |
Twenty-Four |
| 5 |
Five |
25 |
Twenty-Five |
| 6 |
Six |
26 |
Twenty-Six |
| 7 |
Seven |
27 |
Twenty-Seven |
| 8 |
Eight |
28 |
Twenty-Eight |
| 9 |
Nine |
29 |
Twenty-Nine |
| 10 |
Ten |
30 |
Thirty |
| 11 |
Eleven |
31 |
Thirty-One |
| 12 |
Twelve |
32 |
Thirty-Two |
| 13 |
Thirteen |
33 |
Thirty-Three |
| 14 |
Fourteen |
34 |
Thirty-Four |
| 15 |
Fifteen |
35 |
Thirty-Five |
| 16 |
Sixteen |
36 |
Thirty-Six |
| 17 |
Seventeen |
37 |
Thirty-Seven |
| 18 |
Eighteen |
38 |
Thirty-Eight |
| 19 |
Nineteen |
39 |
Thirty-Nine |
| 20 |
Twenty |
40 |
Forty |
The image added below tells us how we write a number in words
Operations on Numbers
Operations on Numbers are the most fundaments building block of mathematics and are used to manipulate numerical values. These operations are as follows:
Division
In Division, we can divide a number into equal parts. For example, 12 ÷ 3 = 4 means 12 can be shared into 3 equal parts, each part is 4. The image added below shows the division between 21 ÷ 7 =3.

Multiplication
Multiplication is used when we need to add a number a certain number of times, so instead of repeatedly adding it, we just multiply it by the number of times it needs to be added. For example, 3 x 4 = 12 means 3 + 3 + 3 + 3 = 12. The image added below shows the multiplication between 21 × 3 = 63.
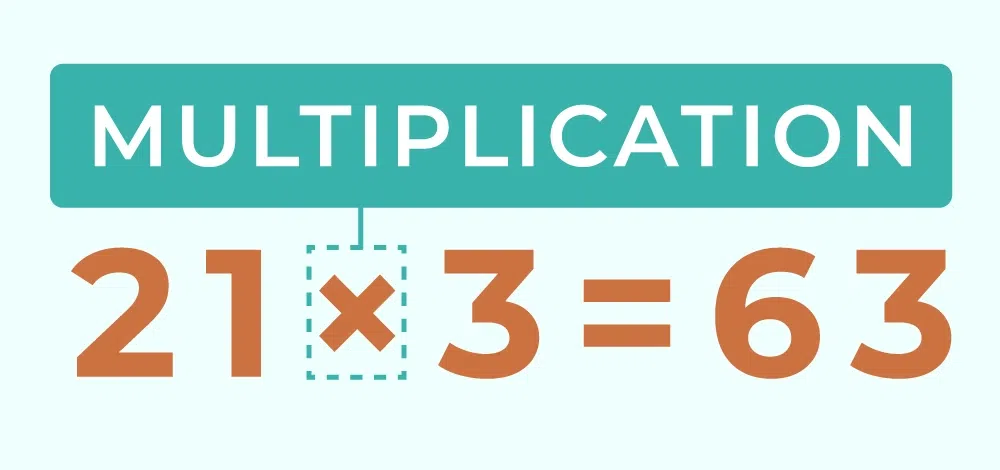
Addition
The addition is the most basic operation which combines two or more numbers to get a sum. For example, 2 + 3 = 5, 3+1/2=7/2, 2.14 + 3.73 = 5.87, etc. The image added below shows the addition between 21 + 3 = 24.
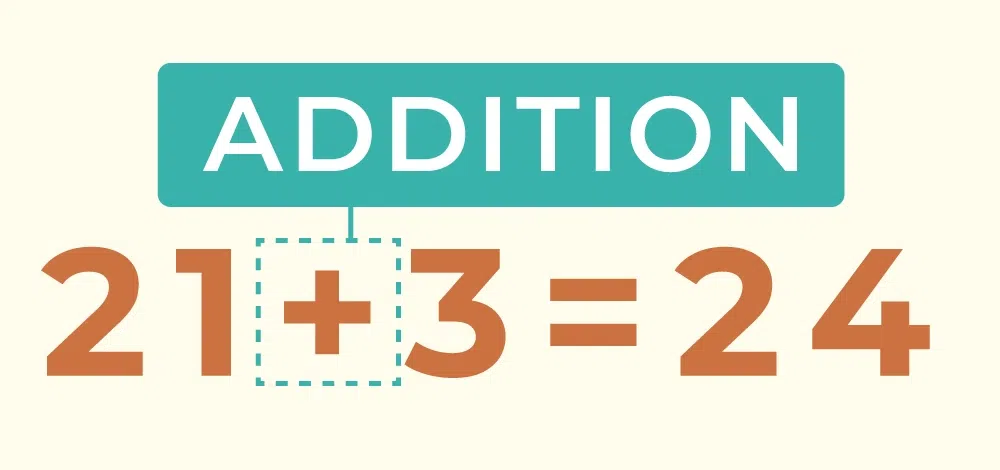
Subtraction
Subtraction is used for finding the difference between two numbers. For example, 6 – 4 = 2, 3-1.5 = 1.5, 3/2-1/3 = 7/3, etc. The image added below shows the addition between 21 – 3 = 18.

Types of Numbers
Apart from the above types, there are some types of numbers that are based on the properties of the numbers. Some of these numbers are,
- Cardinal and Ordinal Numbers
- Even and Odd Numbers
- Prime and Composite Numbers
- Co Prime Numbers
- Perfect Numbers
- Algebraic and Transcendental Numbers
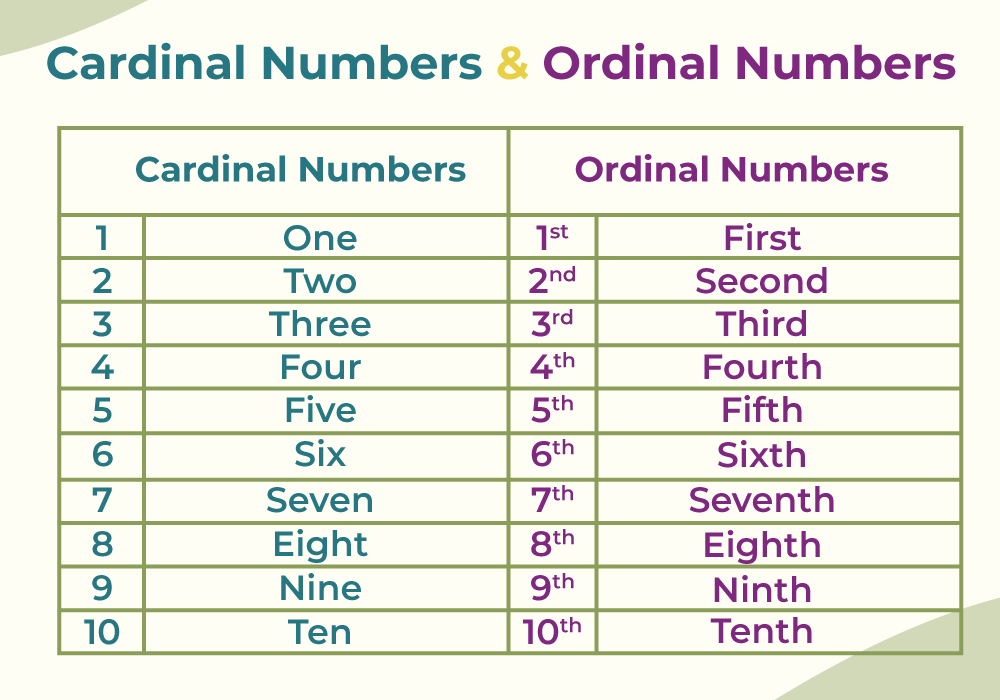
Cardinal and Ordinal Numbers
Cardinal Numbers are the same as natural numbers as they were defined as sequentially going numbers that start from 1 and go on forever i.e. 1, 2, 3, 4, . . . and so on.
An ordinal Number is a number that shows the exact position or the order of the object in the sequence. For example first, second, third, and so on. The Cardinal and Ordinal Numbers from 1 to 10 are discussed in the image below,
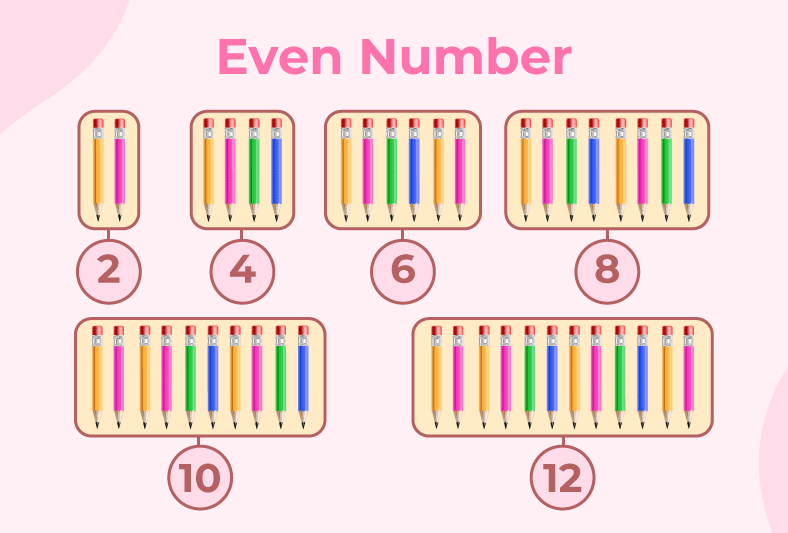
Even and Odd Numbers
For all the integers, it is true that either they are divisible by 2 or they are not divisible by 2. Those numbers that are divisible by 2 are called even numbers, and those that are not divisible by 2 are called odd numbers. The image added below shows the Even Numbers.
The image added below shows the Odd Numbers.

Examples of Even Numbers are 0, 2, 4, 6, . . . and so on, as well as negative numbers, i.e., -2, -4, -6, . . ., and so on. Examples of Odd Numbers are 1, 3, 5, 7, . . ., and so on, as well as negative numbers, i.e., -1, -3, -5, -7, . . . and so on.
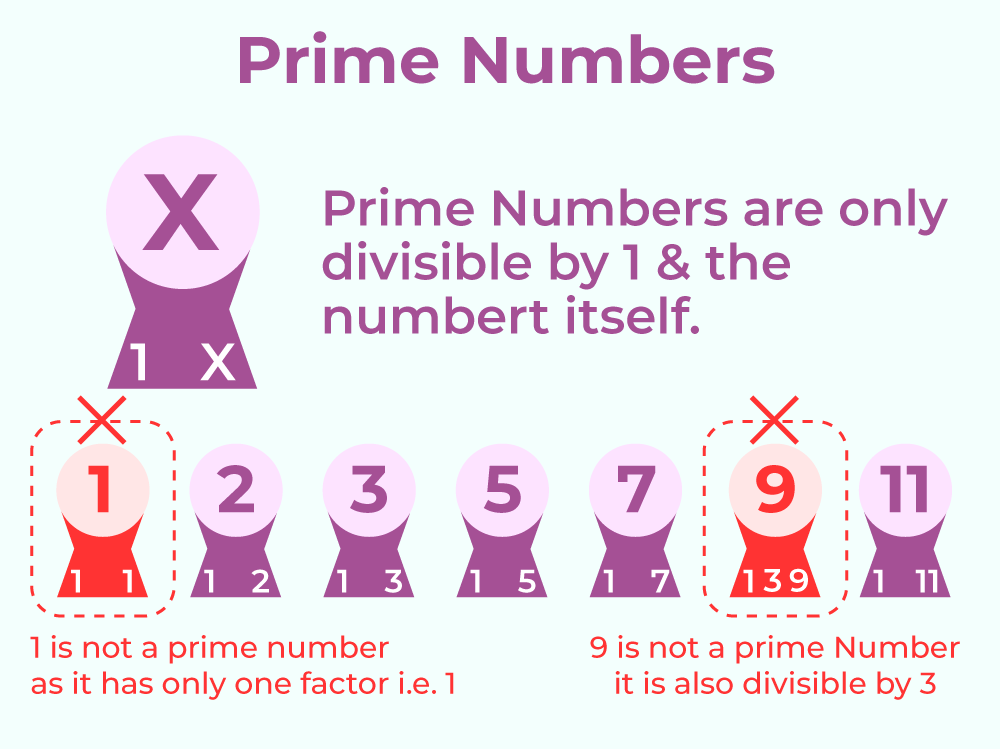
Prime and Composite Numbers
Natural Numbers that are divisible by either 1 or themselves are known as Prime Numbers and if there are any other divisors of a number other than 1 and itself, then it is called a composite number. The smallest prime number is 2, and some other examples of Prime Numbers are 3, 5, 7, 11, etc. Also, some examples of composite numbers are 4, 6, 8, 9, and many, many more.
Note: 1 is neither Prime nor Composite Number.
The following image shows the prime numbers.
Coprime Numbers
In mathematics, two numbers a and b (which do not need to be prime) are called Coprime Numbers, relatively prime or mutually prime, if and only if they only have 1 as their common factor. For example,4=22 and 9=32 both only have 1 as their common factor, or we can also say that the HCF of 4 and 9 is 1. So, 4 and 9 are Coprime Numbers.
Some more examples of coprime pairs are 12 and 25, 8 and 15, 24 and 35, etc. The following image shows how 21 and 22 are co-prime numbers.

Perfect Numbers
Perfect numbers are those natural numbers whose sum of divisors excluding themselves is equal to the number itself, i.e., if we calculate the sum of divisors of a number excluding itself and it comes out to be the same as the original number, then that number is called a Perfect Numbers. For example, consider 6, whose divisors are 1, 2, and 3, and whose sum is 6. Thus, 6 is the Perfect Number and its image is added below,
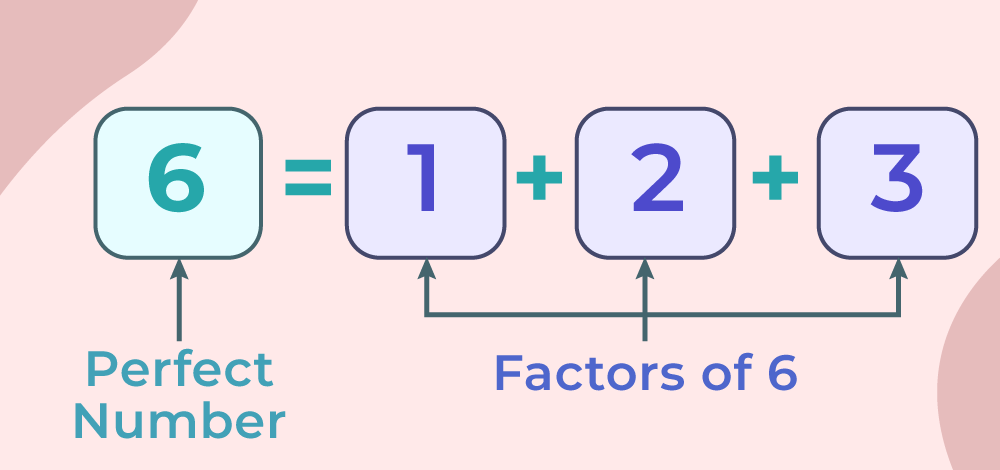
Some other examples are 28, 496, 8128, etc.
Algebraic and Transcendental Numbers
All the numbers mentioned above are examples of Algebraic Numbers that are defined as the solutions of some algebraic equations, i.e., Algebraic Numbers are those numbers that are the solutions of some algebraic equations. For example, the solution of x2+1=0 is ±√-1, which is an algebraic number. Some other examples are all the real numbers as well as complex numbers.
On the other hand, all such numbers which can’t be found as a solution to some algebraic equation are called Transcendental Numbers. Some of the most famous examples of Transcendental Numbers are π(pi) and e(Euler’s number)
Check: Find the Missing Number
Prime Factorization
Expressing any composite number as the product of prime numbers is called prime factorization. The prime factorization of a number “x” can be found easily by dividing x by the smallest possible prime number and then repeating the process until the quotient is either a prime number or 1. For example, prime factorization of 12 = 2×2×3 or 22×3. Some more examples are 15 = 5×3, 33=3×11, 42=2×3×7, etc. The prime factor of 18 is discussed in the image below.
.png)
HCF
HCF (Highest Common Factor) is the largest possible number that can divide two or more numbers without leaving any remainder. HCF is also called Greatest Common Divisor. For example, 6 is the HCF of 12 and 18, 12 is the HCF of 12 and 24, 7 is the HCF of 14 and 21, etc. The image discussed below shows the HCF of 12 and 18.
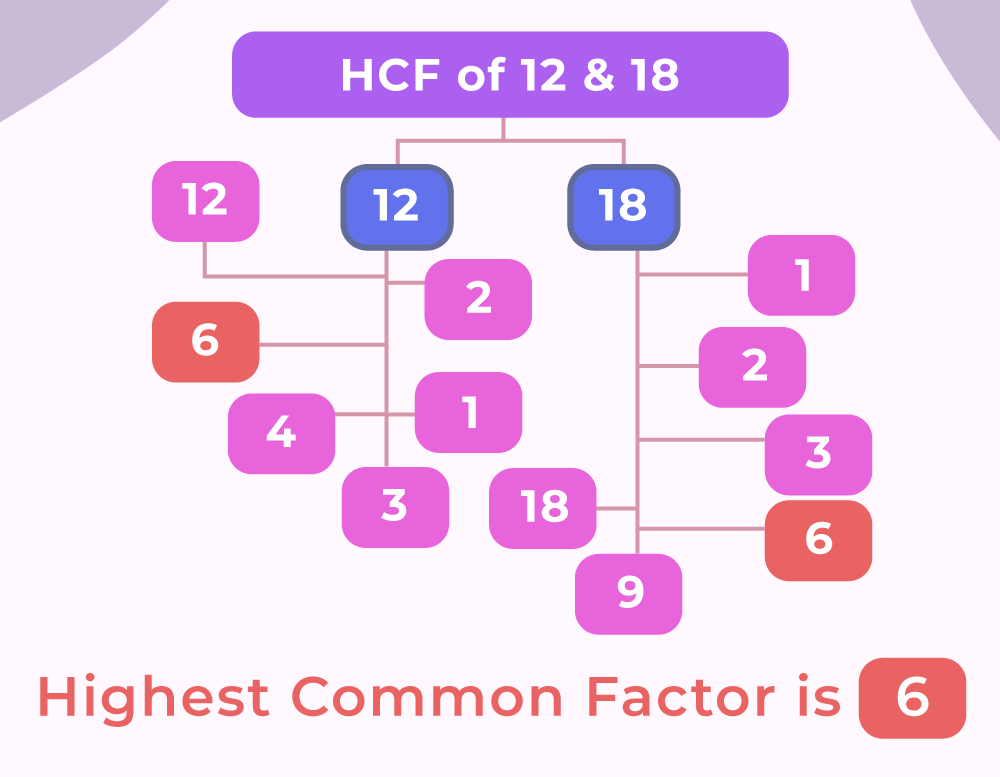
LCM
LCM (Lowest Common Multiple) of any two or more numbers is the smallest possible number when divisible by all the given numbers, yields a remainder of 0. In other words, the LCM of any two or more numbers is the smallest common multiple of all numbers. For example, the LCM of 12 and 14 is 84, LCM(21, 24) = 168, LCM(42, 122) = 2562, etc. The image discussed below shows the LCM of 4 and 6.
.webp)
Number System
The Number System is the set of guidelines that gives meaning to expressions written in that number system. For example, if we want to express that we have ten dogs, in the decimal number system we would write “10 dogs,” in the binary system “1010 dogs,” in the octal system “12 dogs,” and in the hexadecimal system “A dogs.” All these statements represent ten dogs but in different number systems.
Any Number System needs two things to express all the numbers we want it to represent. First are the symbols (generally all number systems that need less than or equal to 10 symbols use modern-day decimal numerals), and the second is the base (which is the number of required symbols). For example, in the decimal number system, there are ten symbols, so its base is 10.
Decimal Number System
The Decimal Number System is the most used number system out of all. There are 10 digits in this number system, which are 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. The decimal numbers are represented as,
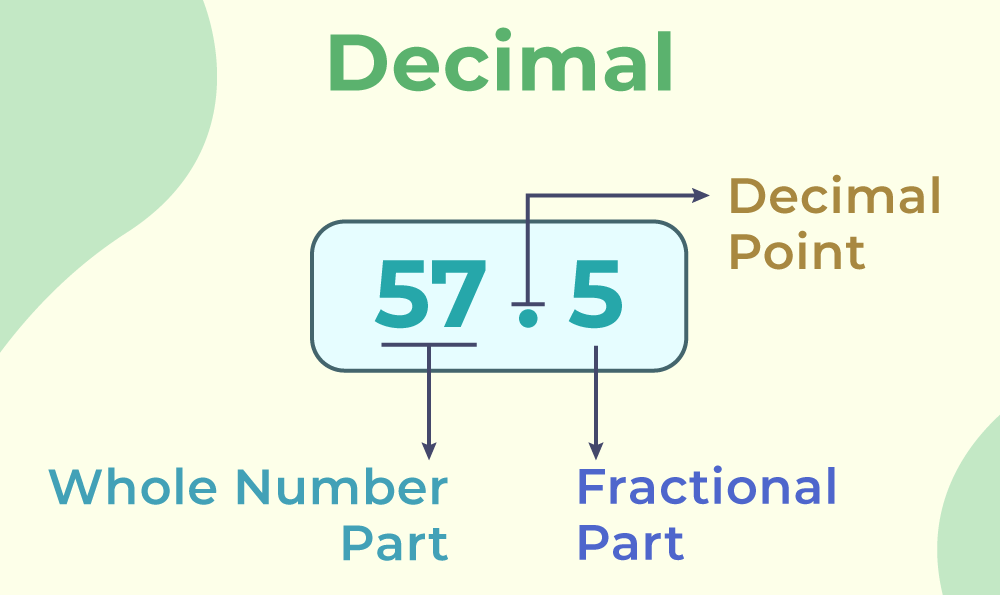
Binary Number System
In the Binary Number System, there are only two digits, and using those, we express all the numbers. The most common numerals for the Binary System are 0 and 1, but we can use any pair of symbols to represent the same as long as the symbols are well-defined. For example, 10010001, 11011001, and 1010 are some examples of binary numbers which in decimals represent 145, 217, and 10 respectively.
For a Better understanding of the conversion of binary to decimal read this article. In the binary system, we use two bits 0 and 1 as shown in the image below,

Octal Number System
In the Octal Number System, there are only 8 digits or symbols which are generally represented with modern-day decimal symbols by only up to 7 i.e., 0, 1, 2, 3, 4, 5, 6, 7. Using these 8 symbols we can write and express all the numbers. For example, 231, 41, and 653 are some examples of octal numbers which in decimals represent 153, 33, and 427 respectively. The digits used in the Octal Number system are shown in the image below,

Hexadecimal Number System
In the Hexadecimal Number System, there are 16 numerals: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, and F. It is widely used in programming-related tasks as its base is 16 (which is a multiple of 2), which is the foundation of computing as every bit can only have two values: on or off. Some examples of the Hexadecimal Number System are A1, 2A, and F3, which in the decimal number system represent 161, 42, and 243, respectively.
Check: Lucky Numbers
Properties of Numbers
There are some properties that different types of numbers have with different defined operations such as addition or multiplication, and those properties are as follows,
- Commutative Property
- Associative Property
- Distributive Property
- Identity Property
- Inverse Property
- Reflexive Property
- Symmetric Property
- Transitive Property
Commutative Property
For any two numbers a and b, for any operation ×, if a×b=b×a, then × is commutative for those sets of numbers. For example, addition and multiplication of all complex numbers hold the commutative property but with subtraction and division, they don’t hold commutative property.
Associative Property
For any three numbers a, b, and c, and any operation ×, if a×(b×c)=(a×b)×c, then × operations hold the associative property for those sets of numbers. For example, For example, addition and multiplication of all complex numbers hold the associative property but with subtraction and division, they don’t hold associative property.
Distributive Property
Distributive Property is defined for a pair of operations, say o and ×. For some numbers a, b, and c if ao(b×c) = aob×aoc then o distributes over ×, and if a×(boc) = a×boa×c then × distributes over o. For example, multiplication distributes over addition but addition doesn’t distribute over multiplication.
Identity Property
Identity is the uniquely defined number with respect to an operation such that operating identity to any number results in the number itself i.e., for operation ×, a × e = a (where e is the identity w.r.t operation ×). For example, 0 is the identity for the addition operation as a + 0 = a and 1 is the identity of multiplication as a × 1 = a.
Inverse Property
The Inverse is the uniquely defined number for each number with respect to some operation, such that when operating any number with its inverse, the output is an identity for that operation. In other words, for some number a and operation ×, where e is the identity, if a×b=e then b is called the inverse of a with respect to operation ×. For example, -1 is the inverse of 1 under addition as 1+(-1) = 0 (0 is the identity of addition), and 1/2 is the inverse of 2 under multiplication as 1/2×2=1(1 is the identity of multiplication).
Check: Number Theory for DSA & Competitive Programming
Solved Examples on Numbers
Example 1: Find the LCM of 12 and 18.
Answer:
Multiples of 12 are 12, 24, 36, 48, 60, 72, …
Multiples of 18 are 18, 36, 54, 72, …
We can see that 36 is the smallest number that is divisible by both 12 and 18.
Hence, the LCM of 12 and 18 is 36.
Example 2: Find the HCF of 24 and 36.
Answer:
Factors of 24 are: 1, 2, 3, 4, 6, 8, 12, 24
Factors of 36 are: 1, 2, 3, 4, 6, 9, 12, 18, 36
We can see that 12 is the largest number that is common to both 24 and 36.
Hence, the HCF of 24 and 36 is 12.
Example 3: Find the prime factorization of 72.
Answer:
We can start by dividing 72 by its smallest prime factor, which is 2.
72 ÷ 2 = 36
Now, we can divide 36 by its smallest prime factor, which is 2.
36 ÷ 2 = 18
Again, we can divide 18 by its smallest prime factor, which is 2.
18 ÷ 2 = 9
Again, we can divide 9 by its smallest prime factor, which is 3.
9÷ 3 = 3
3 is a prime number, so we can stop here.
Therefore, the prime factorization of 72 is 2 × 2 × 2 × 3 × 3.
Example 4: Write 2341, 3247,981472 in words (in Indian System).
Answer:
2,341: “Two Thousand Three Hundred Forty-One”
3,247: “Three Thousand Two Hundred Forty-Seven”
9,81,472: “Nine Lac Eighty-One Thousand Four Hundred Seventy Two”
Check: Number System in Maths
Numbers in Math – FAQs
What Are Numbers in Math?
Numbers in math are fundamental concepts used to count, measure, and label. They are arithmetic values that represent quantities and are essential for calculations. Numbers are used in various measurements like temperature, weight, length, and more.
How many prime numbers are between 1 and 100?
There are 25 prime numbers between 1 and 100, and those are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
How many odd numbers are there between 32 and 53?
As we know, that number is odd if and only it is not divisible by 2 or in other words every other number is odd number if we take numbers one after another. As 32 is divisible by 2 next number is not divisible by 2 i.e. 33.
Thus list of all odd numbers between 32 and 53 are 33, 35, 37, 39, 41, 43, 45, 47, 49, 51.
So, there are 10 odd numbers in between 32 and 53.
What are natural numbers?
The numbers which are used for the countings are called the natural numbers e.g of natural numbers are 1, 2, 3, …. We represent natural number by N.
Is ‘0’ a natural number?
No ‘0’ is not a natural number. It comes under the category of whole number.
How Many Types of Numbers Are There?
There are several types of numbers, including:
- Natural Numbers: Counting numbers starting from 1.
- Whole Numbers: Natural numbers including zero.
- Integers: Whole numbers and their negatives.
- Rational Numbers: Numbers that can be expressed as a fraction.
- Irrational Numbers: Numbers that cannot be expressed as a simple fraction.
- Real Numbers: All rational and irrational numbers.
Why Are Numbers Important?
Numbers are crucial for understanding and interacting with the world around us. They allow us to quantify objects, perform calculations, solve problems, and make precise measurements in science, technology, engineering, and mathematics (STEM).
How Are Numbers Used in Everyday Life?
In everyday life, numbers are used for:
- Budgeting and Financial Planning: Managing expenses and savings.
- Time Management: Keeping track of time and scheduling.
- Cooking and Baking: Measuring ingredients accurately.
- Shopping: Comparing prices and calculating discounts.
Can Numbers Be Negative?
Yes, numbers can be negative. Negative numbers are used to represent values less than zero, commonly found in temperatures below freezing, elevations below sea level, or financial debts.
Share your thoughts in the comments
Please Login to comment...