NCERT Solutions for Class 9 Maths Chapter 1 Number Systems

NCERT Solutions for Class 9 Maths Chapter 1 – Number Systems is developed by GFG Experts to assist students in solving problems related to this chapter with ease and without frustration. You can find all the problems of this chapter in NCERT Solutions for Class 9 Maths.

Class 9 Maths Chapter 1 – Number Systems covers the different types of numbers and their properties. After giving a brief overview of number systems, the chapter discusses natural numbers, whole numbers, integers, rational and irrational numbers, as well as real numbers. The chapter also covers real number operations, real number attributes, real number applications, and real number representation on the number line.

Class 9 Maths NCERT Solutions Chapter 1 Exercises:
NCERT Maths Solutions Class 9 Exercise 1.1 – 4 Questions & Solutions (4 short Answers)
NCERT Maths Solutions Class 9 Exercise 1.2 – 4 Questions & Solutions (4 short Answers)
NCERT Maths Solutions Class 9 Exercise 1.3 – 9 Questions & Solutions (8 short Answers, 1 long Answer)
NCERT Maths Solutions Class 9 Exercise 1.4 – 2 Questions & Solutions (2 long Answers)
NCERT Maths Solutions Class 9 Exercise 1.5 – 5 Questions & Solutions (4 short Answers, 1 long Answer)
NCERT Maths Solutions Class 9 Exercise 1.6 – 3 Questions & Solutions (3 short Answers)

Number Systems: Exercise 1.1

Question 1: Is zero a rational number? Can you write it in the form p/q, where p and q are integers and q ≠ 0?

Solution:

A number is a rational number if it can be written in the form of p/q, where p and q are integers and q ≠ 0

• Therefore, we can write 0 in the form of 0/1, 0/2, 0/3, 0/4.
• As well as, q can be a negative integer also, 0/-1, 0/-2, 0/-3, 0/-4.
  So we can see 0 can be written in p/q, form hence 0 is a rational number.

Question 2: Find six rational numbers between 3 and 4.

Solution: 

We can find infinite rational numbers between 3 and 4.
Now we have to find 6 rational numbers between 3 and 4 we will multiply and divide both the numbers 3 and 4 by (6 + 1) 7.

• 3 = 3 × 7/7 = 21/7
• 4 = 4 × 7/7 = 28/7

Hence the 6 rational numbers are 23/7, 24/7, 25/7, 26/7, 27/7, and 28/7.

Question 3: Find five rational numbers between 3/5 and 4/5.

Solution: 

We need to find 5 rational numbers between 3/5 and 4/5.
Multiply both numerator and denominator by (5 + 1) 6.

•  3/5 = 3/5 × 6/6 = 18/30 
•  4/5 = 4/5 × 6/6 = 24/30 

Hence, the 5 rational number between 3/5 and 4/5 are 19/30, 20/30, 21/30, 22/30 and 23/30.

Question 4: State whether the following statements are true or false. Give reasons for your answers.

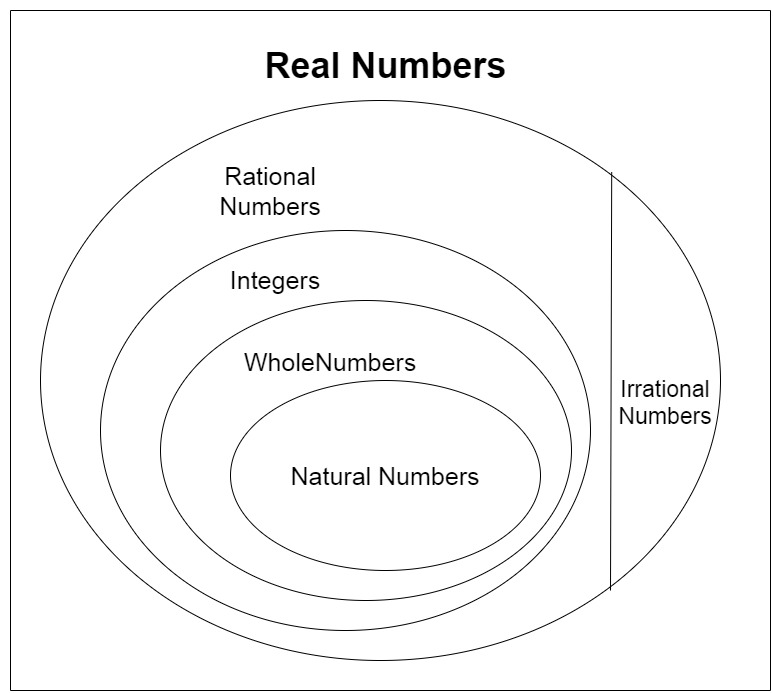
(i) Every natural number is a whole number.

(ii) Every integer is a whole number.

(iii) Every rational number is a whole number.

Solution:

(i) Every natural number is a whole number.

True

Explanation: The natural numbers starts from 1, 2, 3, 4 …..
The whole number starts from 0, 1, 2, 3 , 4 …..
Here it is clearly seen that whole number contains all the natural numbers and 0 also
Therefore, every natural number is a whole number but not every whole number is not a natural number as 0 is a whole number but not a natural number.

(ii) Every integer is a whole number.

False

Explanation: Integers are the numbers that have both positive and negative numbers including 0,

Example: …..-4, -3, -2, -1, 0, 1, 2, 3, 4 ……
Whereas whole numbers begin from 0 to infinite
Example: 0, 1, 2, 3, 4…..
Here we can see every whole number is an integer but not all the integers are the whole number.

(iii) Every rational number is a whole number.

False

Explanation: Rational numbers are the numbers that can be written in the form of p/q where q ≠ 0.

Example: 0, 2/5, 4/17, 7/15 …..

Whole numbers are that starts from 0 to infinity
As we know whole numbers can be written in the form of 0/1, 1/1, 2/1, …

Thus, every whole number is a rational number but every rational number is not a whole number.

Number Systems: Exercise 1.2

Question 1: State whether the following statements are true or false. Justify your answers.

(i) Every irrational number is a real number.

(ii) Every point on the number line is of the form √m , where m is a natural number.

(iii) Every real number is an irrational number.

Solution: 

(i) Every irrational number is a real number.

True
Irrational numbers are the number that cannot be written in the form of p/q , p and q are the integers and q ≠ 0.
Some examples of irrational numbers are π, √3, e, √2, 011011011…..

Real numbers include both rational numbers and irrational numbers.
Thus, every irrational number is a real number.

(ii) Every point on the number line is of the form √m, where m is a natural number.

False
We can represent both negative and positive numbers on a number line.
Positive numbers can be written as √16=4 that is a natural number, But √3=1.73205080757 is not a natural number.
But negative numbers cannot be expressed as the square root of any natural number, as if we take square root of an negative number it will become complex number that will not be a natural number (√5=5i is a complex number).

(iii) Every real number is an irrational number.

False
Every irrational number is a real number but every real number is not an irrational number as real numbers include both rational and irrational number.

Question 2: Are the square roots of all positive integers irrational? If not, give an example of the square root of a number that is a rational number.

Solution: 

No, the square roots of all positive integers in not irrational. For example √9 = 3, √25 = 5, hence square roots of all positive integers is not irrational.

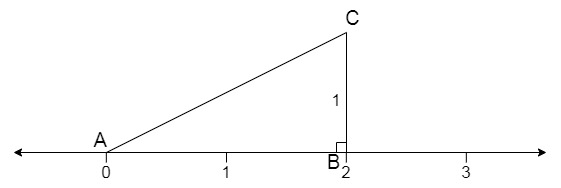
Question 3: Show how √5 can be represented on the number line.

Solution: 

To represent √5 on the number line follow the following steps:
Step 1: Draw a number line.

Step 2: Let line AB of 2 units on the number line.

Step 3: Now draw a perpendicular of unit 1 on point B and mark the other end as point C.

Step 4: Join AC, you will have triangle ABC which is a right-angle triangle. as shown below:

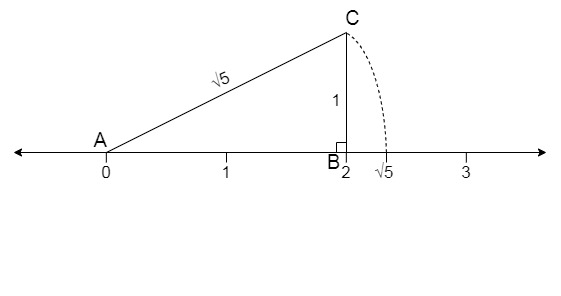
Step 5: Apply Pythagoras Theorem on triangle ABC,

⇒ AB² + BC² = AC²
⇒ AC² = 2² + 1²
⇒ AC² = 5
⇒ AC = √5
Therefore, line AC is of √5 unit length.

Step 6: Now take line AC as the radius and an arc and intersect it to number line, the point where the arc will intersect the number line is of lengths √5 from point 0 to the intersection as point A is the centre of the radius.

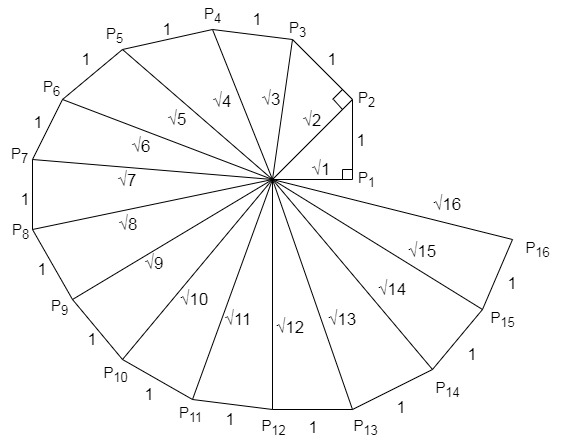
Question 4: Classroom activity (Constructing the ‘square root spiral’): Take a large sheet of paper and construct the ‘square root spiral’ in the following fashion. Start with a point O and draw a line segment OP₁ of unit length. Draw a line segment P₁ P₂ perpendicular to OP₁ of unit length (see Fig. 1.9). Now draw a line segment P₂ P₃ perpendicular to OP₂. Then draw a line segment P₃ P₄ perpendicular to OP₃. Continuing in this manner, you can get the line segment P_n-1P_n by drawing a line segment of unit length perpendicular to OP_n-1. In this manner, you will have created the points P₂, P₃, …., P_n, …., and joined them to create a beautiful spiral depicting √2, √3, √4, …

Solution: 

Step 1: First lets mark a point O on the larger sheet of paper, this point will be the centre of the square root spiral.

Step 2: Draw point P₁ from point O of 1 unit. OP₁=1 unit.

Step 3: Similarly as in the above problem from P₁ draw a perpendicular of 1 unit, P₁P₂ = 1 unit.

Step 4: Now join OP₂ = √2

Step 5: From point P₂ draw a perpendicular of 1 unit. P₂P₃ = 1 unit.

Step 6: Now join OP₃ = √3

Step 7: Now repeat the step to make √4, √5, √6, …….

Number Systems: Exercise 1.3

Question 1. Write the following in decimal form and say what kind of decimal expansion each has :

(i) 36/100 

Solution:

In the given question, we get

Here, the remainder becomes zero.

Hence, decimal expansion becomes terminating.

36/100 = 0.36

(ii) 1/11 

Solution:

In the given question, we get

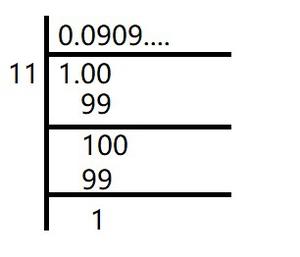
Here, the remainder never becomes zero and remainders repeat after a certain stage.

Hence, decimal expansion is non-terminating recurring

1/11 =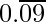 

(iii)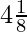 

Solution:

Here,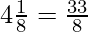 

In the given question, we get

Here, the remainder becomes zero.

Hence, decimal expansion becomes terminating.

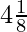 = 4.125

(iv) 3/13 

Solution:

In the given question, we get

Here, the remainder never becomes zero and remainders repeat after a certain stage.

Hence, decimal expansion is non-terminating recurring

3/13 = 

(v) 2/11 

Solution:

In the given question, we get

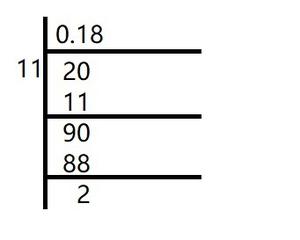
Here, the remainder never becomes zero and remainders repeat after a certain stage.

Hence, decimal expansion is non-terminating recurring

2/11 =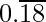 

(vi) 329/400 

Solution:

In the given question, we get

Here, the remainder becomes zero.

Hence, decimal expansion becomes terminating.

329/400 = 0.8225

Question 2. You know that 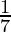= 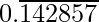Can you predict what the decimal expansions of 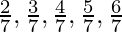are, without actually doing the long division? If so, how?

[Hint: Study the remainders while finding the value of 1/7 carefully.]

Solution:

As it is given,

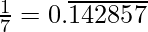
So, 

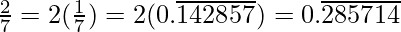
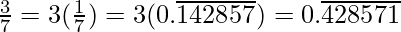
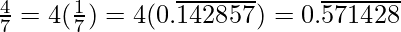
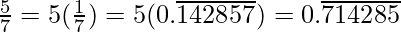
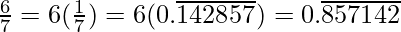
Question 3: Express the following in the form p/q, where p and q are integers and q ≠ 0.

(i)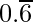 

Solution:

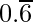= 0.66666……

Lets’s take, x = 0.66666……

10x = 6.666….

So, 

10x – x = (6.6666…..) – (0.66666……..)

9x = 6

x = 6/9 

x = 2/3 

Hence, x is in the form p/q, here p and q are integers and q ≠ 0.

(ii)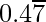 

Solution:

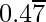 = 0.4777777……

Lets’s take, x = 0.4777777……

10x = 4.77777…….

So,

10x – x = (4.77777…….) – (0.4777777……)

9x = 4.3

9x = 43/10 

x = 43/90

Hence, x is in the form p/q, here p and q are integers and q ≠ 0.

(iii)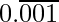 

Solution:

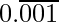 = 0.001001001……

Lets’s take, x = 0.001001001……

1000x = 1.001001001……

So,

1000x – x = (1.001001001……) – (0.001001001……)

999x = 1

x = 1/999

Hence, x is in the form p/q, here p and q are integers and q ≠ 0.

Question 4. Express 0.99999 …. in the form p/q, Are you surprised by your answer? With your teacher and classmates discuss why the answer makes sense.

Solution:

Lets’s take, x = 0.99999……

10x = 9.99999….

So,

10x – x = (9.99999…..) – (0.99999……..)

9x = 9

x = 1

As, 0.9999….. just goes on, then at some point of time there is no gap between 1 and 0.9999….

We can observe that, 0.999 is too much near 1, hence, 1 is justified as the answer.

Hence, x is in the form p/q, where p and q are integers and q ≠ 0.

Question 5. What can the maximum number of digits be in the repeating block of digits in the decimal expansion of 1/17? Perform the division to check your answer.

Solution:

In the given question,

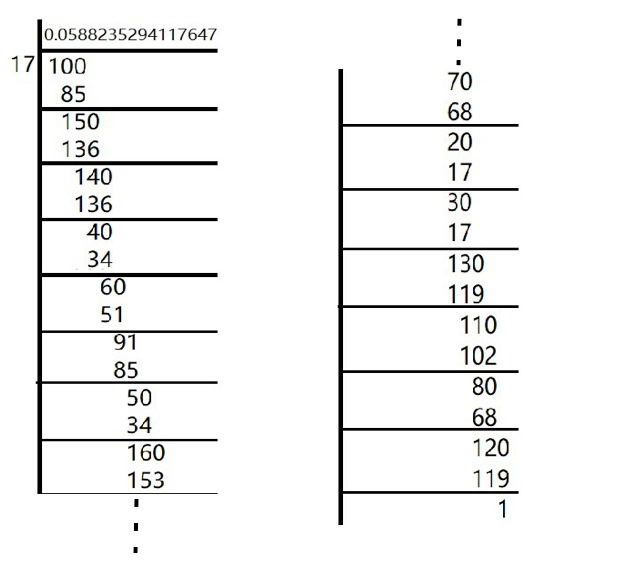
There are 16 digits in the repeating block of the decimal expansion of 1/17

Here, the remainder never becomes zero and remainders repeat after a certain stage.

Hence, decimal expansion is non-terminating recurring

1/17 =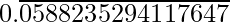 

Question 6. Look at several examples of rational numbers in the form p/q (q ≠ 0), where p and q are integers with no common factors other than 1 and having terminating decimal representations (expansions). Can you guess what property q must satisfy?

Solution:

We observe that when q is 2, 4, 5, 8, 10… Then the decimal expansion is terminating. 

Let’s take some example,

1/2 = 0. 5, denominator q = 2¹

7/8 = 0. 875, denominator q =2³

4/5 = 0. 8, denominator q = 5¹

So, we conclude that terminating decimal may be obtained in the situation where 

prime factorization of the denominator of the given fractions has the power 

of only 2 or only 5 or both.

In the form of 2^m × 5ⁿ, where n, m are natural numbers.

Question 7. Write three numbers whose decimal expansions are non-terminating non-recurring.

Solution:

As we know that all irrational numbers are non-terminating non-recurring. 

So,

√5 = 2.23606798…….

√27 =5.19615242……

√41 = 6.40312424…..

Question 8. Find three different irrational numbers between the rational numbers 5/7 and 9/11.

Solution:

As, decimal expansion of

5/7 =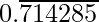 

9/11 =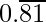 

Hence, three different irrational numbers between them can be as follows,

0.73073007300073000073…

0.75075007300075000075…

0.76076007600076000076…

Question 9. Classify the following numbers as rational or irrational :

(i) √23 

Solution:

√23 = 4.79583152……

As the number is non-terminating non-recurring.

It is an irrational number.

(ii) √225

Solution:

√225 = 15 = 15/1 

As the number can be represented in p/q form, where q ≠ 0.

It is a rational number.

(iii) 0.3796

Solution:

As, the number 0.3796, is terminating.

It is a rational number.

(iv) 7.478478…

Solution:

As, the number 7.478478, is non-terminating but recurring.

It is a rational number.

(v) 1.101001000100001…

Solution:

As, the number 1.101001000100001…, is non-terminating but recurring.

It is a rational number.

Number Systems: Exercise 1.4

Question 1. Visualize 3.765 on the number line, using successive magnification.

Solution:

Now in the given question, you have to represent 3.765 on the number line using the successive magnification method.

Step 1: We will check the range of the number and magnify it accordingly. That is, 3.765 will lie between 3 and 4 so we will magnify the value between 3 and 4.

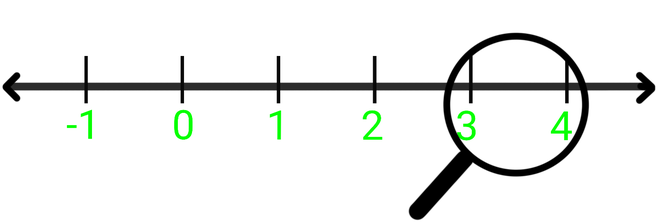
Magnify 3 and 4

Step 2: Now 3.76 will lie between 3.7 and 3.8, so we will magnify the value between 3.7 and 3.8.

Step 3: Now as we will magnify we will check the range, that is, 3.765 will lie between 3.76 and 3.77.

Step 4: Now as we will magnify the value between 3.76 and 3.77 we will find the value 3.765.

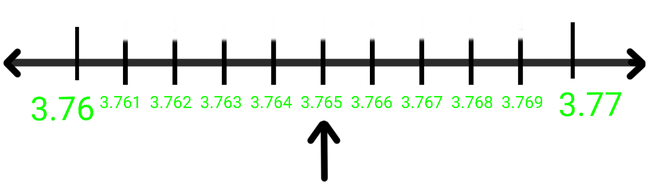
Hence 3.765 is found between 3.76 and 3.77

Question 2. Visualize 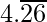 on the number line, up to 4 decimal places.

Solution:

Now in this question, we have to represent the number 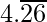 on the number line. The bar sign (   ͞   ) above .26 depicts that the number .26 is repeated continuously after the decimal point.  But it is given that we have to represent the number up to 4 decimal places only, that is, we have to represent 4.2626 on the number line.  

Step 1: We will check the range of the number and magnify it accordingly.  

Step 2: Now 4.2626 will lie between 4 and 5, so we will magnify the value between 4 and 5.

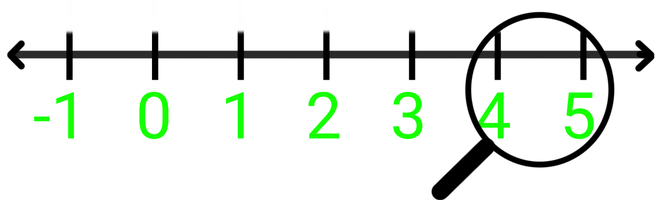
Magnify 4 and 5

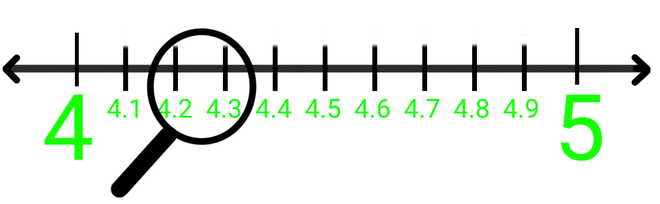
Step 3: 4.26 will lie between 4.2 and 4.3, so we will magnify the value between 4.2 and 4.3.

Step 4: 4.262 will lie between 4.26 and 4.27, so we will magnify the value between 4.26 and 4.27.

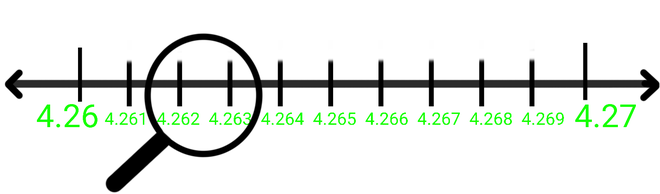
Step 5: Now at last 4.2626 will lie between 4.262 and 4.263, so we will magnify the value between 4.262 and 4.263.

Step 6: As we will magnify the value between 4.262 and 4.263 we will get 4.2626.

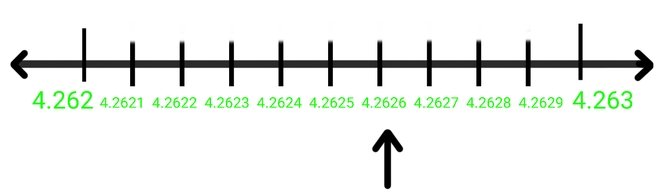
Hence 4.2626 is found between 4.262 and 4.263

Number Systems: Exercise 1.5

Question 1: Classify the following numbers as rational or irrational:

(i) 2 –√5 

(ii) (3 +√23)- √23

(iii) 2√7 / 7√7

(iv) 1/√2

(v) 2π

Solution:

(i) 2 –√5 

As √5 = 2.2360678… which is non-terminating and non-recurring. It is an irrational number.

When we substitute the value of √5 in equation 2 –√5, we get,

2-√5 = 2-2.2360678… 

2-√5 = -0.2360678

Since the number, – 0.2360678…, is a non-terminating and non-recurring,

Therefore, 2 –√5 is an irrational number.

(ii) (3 +√23)- √23

(3 +√23) –√23 = 3+√23–√23

= 3

Since, the number 3 is rational number

Therefore, (3 +√23)- √23 is rational.

(iii) 2√7 / 7√7

2√7 / 7√7 = (2/7)× (√7/√7)

2√7 / 7√7 = (2/7)× (√7/√7) 

= (2/7)×1 [As (√7/√7) = 1]

= 2/7 

Since the number, 2/7 is in p/q form

Therefore, 2√7/7√7 is rational.

(iv) 1/√2

As, √2 = 1.41421… which is non-terminating and non-recurring. It is a rational number.

When we divide 1/√2 we get,

1/√2 = 1/1.41421…

=0.70710…

Since the number, 0.7071..is a non-terminating and non-recurring,

Therefore, 1/√2 is an irrational number.

(v) 2π

The value of π is 3.1415…

When we substitute the value of π in equation 2π, we get,

2π = 2 × 3.1415…  = 6.2831…

Since the number, 6.2831…, is non-terminating non-recurring, 

Therefore, 2π is an irrational number.

Question 2: Simplify each of the following expressions:

(i) (3+√3)(2+√2)

(ii) (3+√3)(3-√3)

(iii) (√5+√2)²

(iv) (√5-√2)(√5+√2)

Solution:

(i) (3+√3)(2+√2)

After opening the brackets, we get, 

(3+√3)(2+√2)= (3×2)+(3×√2)+(√3×2)+(√3×√2)

(3+√3)(2+√2) = 6+3√2+2√3+√6

(ii) (3+√3)(3-√3)

After opening the brackets, we get,

(3+√3)(3-√3) = 3²-(√3)²

= 9-3

(3+√3)(3-√3) = 6

(iii) (√5+√2)²

After opening the brackets, we get,

(√5+√2)² = √5²+(2×√5×√2)+ √2²       [By using the formula (a + b)² = a² + 2ab + b²]

= 5+2×√10+2 

(√5+√2)² = 7+2√10

(iv) (√5-√2)(√5+√2)

After opening the brackets, we get,

(√5-√2)(√5+√2) = (√5²-√2²) 

= 5-2 

= 3

Question 3: Recall, π is defined as the ratio of the circumference (say c) of a circle to its diameter, (say d). That is, π =c/d. This seems to contradict the fact that π is irrational. How will you resolve this contradiction?

Solution:

Given π = c/d = 22/7 which is equal to 3.142… which is non-terminating non-recurring decimal.

Therefore, π is irrational.

Question 4: Represent (√9.3) on the number line.

Solution:

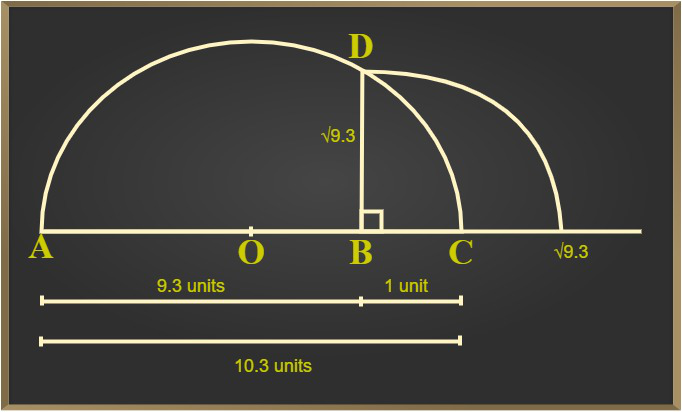
To represent √9.3 on the number line, follow the following steps,

Step 1: Draw a 9.3 units long line segment, name the line as AB. 

Step 2: Extend AB to C such that BC=1 unit.

Step 3: Now, AC = 10.3 units. Let the centre of AC be O.

Step 4: Draw a semi-circle with radius OC and centre O.

Step 5: Draw a BD perpendicular to AC at point B which is intersecting the semicircle at D.

Step 6: Join BD.

Step 7: Taking BD as radius and B as the centre point and draw an arc which touches the line segment. 

The point where it intersects the line segment is at a distance of √9.3 from B as shown in the figure.

Question 5: Rationalize the denominators of the following:

(i) 1/√7  

(ii) 1/(√7-√6)

(iii) 1/(√5+√2)

(iv) 1/(√7-2)

Solution:

(i) 1/√7 

Multiply and divide 1/√7 by √7 we get,

(1×√7)/(√7×√7) = √7/7

= √7/7

(ii) 1/(√7-√6)

Multiply and divide 1/(√7-√6) by (√7+√6) we get,

[1/(√7-√6)]×(√7+√6)/(√7+√6) = (√7+√6)/(√7-√6)(√7+√6)

= (√7+√6)/√7²-√6² [As, (a+b)(a-b) = a²-b²]

= (√7+√6)/(7-6)

= (√7+√6)/1

= √7+√6

(iii) 1/(√5+√2)

Multiply and divide 1/(√5+√2) by (√5-√2) we get,

[1/(√5+√2)]×(√5-√2)/(√5-√2) = (√5-√2)/(√5+√2)(√5-√2)

= (√5-√2)/(√5²-√2²) [As, (a+b)(a-b) = a²-b²]

= (√5-√2)/(5-2)

= (√5-√2)/3

(iv) 1/(√7-2)

Multiply and divide 1/(√7-2) by (√7+2) we get,

1/(√7-2)×(√7+2)/(√7+2) = (√7+2)/(√7-2)(√7+2)

= (√7+2)/(√7²-2²) [As, (a+b)(a-b) = a²-b²]

= (√7+2)/(7-4)

= (√7+2)/3

Number Systems: Exercise 1.6

Question 1. Find the Value of:

(i) 64^1/2

64^1/2

= (8 × 8)^1/2

= (8²)^½

= 8¹

= 8

(ii) 32^1/5

32^1/5

= (2 x 2 x 2 x 2 x 2)^1/5

= (2⁵)^⅕

= 2¹

= 2

(iii) 125^1/3

(125)^1/3

= (5 × 5 × 5)^1/3

= (5³)^⅓

= 5¹

= 5

Question 2. Find the value of:

(i) 9^3/2

9^3/2

= (3 × 3)^3/2

= (3²)^3/2

= 3³

= 27

(ii) 32^2/5

32^2/5

= (2 × 2 × 2 × 2 × 2)^2/5

= (2⁵)^2⁄5

= 2²

= 4

(iii) 16^3/4

16^3/4

= (2 × 2 × 2 × 2)^3/4

= (2⁴)^3⁄4

= 2³

= 8

(iv) 125^-1/3

125^-1/3

= (5 × 5 × 5)^-1/3

= (5³)^-1⁄3

= 5^-1

= 1/5

Question 3. Simplify the followings:

(i) 2^2/3 × 2^1/5

2^2/3 × 2^1/5

= 2^{(2/3) + (1/5)}   ⸪ As, a^m × aⁿ = a^{m + n}

= 2^13/15

(ii) (1/3³)⁷

(1/3³)⁷

= (3^-3)⁷   ⸪ As, (a^m)ⁿ = a^{m x n}

= 3^-21

(iii) 11^1/2/11^1/4

11^1/2/11^1/4

= 11^{(1/2) – (1/4)}    ⸪ As, a^m × a^-n = a^{m – n}

= 11^1/4

(iv) 7^1/2 × 8^1/2

7^1/2 × 8^1/2

= (7 × 8)^1/2  ⸪ As, a^m × b^m = (a × b)^m

= 56^1/2

Important Points to Remember:

• These NCERT solutions are developed by the GfG team, with a focus on students’ benefit.
• These solutions are entirely accurate and can be used by students to prepare for their board exams. 
• Each solution is presented in a step-by-step format with comprehensive explanations of the intermediate steps.

FAQs on NCERT Solutions for Class 9 Maths Chapter 1 – Number Systems

Q1: Why is it important to learn number systems?

Answer:

Since number systems are the cornerstone of mathematics, it is crucial to understand them. In the real world, numbers are employed for quantity representation, measurement, and counting. Numerous mathematical disciplines, including algebra, geometry, and calculus, use number systems to help students organise and comprehend numbers.

Q2: What topics are covered in NCERT Solutions for Class 9 Maths Chapter 1 – Number Systems?

Answer:

NCERT Solutions for Class 9 Maths Chapter 1 – Number Systems covers topics such as the natural numbers, whole numbers, integers, rational numbers, irrational numbers, and real numbers.

Q3: How can NCERT Solutions for Class 10 Maths Class 9 Maths Chapter 1 – Number Systems help me?

Answer:

NCERT Solutions for Class 9 Maths Chapter 1 – Number Systems can help you solve the NCERT exercise without any limitations. If you are stuck on a problem you can find its solution in these solutions and free yourself from the frustration of being stuck on some question.

Q4: How many exercises are there in Class 9 Maths Chapter 1 – Number Systems?

Answer:

There are 6 exercises in the Class 9 Maths Chapter 1 – Number Systems which covers all the important topics and sub-topics.

Q5: Where can I find NCERT Solutions for Class 9 Maths Chapter 1 – Number Systems?

Answer:

You can find these NCERT Solutions in this article created by our team of experts at GeeksforGeeks.