Non-Negative Matrix Factorization
Last Updated :
02 Mar, 2023
Prerequisite : Low Rank Approximation
Non-Negative Matrix Factorization:
Nonnegative Matrix Factorization is a matrix factorization method where we constrain the matrices to be nonnegative. In order to understand NMF, we should clarify the underlying intuition between matrix factorization.
For a matrix A of dimensions m x n, where each element is ≥ 0, NMF can factorize it into two matrices W and H having dimensions m x k and k x n respectively and these two matrices only contain non-negative elements. Here, matrix A is defined as:
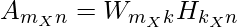
where,
A -> Original Input Matrix (Linear combination of W & H)
W -> Feature Matrix
H -> Coefficient Matrix (Weights associated with W)
k -> Low rank approximation of A (k ≤ min(m,n))
This method is widely used in performing tasks such as feature reduction in Facial Recognition and for various NLP tasks.
Intuition:

Fig 1 : NMF Intuition
The objective of NMF is dimensionality reduction and feature extraction. So, when we set lower dimension as k, the goal of NMF is to find two matrices W ∈ Rm×k and H ∈ Rn×k having only nonnegative elements. (As shown in Fig 1)
Therefore, by using NMF we are able to obtain factorized matrices having significantly lower dimensions than those of the product matrix. Intuitively, NMF assumes that the original input is made of a set of hidden features, represented by each column of W matrix and each column in H matrix represents the ‘coordinates of a data point’ in the matrix W. In simple terms, it contains the weights associated with matrix W.
In this, each data point that is represented as a column in A, can be approximated by an additive combination of the non-negative vectors, which are represented as columns in W.
How Does it Work?
- NMF decomposes multivariate data by creating a user-defined number of features. Each feature is a linear combination of the original attribute set; the coefficients of these linear combinations are non-negative.
- NMF decomposes a data matrix V into the product of two lower rank matrices W and H so that V is approximately equal to W times H.
- NMF uses an iterative procedure to modify the initial values of W and H so that the product approaches V. The procedure terminates when the approximation error converges or the specified number of iterations is reached
- During model apply, an NMF model maps the original data into the new set of attributes (features) discovered by the model.
Real-life example:
Let us consider some real-life examples to understand the working of the NMF algorithm. Let’s take a case of image processing.
Suppose, we have an input image, having pixels that form matrix A. Using NMF, we factorize it into two matrices, one containing the facial feature set [Matrix W] and the other containing the importance of each facial feature in the input image, i.e. the weights [Matrix H]. (As shown in Fig 2.)

Fig 2 : NMF in Image Processing
NMF is used in major applications such as image processing, text mining, spectral data analysis and many more. Currently, there is an ongoing research on NMF to increase its efficiency and robustness. Other research is being done on collective factorization, efficient update of matrices etc. as well. For any doubt/query, comment below.
Share your thoughts in the comments
Please Login to comment...