Prerequisites: Eigen Values and Eigen Vectors
Before getting into the in-depth math behind computations involved with Eigenvectors, let us briefly discuss what an eigenvalue and eigenvector actually are.
Eigenvalue and Eigenvectors:
The word ‘eigen’ means ‘characteristics‘. In general terms, the eigenvalues and eigenvectors give the characteristics of a matrix or a vector.
Eigenvector: It is a vector represented by a matrix X such that when X is multiplied with any matrix A, then the direction of the resultant matrix remains the same as vector X. Observe Fig 1 carefully to look at a graphical representation of an eigenvector.

Fig 1 : Eigenvector representation
In Fig 1, we observe the following scalar transformations:
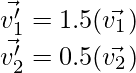
After applying these transformations, the vectors v1‘ and v2‘ are in the same direction as v1 and v2. So as per our definition, these are considered as eigenvectors. But resultant vector v3‘ is not in the same direction as v3. Hence it cannot be considered as a eigenvector.
Eigenvalues: It tells us about the extent to which the eigenvector has been stretched or diminished.
In the above case, the eigenvalues will be 1.5 and 0.5.
Computing Eigenvectors
We can calculate eigenvalues of any matrix using the characteristic equation of the matrix (as discussed in the prerequisite article) that is:
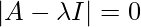
The roots of the above equation (i.e. values of λ) gives us the eigenvalues.
Using the values of λ obtained, we can find the corresponding eigenvectors using the equation given below.
![Rendered by QuickLaTeX.com At\ \lambda=i\\ [A-iI ]X_i = 0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-517eda28572cf234c4db93718dadbc4b_l3.png)
Example Problem
Consider the following example for a better understanding. Let there be a 3×3 matrix X defined as:
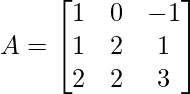
Find the eigen values and eigen vectors corresponding to the matrix A.
Solution
1. Finding the eigen values.
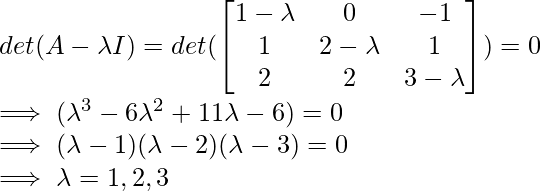
Thus, the eigen values obtained are 1, 2 and 3.
2. Finding the eigen vectors.
Using the formula given above, we will calculate a corresponding eigen vector xi for each value of λi.
![Rendered by QuickLaTeX.com At\ \lambda = 1 \\ [A - (1)I]X_1 = 0 \\ \implies \begin{bmatrix} 1-1 & 0 & -1\\1 & 2-1 & 1\\2 & 2 & 3-1 \end{bmatrix} \begin{bmatrix} x_1\\x_2\\x_3 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix} \\ \implies \begin{bmatrix} 0 & 0 & -1\\1 & 1 & 1\\2 & 2 & 2 \end{bmatrix} \begin{bmatrix} x_1\\x_2\\x_3 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix} \\ On\ solving,\ we\ get\ the\ following\ equations: \\ x_3 = 0 (x_1) \\ x_1 + x_2 = 0 \implies x_2 = -x_1 \\ \therefore X_1 = \begin{bmatrix} x_1\\-x_1\\ 0(x_1) \end{bmatrix} \\ \implies X_1 = \begin{bmatrix} 1\\-1\\0 \end{bmatrix}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0c193cf360ae6215adeb493a0f425284_l3.png)
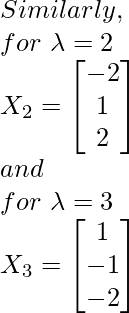
Thus, we obtain the eigen vectors X1, X2, X3 corresponding to each value of λ.
Rank of a matrix:
Rank of a (m x n) matrix is determined by the number of linearly independent rows present in the matrix. Consider the example given below for a better understanding.
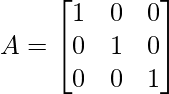
All 3 rows of matrix A are linearly independent. Therefore, Rank ( A ) = 3.
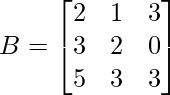
Rank ( B ) = 2. This is because Row 3 is dependent on R1 and R2. [R3 <- R1 + R2]
Some important properties:
For any matrix A of shape m x n, the following rank properties are applicable:
- Rank (A) = Rank (AT)
- Rank (BAC) = Rank (A) provided B and C are invertible matrices.
- Rank (AB) ≤ min{ Rank (A) + Rank (B) }
Before getting into Low-Rank Approximation, it is important to understand the following:
Any matrix A of shape m x n having rank (A) = r is said to be factorized when it takes the form:
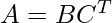
where, the shapes of the matrices are:
mat(A) -> m x n
mat(B) -> m x r
mat(C) -> n x r
We say that matrix A has a low rank if r << min {m,n}.
Low Rank Approximation (LRA)
Based on the above two discussed method, we define LRA as:
For a matrix A of shape m x n and rank (A) << min {m, n}, the low-rank approximation of A is to find another matrix B such that rank (B) ≤ rank (A). Intuitively, we tend to see how linearly similar matrix B is to the input matrix A. Mathematically, LRA is a minimization problem, in which we measure the fit between a given matrix (the data) and an approximating matrix (the optimization variable).
Motivation for LRA
Let us assume 3 matrices X, Y, Z of dimensions (50 x 40), (50 x 10), (40 x 10) respectively where rank(X) = 10. Therefore, as per matrix factorization, the three matrices are of the form A = BCT. We observe that:
Amxn = BmxrCTrxn
No of elements/pixels in mat(A) = (50 x 40) = 2000
while
No of elements/pixels in mat(BCT) = (50 x 10) + (10 x 40) = 900.
Thus, by using low-rank approximation, we can reduce the number of pixels of input data by a significant amount. (1100 fewer pixels than input image in the above case)
Application of LRA
This method is commonly used in Image Processing tasks where the input image (data) is very large and needs to be compressed before any processing task. Observe the two images of the same person given below.

After LRA image vs Input image
After applying LRA, we are able to obtain an image that is very similar to the original image by discarding some unimportant pixels, hence reducing the size of the image as well. After doing this, it becomes much easier to handle such large datasets and perform a variety of pre-processing tasks on them.
Eigenvalue and eigenvector computation is a fundamental problem in linear algebra with numerous applications in various fields, including machine learning, signal processing, and quantum mechanics, among others. Given a square matrix A, an eigenvector v is a non-zero vector that satisfies the equation Av = λv, where λ is a scalar known as the eigenvalue corresponding to v.
To compute eigenvectors, we typically use numerical algorithms that involve iterative methods, such as the power method or the inverse power method. These methods can efficiently compute the eigenvectors associated with the largest or smallest eigenvalues of a matrix, respectively. Additionally, there are also methods that can compute all the eigenvectors of a matrix simultaneously, such as the QR algorithm or the Jacobi method.
Low-rank approximations are a commonly used technique in data analysis and machine learning for reducing the dimensionality of high-dimensional data. Given a matrix A, a low-rank approximation involves finding a matrix B that is of lower rank than A but approximates A as closely as possible. This is typically done by finding the truncated singular value decomposition (SVD) of A, which provides a low-rank approximation of A by keeping only the largest singular values and corresponding singular vectors.
Low-rank approximations can be computed using various numerical algorithms, including the randomized SVD and the alternating least squares (ALS) algorithm. These methods are particularly useful for handling large-scale datasets that are difficult to store or process in their original high-dimensional form.
Advantages of Eigenvector Computation:
Eigenvectors provide a concise representation of a matrix, as they capture the most important features of the matrix.
Eigenvectors can be used to solve linear systems of equations, which arise in many practical applications.
Eigenvectors can be used to diagonalize a matrix, which simplifies many computations and allows us to easily compute powers and exponentials of the matrix.
Disadvantages of Eigenvector Computation:
Eigenvector computation can be computationally expensive, particularly for large matrices.
Eigenvectors may not exist for all matrices, or they may be complex numbers.
Eigenvectors may not be unique, as a matrix may have multiple eigenvectors corresponding to the same eigenvalue.
Advantages of Low-Rank Approximations:
Low-rank approximations can significantly reduce the dimensionality of high-dimensional data, making it easier to store and process.
Low-rank approximations can reduce noise and remove irrelevant features, improving the accuracy of data analysis and machine learning models.
Low-rank approximations can be computed efficiently using numerical algorithms, particularly for large datasets.
Disadvantages of Low-Rank Approximations:
Low-rank approximations may not capture all the information in the original high-dimensional data, leading to some loss of information.
Choosing an appropriate rank for the low-rank approximation can be challenging, and different choices can lead to different results.
Low-rank approximations may not work well for all types of data, particularly if the data is highly irregular or has a complex structure.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...