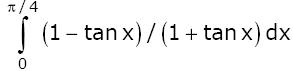Numerical Methods and Calculus
Question 1
Which one of the following functions is continuous at x = 3?
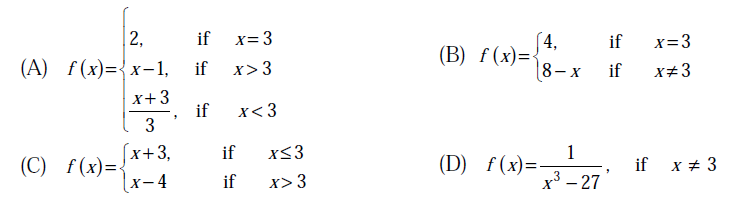 [/caption]
[/caption]
Question 3
Consider the function f(x) = sin(x) in the interval [π/4, 7π/4]. The number and location(s) of the local minima of this function are
Question 4
The bisection method is applied to compute a zero of the function f(x) = x4 – x3 – x2 – 4 in the
interval [1,9]. The method converges to a solution after ––––– iterations
Question 5
Given i=√-1, what will be the evaluation of the integral [Tex]\\int_{0}^{\\pi/2} \\frac{\\cos x + i\\sin x}{\\cos x - i\\sin x} dx [/Tex]?
Question 6
Newton-Raphson method is used to compute a root of the equation x2-13=0 with 3.5 as the initial value. The approximation after one iteration is
Question 8
Two alternative packages A and B are available for processing a database having 10k records. Package A requires 0.0001n2 time units and package B requires 10nlog10n time units to process n records. What is the smallest value of k for which package B will be preferred over A?
There are 93 questions to complete.