Mathematics | Euler and Hamiltonian Paths
Last Updated :
11 Oct, 2021
Prerequisite – Graph Theory Basics
Certain graph problems deal with finding a path between two vertices such that each edge is traversed exactly once, or finding a path between two vertices while visiting each vertex exactly once. These paths are better known as Euler path and Hamiltonian path respectively.
The Euler path problem was first proposed in the 1700’s.
Euler paths and circuits :
- An Euler path is a path that uses every edge of a graph exactly once.
- An Euler circuit is a circuit that uses every edge of a graph exactly once.
- An Euler path starts and ends at different vertices.
- An Euler circuit starts and ends at the same vertex.
The Konigsberg bridge problem’s graphical representation :

There are simple criteria for determining whether a multigraph has a Euler path or a Euler circuit. For any multigraph to have a Euler circuit, all the degrees of the vertices must be even.
Theorem – “A connected multigraph (and simple graph) with at least two vertices has a Euler circuit if and only if each of its vertices has an even degree.”
Proof of the above statement is that every time a circuit passes through a vertex, it adds twice to its degree. Since it is a circuit, it starts and ends at the same vertex, which makes it contribute one degree when the circuit starts and one when it ends. In this way, every vertex has an even degree.
Since the konigsberg graph has vertices having odd degrees, a Euler circuit does not exist in the graph.
Theorem – “A connected multigraph (and simple graph) has an Euler path but not an Euler circuit if and only if it has exactly two vertices of odd degree.”
The proof is an extension of the proof given above. Since a path may start and end at different vertices, the vertices where the path starts and ends are allowed to have odd degrees.
- Example – Which graphs shown below have an Euler path or Euler circuit?

- Solution –
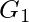 has two vertices of odd degree
has two vertices of odd degree 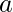 and
and 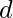 and the rest of them have even degree. So this graph has an Euler path but not an Euler circuit. The path starts and ends at the vertices of odd degree. The path is-
and the rest of them have even degree. So this graph has an Euler path but not an Euler circuit. The path starts and ends at the vertices of odd degree. The path is- 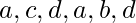 .
.
 has four vertices all of even degree, so it has a Euler circuit. The circuit is –
has four vertices all of even degree, so it has a Euler circuit. The circuit is – 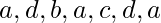 .
.
Hamiltonian paths and circuits :
Hamiltonian Path – A simple path in a graph 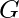 that passes through every vertex exactly once is called a Hamiltonian path.
that passes through every vertex exactly once is called a Hamiltonian path.
Hamiltonian Circuit – A simple circuit in a graph 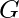 that passes through every vertex exactly once is called a Hamiltonian circuit.
that passes through every vertex exactly once is called a Hamiltonian circuit.
Unlike Euler paths and circuits, there is no simple necessary and sufficient criteria to determine if there are any Hamiltonian paths or circuits in a graph. But there are certain criteria which rule out the existence of a Hamiltonian circuit in a graph, such as- if there is a vertex of degree one in a graph then it is impossible for it to have a Hamiltonian circuit.
There are certain theorems which give sufficient but not necessary conditions for the existence of Hamiltonian graphs.
Dirac’s Theorem- “If 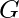 is a simple graph with
is a simple graph with 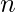 vertices with
vertices with  such that the degree of every vertex in
such that the degree of every vertex in 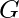 is at least
is at least 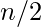 , then
, then 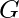 has a Hamiltonian circuit.”
has a Hamiltonian circuit.”
Ore’s Theorem- “If 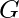 is a simple graph with
is a simple graph with 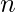 vertices with
vertices with  such that
such that 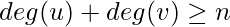 for every pair of non-adjacent vertices
for every pair of non-adjacent vertices 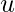 and
and  in
in 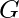 , then
, then 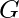 has a Hamiltonian circuit.”
has a Hamiltonian circuit.”
As mentioned above that the above theorems are sufficient but not necessary conditions for the existence of a Hamiltonian circuit in a graph, there are certain graphs which have a Hamiltonian circuit but do not follow the conditions in the above-mentioned theorem. For example, the cycle 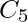 has a Hamiltonian circuit but does not follow the theorems.
has a Hamiltonian circuit but does not follow the theorems.
Note: Kn is Hamiltonian circuit for 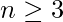
There are many practical problems which can be solved by finding the optimal Hamiltonian circuit. One such problem is the Travelling Salesman Problem which asks for the shortest route through a set of cities.
- Example 1- Does the following graph have a Hamiltonian Circuit?

- Solution- Yes, the above graph has a Hamiltonian circuit. The solution is –

- Example 2- Does the following graph have a Hamiltonian Circuit?

- Solution- No the above graph does not have a Hamiltonian circuit as there are two vertices with degree one in the graph.
GATE CS Corner Questions
Practicing the following questions will help you test your knowledge. All questions have been asked in GATE in previous years or in GATE Mock Tests. It is highly recommended that you practice them.
1. GATE CS 2007, Question 23
2. GATE CS 2005, Question 84
3. GATE CS 2008, Question 26
References-
Eulerian path – Wikipedia
Hamiltonian path – Wikipedia
Discrete Mathematics and its Applications, by Kenneth H Rosen
Share your thoughts in the comments
Please Login to comment...