Mathematics | Graph Theory Basics – Set 1
Last Updated :
05 Oct, 2023
A graph is a data structure that is defined by two components :
- A node or a vertex.
- An edge E or ordered pair is a connection between two nodes u,v that is identified by unique pair(u,v). The pair (u,v) is ordered because (u,v) is not same as (v,u) in case of directed graph.The edge may have a weight or is set to one in case of unweighted graph.
Consider the given below graph, 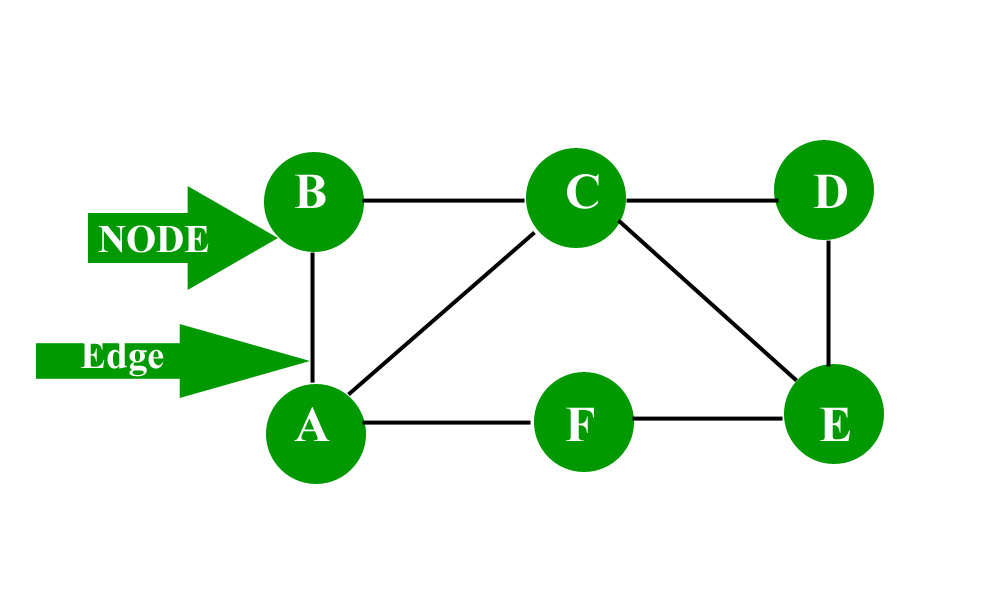 To know about “Graph representation” click here
To know about “Graph representation” click here
Applications: Graph is a data structure which is used extensively in our real-life.
- Social Network: Each user is represented as a node and all their activities,suggestion and friend list are represented as an edge between the nodes.
- Google Maps: Various locations are represented as vertices or nodes and the roads are represented as edges and graph theory is used to find shortest path between two nodes.
- Recommendations on e-commerce websites: The “Recommendations for you” section on various e-commerce websites uses graph theory to recommend items of similar type to user’s choice.
- Graph theory is also used to study molecules in chemistry and physics.
More on graphs: Characteristics of graphs:
- Adjacent node: A node ‘v’ is said to be adjacent node of node ‘u’ if and only if there exists an edge between ‘u’ and ‘v’.
- Degree of a node: In an undirected graph the number of nodes incident on a node is the degree of the node. In case of directed graph ,Indegree of the node is the number of arriving edges to a node. Outdegree of the node is the number of departing edges to a node.
Note: 1 a self-loop is counted twice
2 the sum of degree of all the vertices in a graph G is even.

- Path: A path of length ‘n’ from node ‘u’ to node ‘v’ is defined as sequence of n+1 nodes.
P(u,v)=(v0,v1,v2,v3…….vn)
- A path is simple if all the nodes are distinct,exception is source and destination are same.
- Isolated node: A node with degree 0 is known as isolated node.Isolated node can be found by Breadth first search(BFS). It finds its application in LAN network in finding whether a system is connected or not.
Types of graphs: 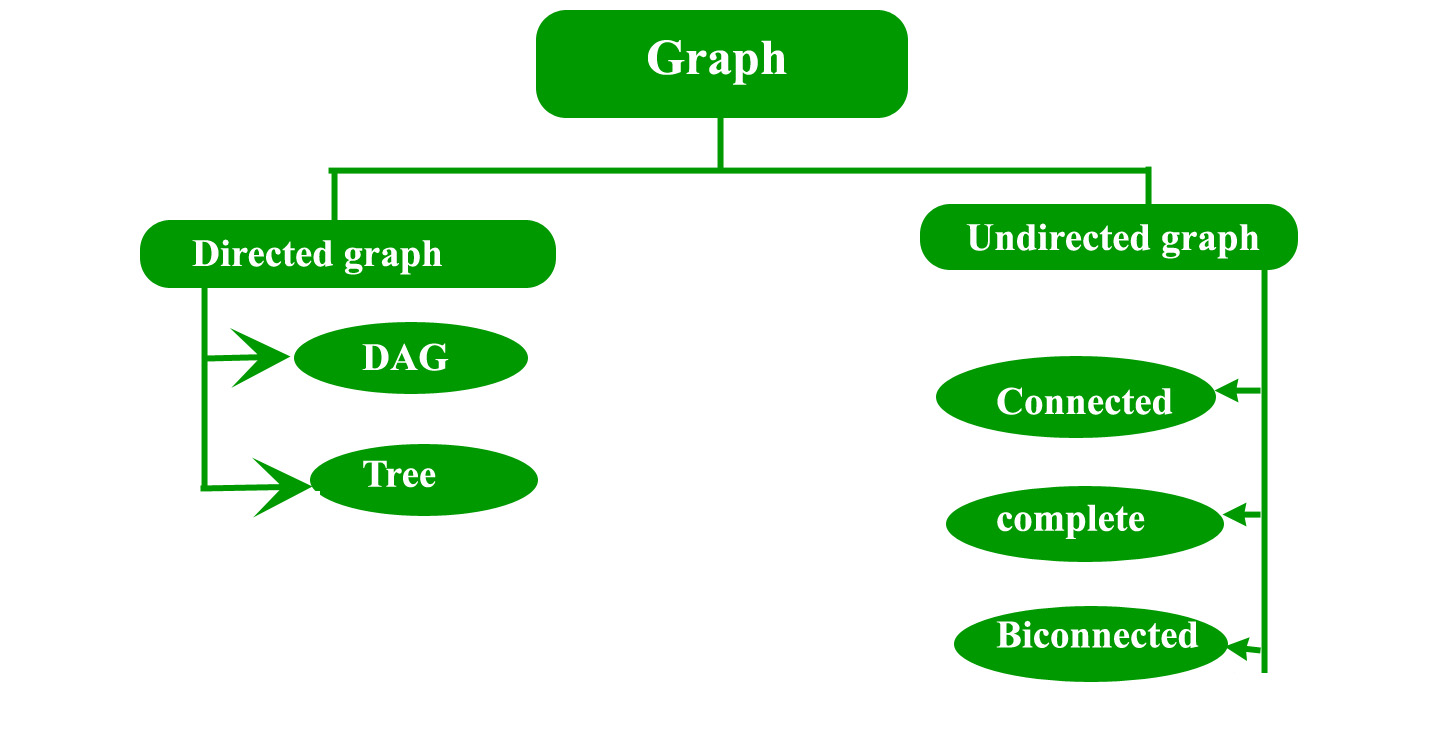
- Directed graph: A graph in which the direction of the edge is defined to a particular node is a directed graph.
- Directed Acyclic graph: It is a directed graph with no cycle.For a vertex ‘v’ in DAG there is no directed edge starting and ending with vertex ‘v’. a) Application :Critical game analysis,expression tree evaluation,game evaluation.
- Tree: A tree is just a restricted form of graph.That is, it is a DAG with a restriction that a child can have only one parent.
- Undirected graph: A graph in which the direction of the edge is not defined.So if an edge exists between node ‘u’ and ‘v’,then there is a path from node ‘u’ to ‘v’ and vice versa.
- Connected graph: A graph is connected when there is a path between every pair of vertices.In a connected graph there is no unreachable node.
- Complete graph: A graph in which each pair of graph vertices is connected by an edge.In other words,every node ‘u’ is adjacent to every other node ‘v’ in graph ‘G’.A complete graph would have n(n-1)/2 edges.See below for proof.
- Biconnected graph: A connected graph which cannot be broken down into any further pieces by deletion of any vertex.It is a graph with no articulation point.
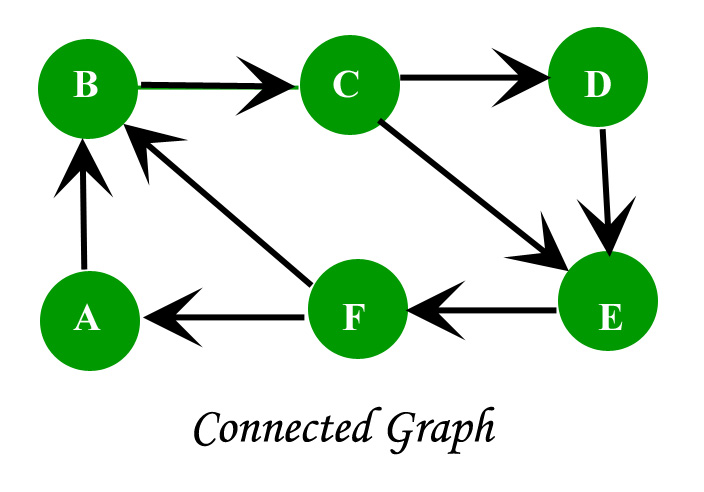
Proof for complete graph:
- Consider a complete graph with n nodes. Each node is connected to other n-1 nodes. Thus it becomes n * (n-1) edges. But this counts each edge twice because this is a undirected graph so divide it by 2.
- Thus it becomes n(n-1)/2.
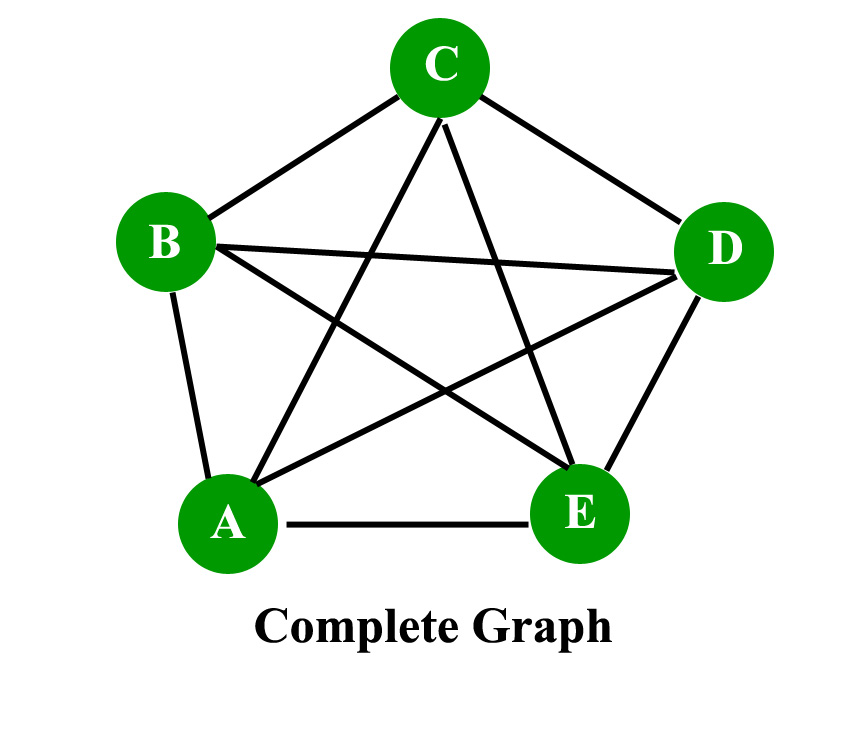 Consider the given graph, //Omit the repetitive edges Edges on node A = (A,B),(A,C),(A,E),(A,C). Edges on node B = (B,C),(B,D),(B,E). Edges on node C = (C,D),(C,E). Edges on node D = (D,E). Edges on node E = EMPTY.https://en.wikipedia.org/wiki/Graph_theory Total edges = 4+3+2+1+0=10 edges. Number of node = 5. Thus n(n-1)/2=10 edges. Thus proven. Read next set – Graph Theory Basics
Consider the given graph, //Omit the repetitive edges Edges on node A = (A,B),(A,C),(A,E),(A,C). Edges on node B = (B,C),(B,D),(B,E). Edges on node C = (C,D),(C,E). Edges on node D = (D,E). Edges on node E = EMPTY.https://en.wikipedia.org/wiki/Graph_theory Total edges = 4+3+2+1+0=10 edges. Number of node = 5. Thus n(n-1)/2=10 edges. Thus proven. Read next set – Graph Theory Basics
Some more graphs :
1. Regular graph :A graph in which every vertex x has same/equal degree.k-regular graph means every vertex has k degree.
Every complete graph Kn will have (n-1)-regular graph which means degree is n-1.

Regular graphs
2. Bipartite graph : It is graph G in which vertex set can be partitioned into two subsets U and V such that each edge of G has one end in U and another end point in V.

Bipartite graph
3. Complete Bipartite graph : it is a simple graph with vertex set partitioned into two subsets : U={v1,v2………..vm} and W={w1,w2,………..wn}
i. There is an edge from each vi to each wj.
ii. there is not self loop.

Complete Bipartite graph
4. Cycle graph : A graph of n vertices (n≥3) . v1,v2,………………..vn with edges (v1,v2),(v2,v3),………..,(vn-1,vn),(vn,v1).

Cycle graph
Share your thoughts in the comments
Please Login to comment...