Number of Boolean functions
Last Updated :
25 Nov, 2019
In the below article, we are going to find the number of
Boolean Functions possible from the given sets of binary number.
Statement-1:
Suppose two sets are set ‘A’ = {1, 2, 3, 4, …….., n} where each number will be either ‘0’ or ‘1’ and hence the total number of boolean variable possible will be
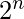
and set ‘B’ = {0, 1}. Now the number of possible boolean function when counting is done from set ‘A’ to ‘B’ will be
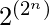
.
Explanation:
As we know that boolean variable is either ‘0’ or ‘1’ and in the set ‘A’ there are ‘n’ numbers and each number will be either ‘0’ or ‘1’ and hence the total number of possible boolean variable are
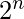
. Now set ‘A’ contain
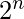
boolean variable and set ‘B’ contain 2 boolean variable.
This can be understood with help of below diagram:

Each element of set ‘A’ makes a function with each element of set ‘B’ hence one element of set ‘A’ makes two function with set ‘B’ and hence total number of possible boolean functions are
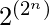
where
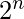
is the number of element in set ‘A’.
Statement-2:
Suppose two sets of ternary variable are set ‘A’ = {1, 2, 3, 4, …….., n} where each number will be either ‘0’ or ‘1’ or ‘2’ and hence the total number of ternary variable possible will be
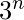
and set ‘B’ = {0, 1}. Now the number of possible boolean function when counting is done from set ‘A’ to ‘B’ will be
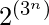
.
Explanation:
As we know that ternary variables are ‘0’ or ‘1’ or ‘2’ and in the set ‘A’ there are ‘n’ numbers and each number will be either ‘0’ or ‘1’ or ‘2’ and hence the total number of possible ternary variables are
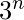
. Now set ‘A’ contain
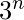
ternary numbers and set ‘B’ contain 2 boolean variable.
This can be understood with help of below diagram:

Each element of set ‘A’ makes a function with each element of set ‘B’ hence one element of set ‘A’ makes two functions with set ‘B’ and hence the total number of possible boolean functions are
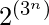
where
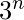
is the number of elements in set ‘A’.
Note:
Similarly for a set ‘A’ of ‘n’ numbers of k-ary variable and set ‘B’ of p-ary variable then the total number of p-ary possible function will be 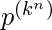 .
.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...